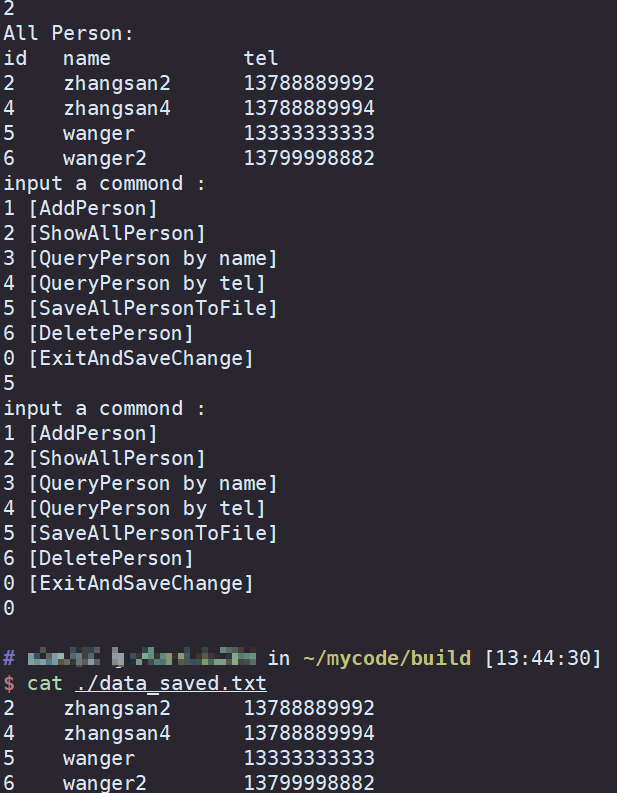
回溯法
适用于:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等
回溯法解决的问题都可以抽象为树形结构,所有回溯法的问题都可以抽象为树形结构!
因为回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
既然是树形结构,遍历树形结构一定要有终止条件,所以回溯也有要终止条件。
什么时候达到了终止条件,树中就可以看出,一般来说搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
回溯法一般是在集合中递归搜索,集合的大小构成了树的宽度,递归的深度构成的树的深度。

for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
可以从图中看出for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了
模板:
回溯算法中函数返回值一般为void
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
例题1:组合
点击跳转

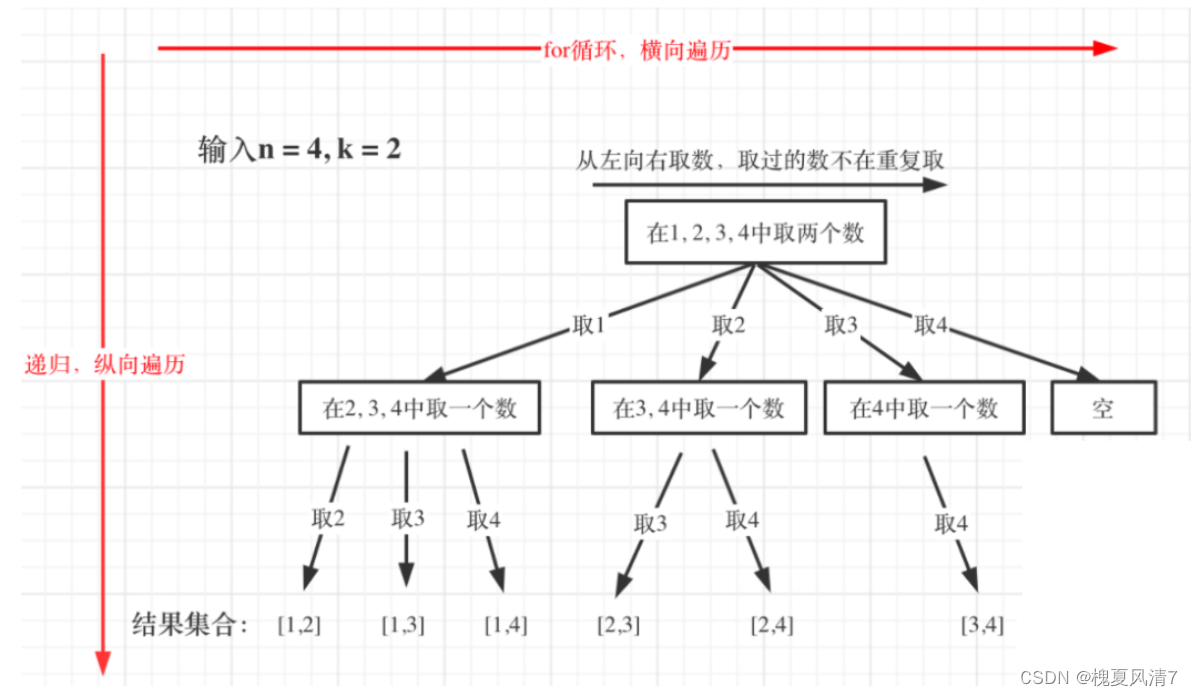
回溯法图解
class Solution {
vector<vector<int>> ret;// 存放符合条件结果的集合
vector<int> path;// 用来存放符合条件单一结果
void banktracking(int n,int k,int startindex)
{
if(path.size()==k) //回溯函数终止条件,path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是 根节点到叶子节点的路径。
{
ret.push_back(path);
return ;
}
for(int i=startindex;i<=n;++i) //单层搜索的过程
{
path.push_back(i); //处理
banktracking(n,k,i+1); //递归
path.pop_back();// 回溯,撤销处理的节点
}
return ;
}
public:
vector<vector<int>> combine(int n, int k) {
path.clear();
ret.clear();
banktracking(n,k,1);
return ret;
}
};
例题2:求数组的全排列并打印出来
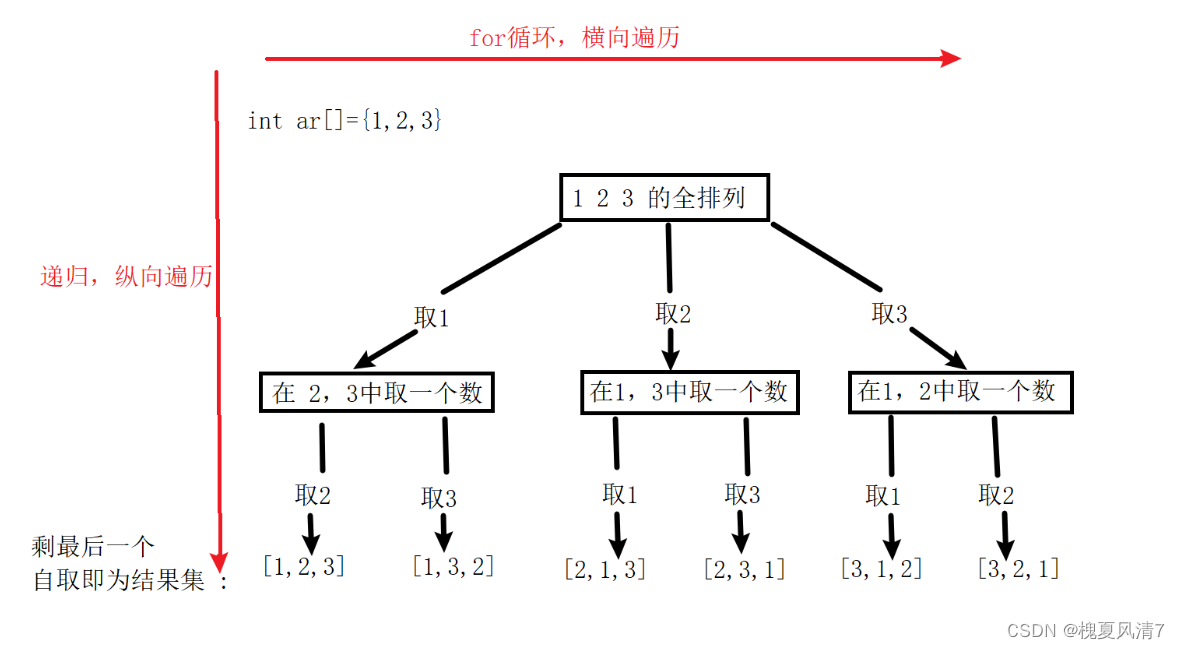
回溯法图解
代码:
void Showar(vector<int> ar)
{
for (auto x: ar)
{
cout << x << " ";
}
cout << endl;
}
void Backtracking(vector<int> ar, int left,int right)
{
if (right == left) //回溯函数终止条件,剩余一个数据,自取后即为全排列
{
Showar(ar); //打印全排列
return;
}
for (int i = left; i < right; ++i)
{
std::swap(ar[left], ar[i]); //处理当前节点(取出操作)
Backtracking(ar, left+1, right); //递归
std::swap(ar[left], ar[i]); //回溯,撤销处理的节点
}
}
int main()
{
vector<int> ar = { 1,2,3};
int n = ar.size();
Backtracking(ar, 0,n) ;
return 0;
}