Titile: 海量数据场景下的热门算法题
从40个亿中产生一个不存在的整数
题目要求:给定一个输入文件,包含40亿个非负整数,请设计一个算法,产生一个不存在该文件中的整数,假设你有1GB的内存来完成这项任务。
- 进阶:如果只有10MB的内存可用,该怎么办
位图存储大数据的原理
假设用哈希表来保存出现过的数,如果 40 亿个数都不同,则哈希表的记录数为 40 亿条,存一个 32 位整数需要 4B,所以最差情况下需要 40 亿 * 4B = 160 亿字节,大约需要16GB 的空间,这是不符合要求的。
40 亿 * 4B = 160 亿字节,大约需要16GB
40 亿 / 8 字节 = 5亿字节,大约 0.5GB 的数组就可以存下 40亿 个
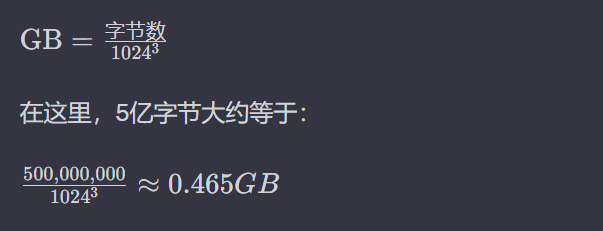
我们申请一个 40亿 的 bitArray 然后直接遍历这里的数据,假如遍历到了 1000 那么就找到 bitArray [1000 - 1] = 1 ,以此类推直到完成最后一个数字的遍历。之后进行第二次的遍历这个 bitArray 循环找到值为 0 的位置这个位置对应的 index + 1 就是不存在的整数
只有10MB来存储
只有 10MB 此时位图也失效了,因为类图最小需要大约 0.5GB 的内存才能进行处理先关的数据
此时就可以尝试使用分块思想,时间换空间,通过两次遍历来搞定
那么如何分块,分多少快才合理?
首先,我们要先大概估算一下,0.5G 大概是 500MB 所以只有 10MB 可以使用我们至少需要分为 50 块。但是我们一般分块都是 2 的倍数 当我们分成 64块的时候那么此时正好每一块大概是 8MB 那么这个就很合理当让如果我们如果分成 128块、256块也是完全问题的
那么我们这里就假设分成 64块进行处理
- 第 0 区间:(0 ~ 67 108 863)
- 第 1 区间(67 108 864~134 217 728)
- 第 i 区间(67 108 864^i ~ 67 108 864^(i + 1) - 1)
- …
- 第 63 区间(4 227 858 432 ~ 4 294 967 295)。
第一次遍历,首先我们创建一个整型数组 countArr[0…63],使用 countArr[i] 用来统计区间 i 上的数有多少。然后使用当前的数字 i 和 67108864 进行取整操作,如果是 0 的话那么就是 第 0 区间上的值,如果是 12 那么还是第 0 区间的值进行countArr[0]++,那么这样的操作之后我们找到自己需要的 0 ~ 67 108 863 的数据的总共的大小,如果大小和 67108864 一样那么就证明这个区间里面没有一个所谓的 不存在的值 。
何时需要第二次遍历? 当然是对应的数据的长度小于 67108864 我们进行第二次的遍历
下面的步骤和第一个解法就有异曲同工直之妙了
- 申请长度为 67 108 864 的 bit map,这占用大约 8MB 的空间,记为 bitArr[0…67108863]。
- 遍历这 40 亿个数,此时的遍历只关注落在第 37 区间上的数,记为 num(num满足num/67 108 864==37),其他区间的数全部忽略。
- 如果步骤 2 的 num 在第 37 区间上,将 bitArr[num - 67108864*37]的值设置为 1,也就是只做第 37 区间上的数的 bitArr 映射。
- 遍历完 40 亿个数之后,在 bitArr 上必然存在没被设置成 1 的位置,假设第 i 个位置上的值没设置成 1,那么 67 108 864´37+i 这个数就是一个没出现过的数。