5 . 最长回文子串（中等）

方法：中心扩散法

思想

• 「中心扩散法」的基本思想是：遍历每一个下标，以这个下标为中心，利用「回文串」中心对称的特点，往两边扩散，看最多能扩散多远。

• 枚举「中心位置」时间复杂度为 O(N)，从「中心位置」扩散得到「回文子串」的时间复杂度为 O(N)，因此时间复杂度可以降到 O(N²) 。

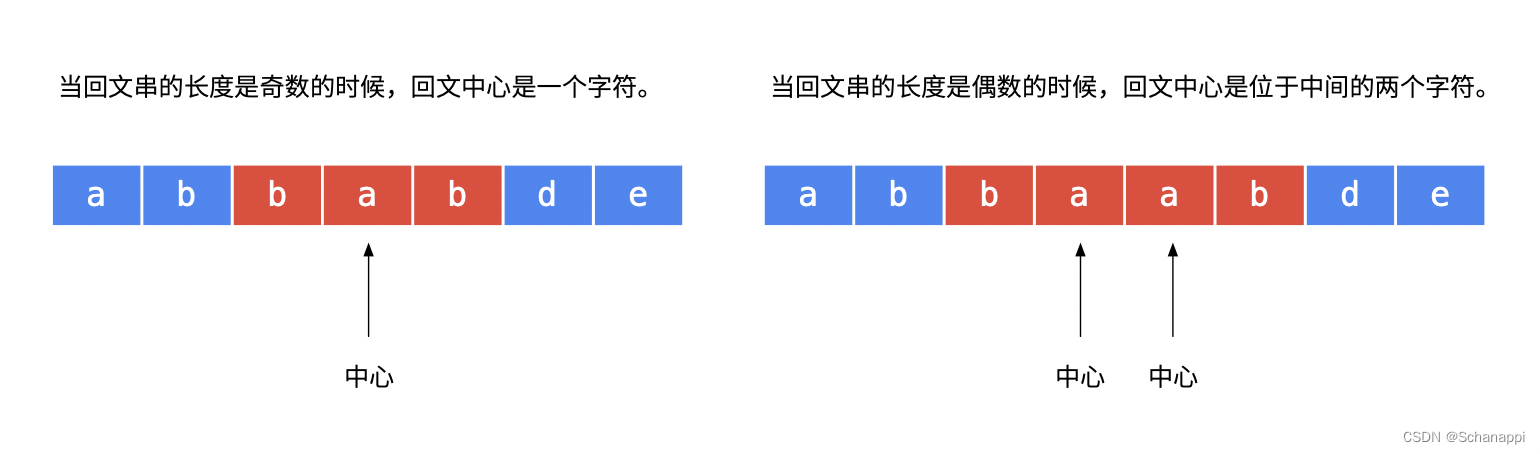
• 细节：回文串在长度为奇数和偶数的时候，「回文中心」的形态不一样：

  • 奇数回文串的「中心」是一个具体的字符，例如：回文串 “aba” 的中心是字符 “b”；
  • 偶数回文串的「中心」是位于中间的两个字符的「空隙」，例如：回文串 “abba” 的中心是两个 “b”，也可以看成两个 “b” 中间的空隙。

  

代码

class Solution {
public:
    int center = 0;
    int len = 0;
    string longestPalindrome(string s) {
        for(int i=0; i<s.size(); ++i) {
            search(i, i, s);
            search(i, i+1, s);
        }
        // 计算最长子串的起始位置
        int begin = center - (len - 1) / 2;
        return s.substr(begin, len);
    }
    void search(int i, int j, string s) {
        if(i < 0 || j >= s.size())    return ;
        // 保存当前中心
        int pos = i;
        while(i >= 0 && j < s.size() && s[i] == s[j]) {
            i--;
            j++;
        }
        // 标记最长的回文子串长度及其中心
        if(j - i - 1 > len) {
            len = j - i - 1;
            center = pos;
        } 
    }
};

参考资料

1. 动态规划、中心扩散、Manacher 算法