查找
假设有如下这样一个有序链表:

想要查找 24、43、59,按照顺序遍历,分别需要比较的次数为 2、4、6
目前查找的时间复杂度是 O(N),如何提高查找效率?
很容易想到二分查找,将查找的时间复杂度降到 O(LogN)
具体来说,我们把链表中的一些节点提取出来,作为索引,类似于二叉搜索树,得到如下结构:
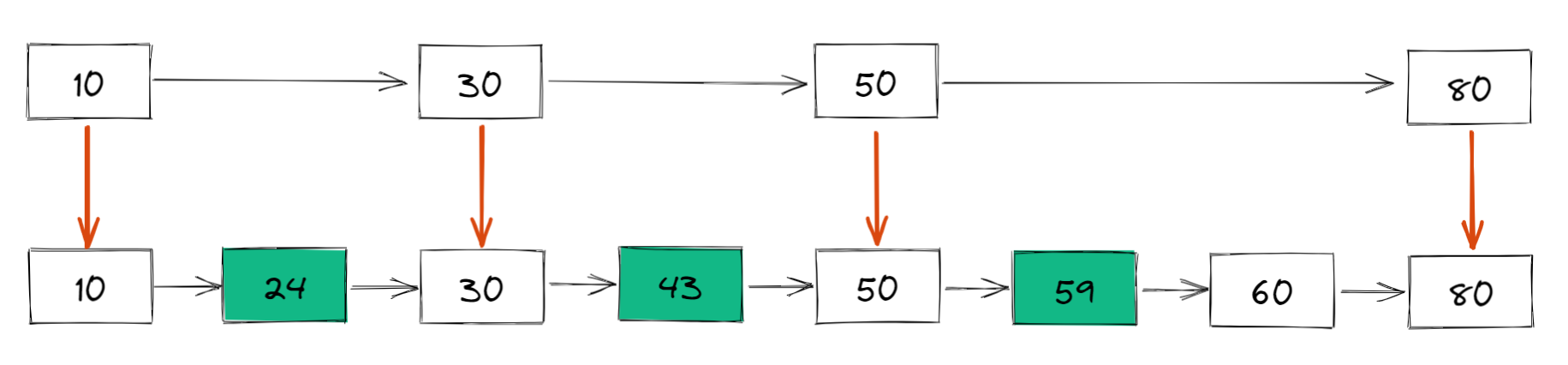
这里我们把 10、30、50、80 提取出来作为一级索引,这样搜索的时候就可以使用二分查找来减少比较次数了。
我们还可以再从一级索引提取一些元素出来,作为二级索引,变成如下结构:
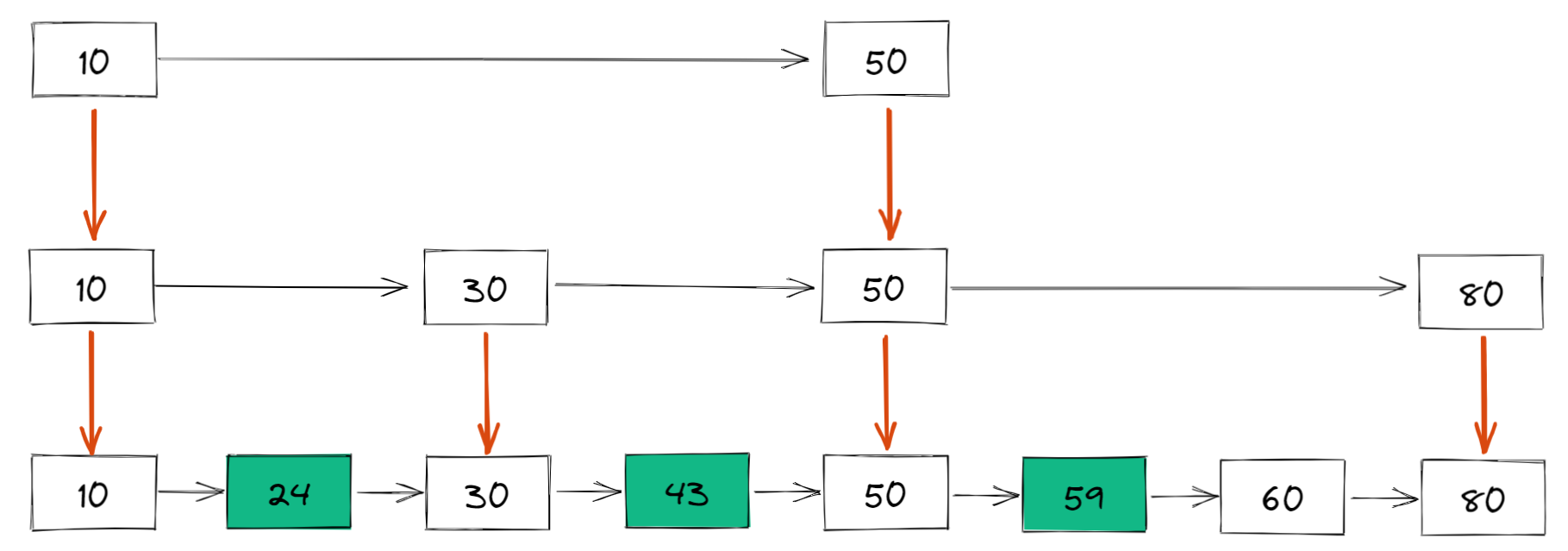
比如如果想要查找 59,那么搜索路径就是下面这样的:
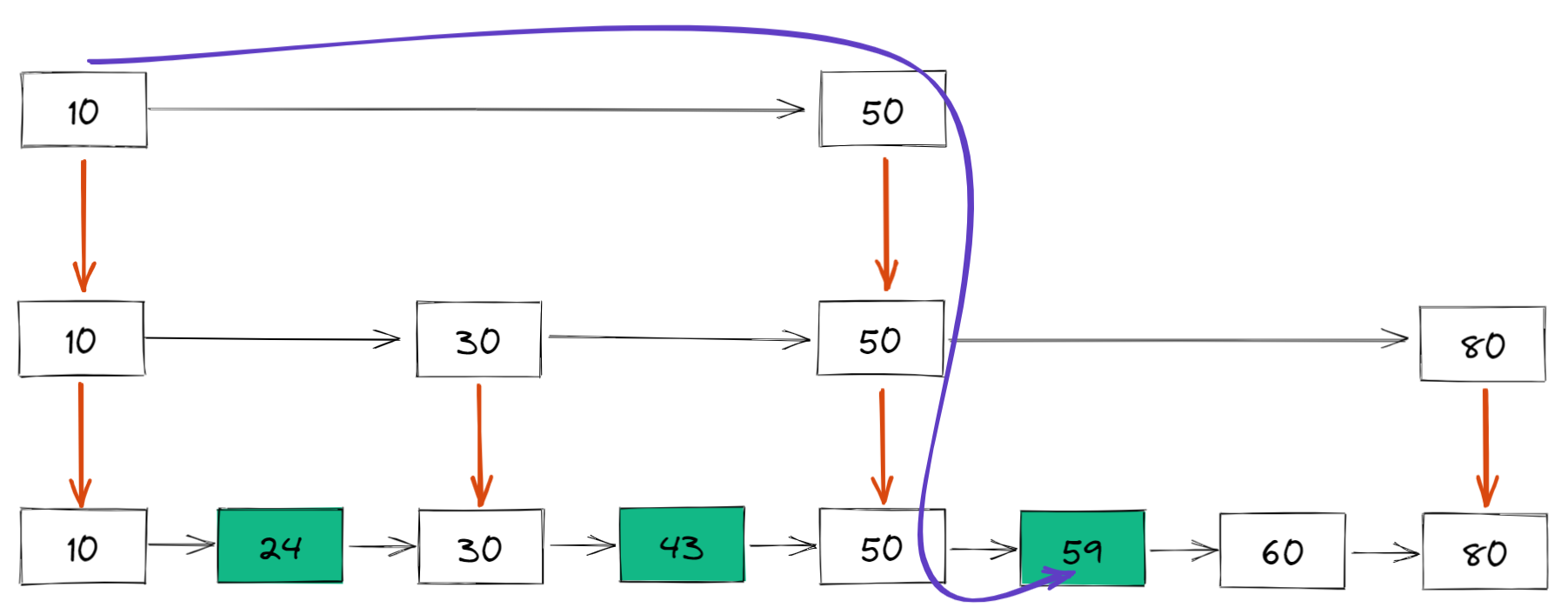
回顾下链表的定义:
class ListNode {
private int val;
private ListNode next;
public ListNode(int val) {
this.val = val;
this.next = null;
}
}
我们在每一个节点的基础上添加一个 down 指针,用来指向下一层的节点
class Node {
private int val;
private ListNode next;
private ListNode down;
public ListNode(int val) {
this.val = val;
this.next = null;
this.down = null;
}
}
这样,一个最简单的跳表节点就定义出来了。
我们这里说的只是最简单的实现,像比如 Redis 的跳表实现和我们说的还是有所不同的,当然了,思想都是一致的
所以跳表是什么?简单来说,跳表就是支持二分查找的有序链表
具体的搜索算法如下:
/* 如果存在 x, 返回 x 所在的节点, 否则返回 x 的后继节点 */
private Node find(x) {
p = top;
while (true) {
while (p.next.val < x){
p = p.next;
}
if (p.down == null){
return p.next;
}
p = p.down;
}
return null;
}
插入
关于插入,大家可能很容易想到往最下面一层的有序链表中添加数据,但是索引该咋办?索引要不要更新呢?
如果不更新索引,就可能出现两个索引节点之间数据非常多的情况,极端情况下跳表就会退化为单链表,从而使得查找效率从 O(LogN) 退化为 O(N)。
所以,我们在插入数据的时候,索引节点也需要相应的改变来避免查找效率的退化
比较容易想到的做法就是完全重建索引,我们每次插入数据后,都把这个跳表的索引删掉全部重建。因为索引的空间复杂度是 O(N),即:索引节点的个数是 O(N) 级别,每次完全重新建一个 O(N) 级别的索引,时间复杂度也是 O(N) 。造成的后果是:为了维护索引,导致每次插入数据的时间复杂度变成了 O(N)。
那有没有其他效率比较高的方式来维护索引呢?
最理想的索引就是在原始链表中每隔一个元素抽取一个元素做为一级索引。换种说法,我们在原始链表中【随机】的选 n/2 个元素做为一级索引是不是也能通过索引提高查找的效率呢?
当然可以,因为一般随机选的元素相对来说都是比较均匀的。如下图所示,随机选择了 n/2 个元素做为一级索引,虽然不是每隔一个元素抽取一个,但是对于查找效率来讲,影响不大,比如我们想找元素 16,仍然可以通过一级索引,使得遍历路径较少了将近一半。

当然了,如果抽取的一级索引的元素恰好是前一半的元素 1、3、4、5、7、8,那么查找效率确实没有提升,但是这样的概率太小了。所以我们可以认为:当原始链表中元素数量足够大,且抽取足够随机的话,我们得到的索引是均匀的。所以,我们可以维护一个这样的索引:随机选 n/2 个元素做为一级索引、随机选 n/4 个元素做为二级索引、随机选 n/8 个元素做为三级索引,依次类推,一直到最顶层索引。这里每层索引的元素个数已经确定,且每层索引元素选取的足够随机,所以可以通过索引来提升跳表的查找效率。
那代码具体该如何实现,使得在每次新插入元素的时候,尽量让该元素有 1/2 的几率建立一级索引、1/4 的几率建立二级索引、1/8 的几率建立三级索引....呢?
其实很简单啦,搞一个概率算法就行了(具体是怎么个概率法这里就不详细解释了),当每次有数据要插入时,先通过概率算法告诉我们这个元素需要插入到几级索引中,然后开始维护索引并把数据插入到原始链表中。
如下所示,插入新元素 12,假设概率算法返回的结果是 4,表示新元素需要插入到 4 级索引中,同时,我们还需要建立 3 级索引、2 级索引和 1 级索引(也就是原始有序链表)
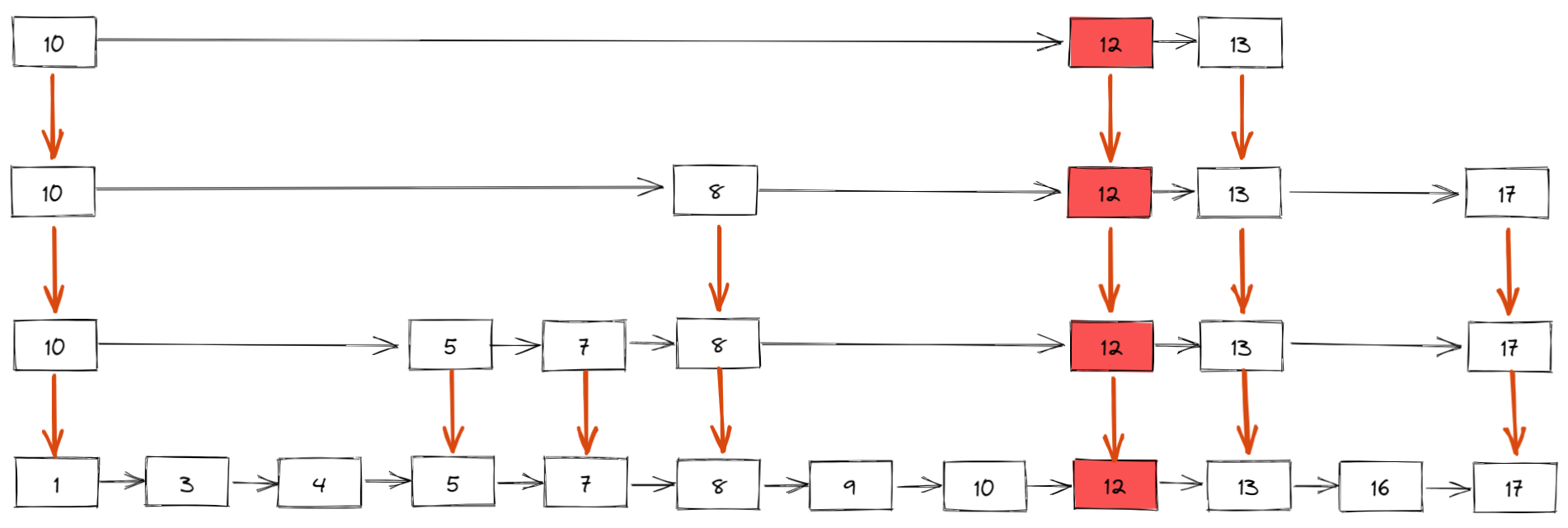
那插入数据时维护索引的时间复杂度是多少呢?
跳表中,每一层索引都是一个有序的单链表,元素插入到单链表的时间复杂度为 O(1),我们索引的高度最多为 LogN,当插入一个元素 x 时,最坏的情况就是元素 x 需要插入到每层索引中,所以插入数据的最坏时间复杂度是 O(LogN),最好的时间复杂度是 O(1)。
删除
跳表删除数据时,要把索引中对应节点也要删掉。如下图所示,如果要删除元素 8,需要把原始链表中的 8 和第 2、3 级索引的 8 都删除掉。
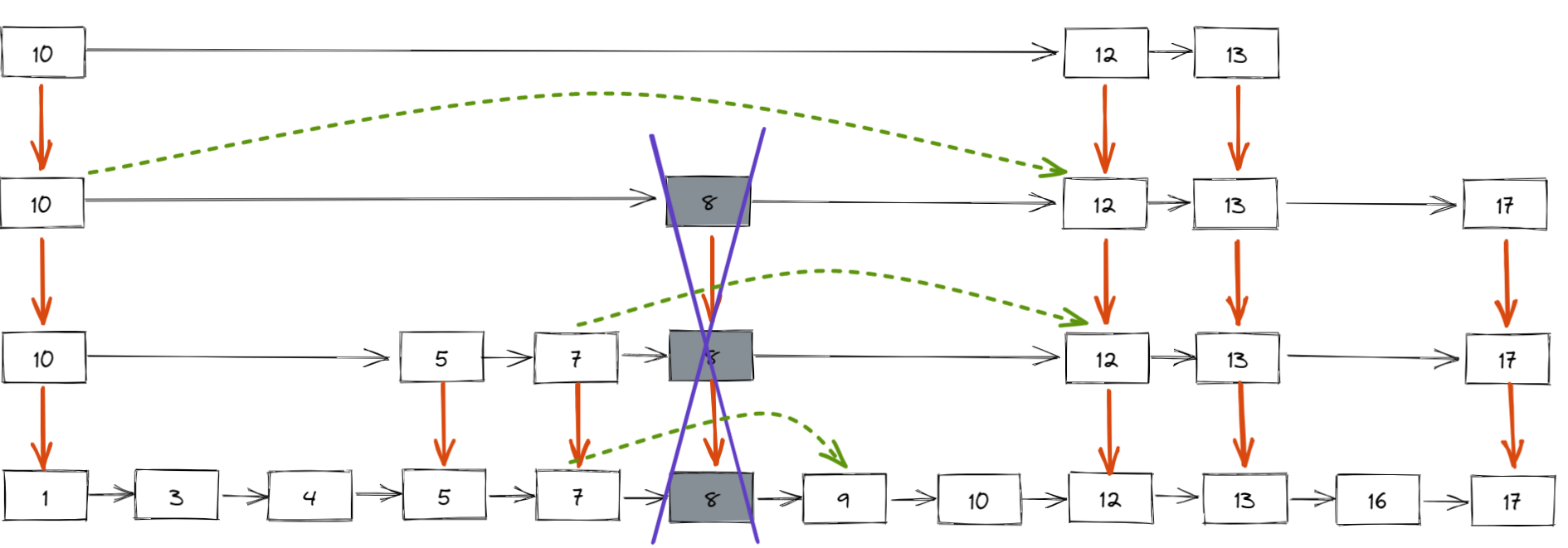
删除元素的过程跟查找元素的过程类似,只不过在查找的路径上如果发现了要删除的元素 x,则执行删除操作。
跳表中,每一层索引都是一个有序的单链表,单链表删除元素的时间复杂度为 O(1),最多需要删除 LogN 个元素(索引层数为 LogN),所以删除元素的总时间包 = 查找元素的时间 + 删除 LogN 个元素的时间 = O(LogN ) + O(LogN ) = 2O(LogN ),忽略常数部分,删除元素的时间复杂度为 O(LogN)。