kruskalCase克鲁斯卡尔算法

news2025/1/11 5:10:25

介绍

它的特点和Prim算法不一样，Prim是以点为主，通过顶点遍历没有访问的节点计算最小权重直至一条最小边出来；而Kruskal算法是以边为主，时间复杂度要低一些0(edge);

什么是最小生成树

最小生成树：在一个有n个结点的无向图中选出最少的边，保证所选边权相加之和最小以及该图中依然有n个结点并且n个结点连通。
一共有n个结点，要保证连通，至少需要n-1条边。
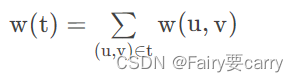
最小生成树的权值： $w ( t ) = ∑ ( u , v ) ∈ t w ( u , v ) w(t)=\sum\limits_{(u,v)\in t}^{}w(u,v)w(t)= (u,v)∈t∑w(u,v)$
下面我们用图看一下什么是最小生成树：

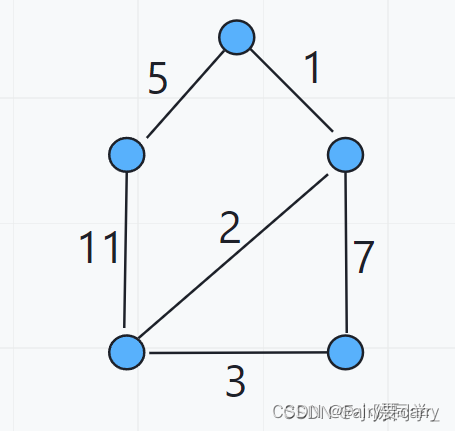
请添加图片描述
在该图中，我们留下这四条边就可以保证各个结点是连通的了，同时也保证所有边权之和最小，所以这个图的最小生成树权值为：1 + 2 + 3 + 5 = 11 1+2+3+5=111+2+3+5=11

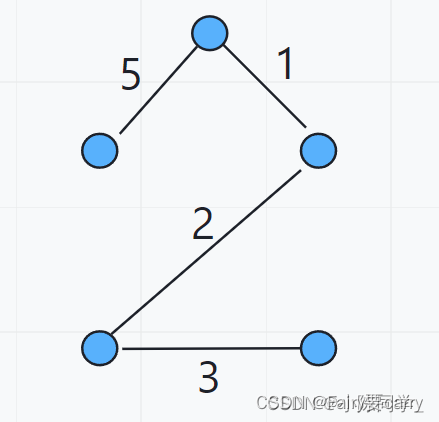
Kruskal思路：

首先按照边权从小到大排序
然后从小到大看每条边，判断两个节点的顶点是否是同一个，需要判断是否会回路

例子：
3. 开始克鲁斯卡尔算法来找到第一条边
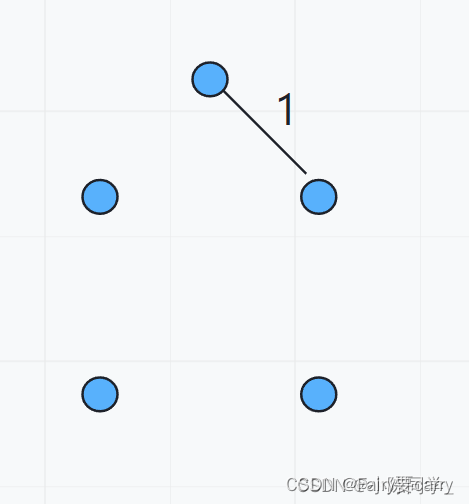
请添加图片描述
4. 找到第二条边

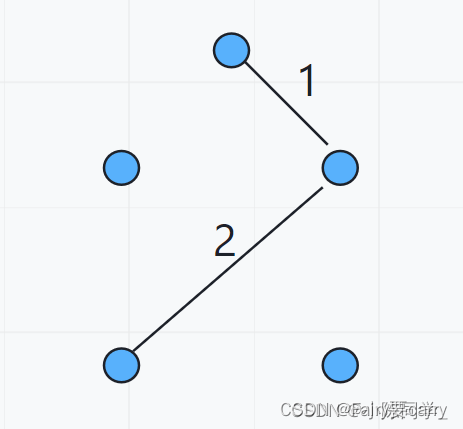
找到第三条边

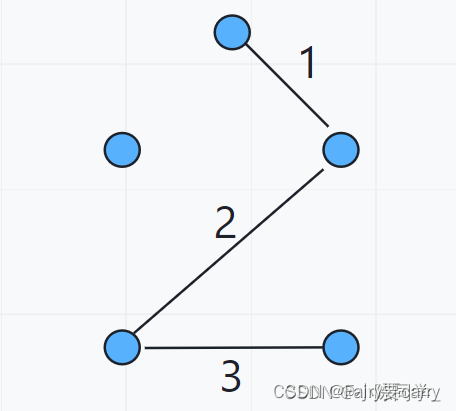
请添加图片描述
6. 最关键的第四条边
当你找到第四条边的时候会发现第四条边的两边所依附的节点已经是连通的了，根据克鲁斯卡尔算法需要将构成回路的边给去掉，因为你要计算最小生成树，既然这两个点已经连通了，那我们肯定是可以不选这条边的，不选这条边必然不会让结果变得更差，所以我们直接跳过这条边
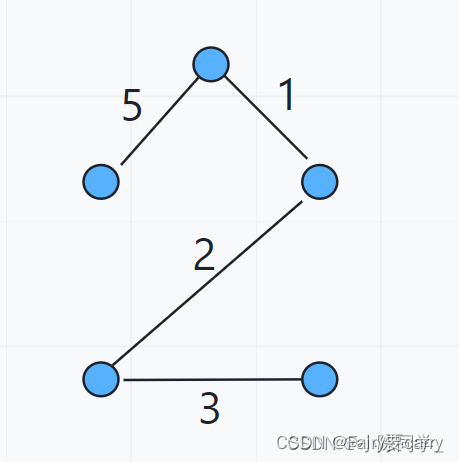
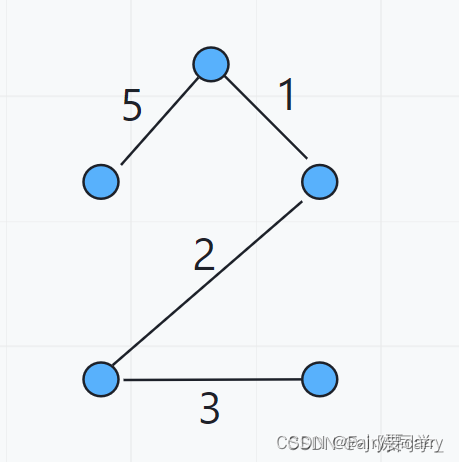
请添加图片描述
7. 计算第五条边
找到第五条边，找完五条边可以发现此时此刻所有的点已经连通了，最小生成树已经找到！
最小生成树的权值：1 + 2 + 3 + 5 = 11

代码实现

在这里插入图片描述

1.构造方法
在构造的时候我们会进行遍历矩阵判断节点是否有INF，如果都是有自己值的话就进行判断edgeNum++

 //1.构造克鲁斯卡尔的构造
    public KruskalCase(char[] vertexs, int[][] matrix) {
        /**
         * 1.初始化顶点数和边的个数
         */
        int vlen = vertexs.length;

        /**
         * 2.利用复制拷贝将传入的数组拷贝一份
         */
        this.vertexs = new char[vlen];
        for (int i = 0; i < vertexs.length; i++) {
            this.vertexs[i] = vertexs[i];
        }

        /**
         * 3.初始化边，使用的也是复制拷贝
         */
        this.matrix = new int[vlen][vlen];
        for (int i = 0; i < vlen; i++) {
            for (int j = 0; j < vlen; j++) {
                this.matrix[i][j] = matrix[i][j];
            }
        }

        /**
         * 4.统计边的条数
         */
        for (int i = 0; i < vlen; i++) {
            for (int j = i + 1; j < vlen; j++) {
                //4.1判断边是否有效（用INF来判断）
                if (this.matrix[i][j] != INF) edgeNum++;
            }
        }

    }

public static void main(String[] args) {
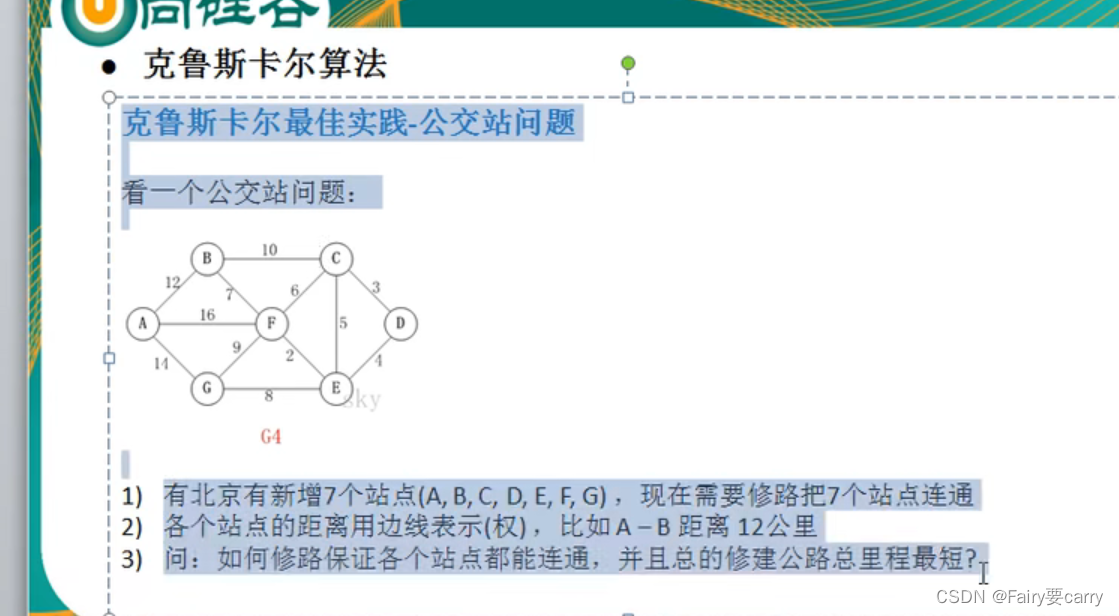
        char[] vertexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        int[][] matrix = {
                {0, 12, INF, INF, INF, 16, 14},
                {12, 0, 10, INF, INF, 7, INF},
                {INF, 10, 0, 3, 5, 6, INF},
                {INF, INF, 3, 0, 4, INF, INF},
                {INF, INF, 5, 4, 0, 2, 8},
                {16, 7, 6, INF, 2, 0, 9},
                {14, INF, INF, INF, 8, 9, 0}
        };
        KruskalCase kruskalCase = new KruskalCase(vertexs, matrix);
    }

2.将构造好的图打印出来

//2.打印邻接矩阵
    public void print() {
        System.out.println("邻接矩阵： \n");
        for (int i = 0; i < vertexs.length; i++) {
            for (int j = 0; j < vertexs.length; j++) {
                System.out.printf("%12d\t", matrix[i][j]);
            }
            System.out.println();
        }
    }

3.关键：将构造好的边进行排序处理

/**
     * 3.对边进行排序处理（冒泡排序）
     *
     * @param edges：边的集合
     */
    private void sortEdges(EData[] edges) {
        for (int i = 0; i < edges.length - 1; i++) {
            for (int j = 0; j < edges.length - 1 - i; j++) {
                if (edges[j].weight > edges[j + 1].weight) {
                    //进行交换
                    EData tmp = edges[j];
                    edges[j] = edges[j + 1];
                    edges[j + 1] = tmp;
                }
            }
        }
    }

4.寻找目标节点ch在数据数组中的下标位置

/**
     * 4.寻找对应的值的下标位置
     *
     * @param ch 顶点的值，比如'A','B'
     * @return 返回ch顶点对应的下标，如果找不到就返回-1
     */
    private int getPosition(char ch) {
        for (int i = 0; i < vertexs.length; i++) {
            if (vertexs[i] == ch) {
                return i;
            }
        }
        return -1;
    }

5.获取所有的边

/**
     * 5.获取图钟的边，将其放到EData[]数组当中
     * 通过邻接矩阵matrix获取
     *
     * @return
     */
    private EData[] getEdges() {
        int index = 0;
        //1.存储有效边的数组
        EData[] edges = new EData[edgeNum];
        for (int i = 0; i < vertexs.length; i++) {
            for (int j = i + 1; j < vertexs.length; j++) {
                //2.判断是否是有效边
                if (matrix[i][j] != INF) {
                    edges[index++] = new EData(vertexs[i], vertexs[j], matrix[i][j]);
                }
            }
        }
        return edges;
    }

在这里插入图片描述

7.获取下标i的顶点的终点——>在后面判断是否回路起到关键作用
思路：从ends数组中得到i的终点，并赋值给i返回的值为终点（一个变量i即可，减少了内存的消耗）

 /**
     * 6.功能：获取下标为 i 的顶点的终点，用于后面判断两个顶点的终点是否相同
     * 在已经生成边的时候才会进入while中，否则就是0
     * @param ends：记录了各个顶点对应的终点是哪个，ends是在遍历过程中，逐步形成的
     * @param i：表示传入顶点对应的下标
     * @return：返回的是下标为i的这个顶点对应的终点的下标
     */
    public int getEnd(int[] ends, int i) {
        //如果为0说明终点就是自己，ends装的是对应顶点i的终点
        while (ends[i] != 0) {
            i = ends[i];
        }
        return i;
    }

8.Kruskal算法的使用
1.首先得到所有的边
2.然后进行排序
3.遍历所有的边，判断是否构成回路，如果没有就加入到结果集中
得到中每条边的起点p1和终点p2，获取两个点的顶点判断是否构成回路，如果没有的话就将p1的终点的终点设置为p2的终点，并加入到结果集中

public void kruskal() {
        int index = 0; //表示最后结果的索引
        int[] ends = new int[edgeNum]; //用于保存“已有最小生成树中的每个顶点在最小生成树的终点"

        EData[] rets=new EData[edgeNum]; //保留结果，最后的最小生成树

        //1.获取图中所有边的集合，一共12条边
        EData[] edges = getEdges();
        System.out.println("图的边的集合=" + Arrays.toString(edges) + "共" + edges.length);

        //2.按照边的权值进行从小到大的排序
        sortEdges(edges);

        //3.遍历edges数组，将边添加到最小生成树时，判断准备加入的边是否会构成回路，如果没有就加入rets，否则不能加入
        for (int i = 0; i < edgeNum; i++) {
            //获取第i条边的第一个顶点（起点）
            int p1 = getPosition(edges[i].start);
            //获取到第i条边第2个顶点
            int p2 = getPosition(edges[i].end);

            //获取p1顶点在最小生成树的终点和 p2的顶点
            int m = getEnd(ends, p1);
            int n = getEnd(ends, p2);

            //4.判断是否构成回路
            if (m != n) { //终点不一致不构成回路——>m的顶点设置为n，也就是p1的顶点的顶点变为p2的顶点
                ends[m] = n; //设置m在已有最小生成树中的终点<E,F>[0，0，0，0，0，0，0，0，0，0，0]
                rets[index++]=edges[i];//有一条边加入到rets数组
            }

        }
        //5.输出最小生成树
        System.out.println("最小生成树为：");
        for (int i = 0; i < index; i++) {
            System.out.println(rets[i]);
        }
    }