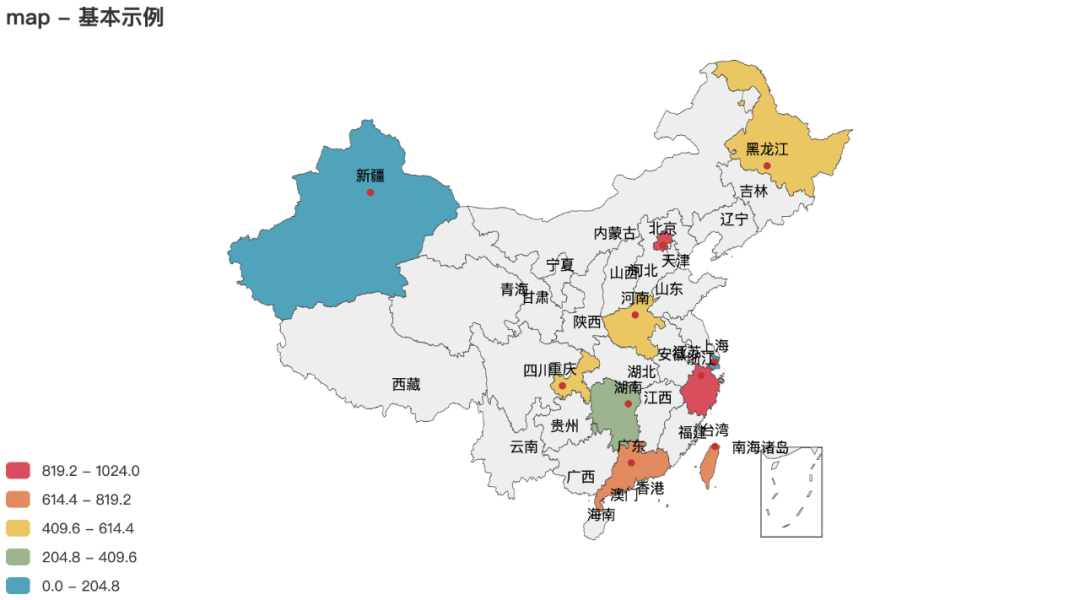
目录
- 测量
- 矩阵表示
- 中心化测度
- 度(degree)
- 路径(path)
- 特征向量中心
- 三元闭包和聚类系数
- 单纯同调
- 高阶Lapalacian算子
- 超图拉普拉斯
- 组合拉普拉斯
接上回说到了高阶的表示方法,接下来开始高阶系统的测量方法。
测量
具体来说就是可用于表征和量化高级系统每一个层次的结构特性的可观察性测量。
矩阵表示
In mathematics, the incidence matrix is the classical way to describe the relationships between two classes of objects.
图 G = ( V , E ) G = (V, E) G=(V,E) 的关联矩阵是 n × m n \times m n×m 矩阵 I = { I i α } I = \{I_{i \alpha}\} I={Iiα}:
- n n n 是节点数, m m m 是边的数量;
-
I
i
α
=
1
⟷
I_{i \alpha} = 1 \longleftrightarrow
Iiα=1⟷ 节点
i
i
i 和边
α
\alpha
α 相关联;否则为 0。
将该定义也可拓展到超图,如下图[A]。
同样的,由于图中邻接矩阵和关联矩阵具有关系: A = I I T − D . A = I I^{\text{T}} - D. A=IIT−D.

中心化测度
网络中心性是节点相关的度量,量化一个节点在网络中的“中心”程度。
度(degree)
根据邻接矩阵可定义度为:
deg
(
i
)
=
∑
j
=
1
n
a
i
j
.
{\text{deg}}(i) = \sum_{j = 1}^{n} a_{i j}.
deg(i)=j=1∑naij.
进而,在高阶情形下定义广义的度为:
k
d
,
δ
(
α
)
=
∑
α
′
⊃
α
a
α
′
.
k_{d, \delta} (\alpha) = \sum_{\alpha^{\prime} \supset \alpha} a_{\alpha^{\prime}}.
kd,δ(α)=α′⊃α∑aα′.
此处的
α
\alpha
α 指代
δ
<
d
\delta < d
δ<d 维的单纯形。但对于加权图,权重影响,处理方式又稍显复杂,具体可参见1。
路径(path)
顶点
v
i
v_i
vi的子类型图中心性是网络中从顶点
v
i
v_i
vi开始和结束的不同长度的闭合游动的数量,可以表示为:
C
s
h
=
∑
v
j
u
i
j
e
λ
j
,
C_{sh} = \sum_{v_{j}} u_{i j} e_{\lambda_{j}},
Csh=vj∑uijeλj, 其中,
u
i
j
u_{i j}
uij是邻接矩阵的第
j
j
j个特征向量的第
i
i
i个分量。

特征向量中心
单个节点特征向量的中心性取决于其邻居的中心性,量化了节点对网络的影响,而非可能路径的影响。其被定义为: χ v = 1 λ ∑ t ∼ v χ t = 1 λ ∑ t ∈ G a v t χ t . \chi_{v} = \frac{1}{\lambda} \sum_{t \sim v} \chi_{t} = \frac{1}{\lambda} \sum_{t \in G} a_{v t} \chi_{t}. χv=λ1t∼v∑χt=λ1t∈G∑avtχt.
三元闭包和聚类系数
- 网络分析中超越节点相关度量的一个关键概念是三元闭包。社会学认为,只有当两个人是三角形的一部分时,他们之间才会产生强烈的社会联系2。在图结构中,三元闭包表示为由第三条边闭合的长度为 2 2 2的路径。聚类系数是一个重要的网络度量,它决定了节点邻域的密度。该系数也可以全局计算为边缘闭合的路径的总百分比,即三角形的一部分。
将上述定义延拓至高维的思路有二:
- 通过增加局部聚类的定义,重新定义聚类系数;
- 或者重新定义高维walk,来保证三元闭包的路径特性。
单纯同调
由于是个代数渣渣,所有此处略。
高阶Lapalacian算子
超图拉普拉斯
区别主要在最后一项:
L
=
D
−
A
+
ρ
(
K
+
(
s
−
1
)
I
)
.
L = D - A + \rho(K + (s - 1)I).
L=D−A+ρ(K+(s−1)I).
其中,
ρ
=
d
/
N
\rho = d/N
ρ=d/N即平均度除以节点数;
K
K
K是完全图矩阵。
组合拉普拉斯

K. Kapoor, D. Sharma, J. Srivastava, Weighted node degree centrality for hypergraphs, in: 2013 IEEE 2nd Network Science Workshop (NSW), IEEE, 2013, pp. 152–155. ↩︎
M.S. Granovetter, The strength of weak ties, in: Social Networks, Elsevier, 1977, pp. 347–367. ↩︎