文章目录
- 参考
- 前言
- 拉格朗日函数
- 例1
- 例2
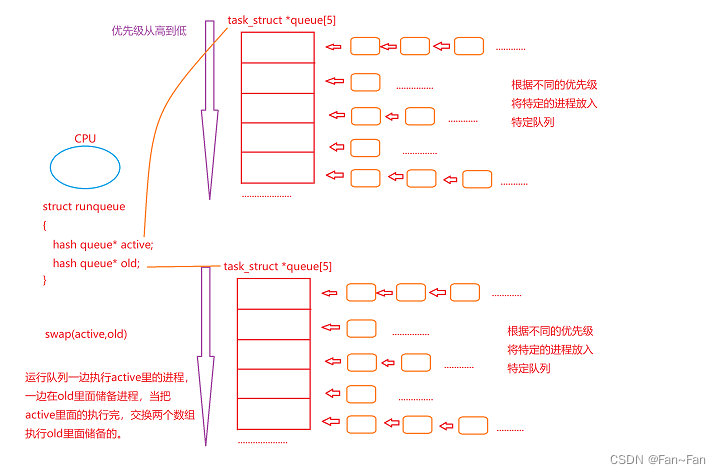
- 拉格朗日函数的对偶问题
参考
“拉格朗日对偶问题”如何直观理解?“KKT条件” “Slater条件” “凸优化”打包理解
感觉有时间看视频的还是看视频比较好,本文只是记录一下以防以后忘记。
前言
还记得SVM里用到拉格朗日对偶,将有约束条件转换成无约束条件问题进行最优值求解,其实也只是会用这个方法而已,至于为啥能这么用,还是不知道的,接下来深入理解一下吧,也为了之后学习正则化做铺垫。
拉格朗日函数

其中f0(x)是我们的目标函数。
fi(x)则是需要考虑的约束条件。
那么根据这种转换我们可以看一下几个简答的例子:
例1

可以看出在相切的点就是极值了,因为梯度是个向量,只有目标函数的梯度和约束条件的梯度方向一致,相加才可能为0,才能够满足约束条件的情况下取到极值,梯度方向一致可以通过调整λ大小来使得二者梯度能够大小相等,方向相反,相加就为0了。
例2

假设现在有5个约束条件,分别在图中画出。
可以看到生成与目标函数相反方向的梯度,只有两个约束条件的梯度能做出这样的贡献

他们那个点的梯度和是目标函数的相反的梯度。
对于没有用到的约束条件,则他们的梯度应当为0,如果不为0就不会满足约束条件和目标函数梯度的和为0这个条件了。

从下图中我们可以看出,箭头的方向都是直线上的点对应得梯度的方向
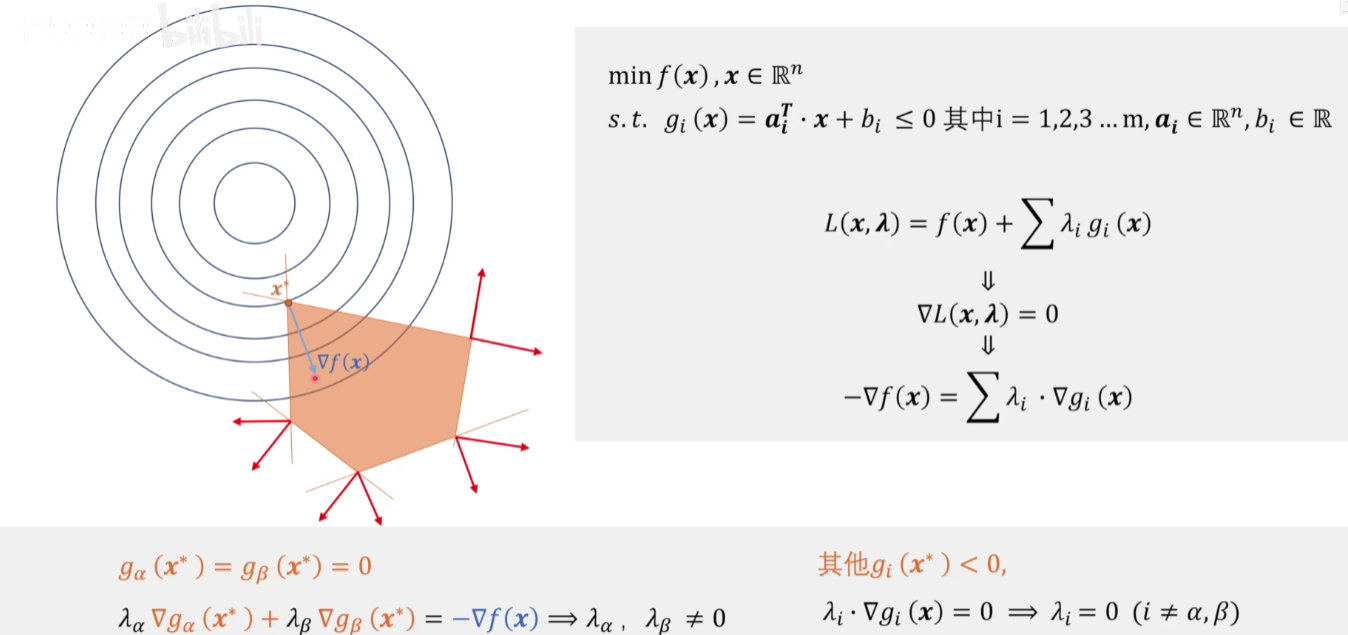
如果λ允许取负数,那么其实别的约束条件梯度的组合也可能满足与目标函数的大小相同,方向相反,因此我们需要规定λ>=0.

松弛说明约束条件并没有起到约束的作用,缺少了结果也不会受到影响。
紧致说明约束条件起导论约束的作用,如果缺少这个条件,结果会发生改变。
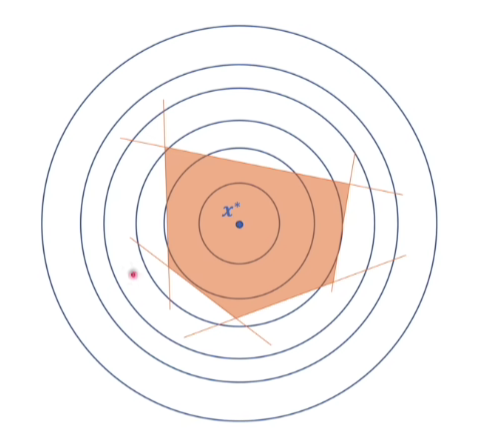
例如这种情况下,对于求最小值来说,所有约束条件都是松弛的。
拉格朗日函数的对偶问题
首先给出一个等价的问题表达:

因为λ和μ是可以任意取的,因此当不满足约束条件的时候,L(x,,λ,μ )都是能取到无穷大的,不过外面还有个取最小值,因此不符合约束条件的都会被舍弃,那么剩下的就是符合约束条件的,最后的结果也就是需要求的最小值了。
如果将上面的问题看作原问题那么对偶问题就如下:

需要引入一个对偶函数,相当于将计算最大最小的顺序反一下。
对偶问题还能够等价写成:

假设我们已经找到了解,对偶函数的特征如下:

变量都是一阶线性的关系,因为线性函数一定是个凸函数或者凹函数,因为这里是要求对偶函数的最大值,我们就能将他看成一个凹函数了。(凹函数加个-号就是凸函数了)
因此,不论原问题的约束条件目标函数是什么,当其能转换为对偶问题时,那么他一定是个凸优化问题。求解就比较方便了。
虽然转换成对偶问题容易,但是对偶问题的解和原问题的解相等,是需要条件的。

通过推导可知,原问题的解一定是>=对偶问题的解的。
当满足Slater条件,说明原问题和对偶问题有强对偶性。
但是在机器学习SVM中我们经常遇到的KKT条件

一般来说,大多数问题对偶问题满足KKT条件应该就是原问题的强对偶问题了,但是理论上KKT条件只是一个必要条件,就是说如果满足强对偶问题,那么一定满足KKT条件,但是反过来就不一定了,但是由于大多数情况下反过来也是,那么就这么用问题也不大。