0、概括

• Manacher算法用于求解字符串中最长回文子串问题。

• Manacher算法的核心：

  1. 理解回文半径数组；
  2. 理解所有中心的回文最右边界 R，和取得 R 时的中心点 C；
  3. 理解 L...(i')...C...(i)...R 的结构，以及根据 $i^{\prime }$ 回文长度进行的状况划分
  4. 每一种情况划分，都可以加速求解 $i$ 回文半径的过程

• 补充：子串一定是连续的，如 abc123321def，最长回文子串就是 123321。

• 实际可用于DNA序列的研究。

1、引入

假设字符串 str 长度为 $N$，想返回最长回文子串的长度，且要求时间复杂度为 $O(N)$。

2、暴力解找最长回文子串

【方法一】

直接以每个位置的字符作为中心点往两侧扩，比较左右两侧的字符是否相等，如果相等继续比较两侧的下一个字符，但是这种方法对于偶数长度的回文子串不适用。

【方法二】

那怎么办呢？处理原始字符串：最左边添加一个 #，每两个字符之间都添加一个 #，最后一个字符后也添加#。

如原始字符串为 121aaaa232aa，处理后的字符串变为 #1#2#1#a#a#a#a#2#3#2#a#a#。

好处：将处理后的字符串的每个字符位置作为中心往两侧扩，得到的最大长度除以 2，就能得到原始串的一个回文长度。

问：如果将原始串处理成新串的时候不用字符 #，而是用一个原始串中已经出现过的字符，会不会形成干扰？

答：不会，因为以任何位置为中心往两边扩的时候，都是实际的字符在比较，新加的字符在比较，不会存在实际字符和新加字符比较的情况，所以这个新加的字符是什么都可以。

时间复杂度：以 aaaaa 字符串为例，处理后的字符串 #a#a#a#a#a#，以每个位置为中心往两边扩需要比较的次数依次为：0 + 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 + 0，以字符串的中间位置为轴，左右两边都是等差数列，所以总的时间复杂度是 $O(n^2)$。

之所以暴力解的过程慢，是因为以每个位置为中心往两侧扩的操作都是独立的，也就是之前的操作对于之后的操作没有任何指导意义。

3、Manacher算法找最长回文子串

Manacher算法在一个长度为 $N$ 的字符串中找到最长回文子串的时间复杂度为 $O(N)$。

基础概念

• 回文直径 和 回文半径

abc12321def：回文串为“12321”，回文直径为5，回文半径为3

1221: 回文串为“1221”，回文直径为4，回文半径为2

• 回文半径数组

记录从左往右以每个位置为中心向左右两边扩的长度

• 最右回文边界

整型变量，用 R 表示，初始时R = -1。

图解R：


不管是以哪个位置为中心扩的，只要让这个回文区域的右边界变得更右了，R就记录这个更往右的位置。

• 最右回文边界的中心

用 $C$ 变量表示，记录是哪个中心点使得R往右扩的。如上图解中，C依次为0、1、2、3、5，R不更新C就不会更新，R一旦更新，C一定会跟着更新。

流程

以 $i$ 位置为中心向左右两边扩，可能会遇到的情况：

1. $i$ 没有被 $R$ 罩住（$i$ > $R$），则不优化，直接暴力扩；
2. $i$ 被 $R$ 罩住（$i<=R$)，可以优化。这时候 $C$ 在 $i$ 左边， $R$ 在 $i$ 右边，以 $C$ 为中心点，一定能找到 $i^{\prime }$，以及$R$ 的对称点 $L$，如果 $i$ 被 $R$ 罩住一定存在这种拓扑关系：
   
   然后根据 $i^{\prime }$ 能扩多大的区域的信息来分类：
   • case1 : $i^{\prime }$ 扩出的区域在 $(L,R)$内
     
     
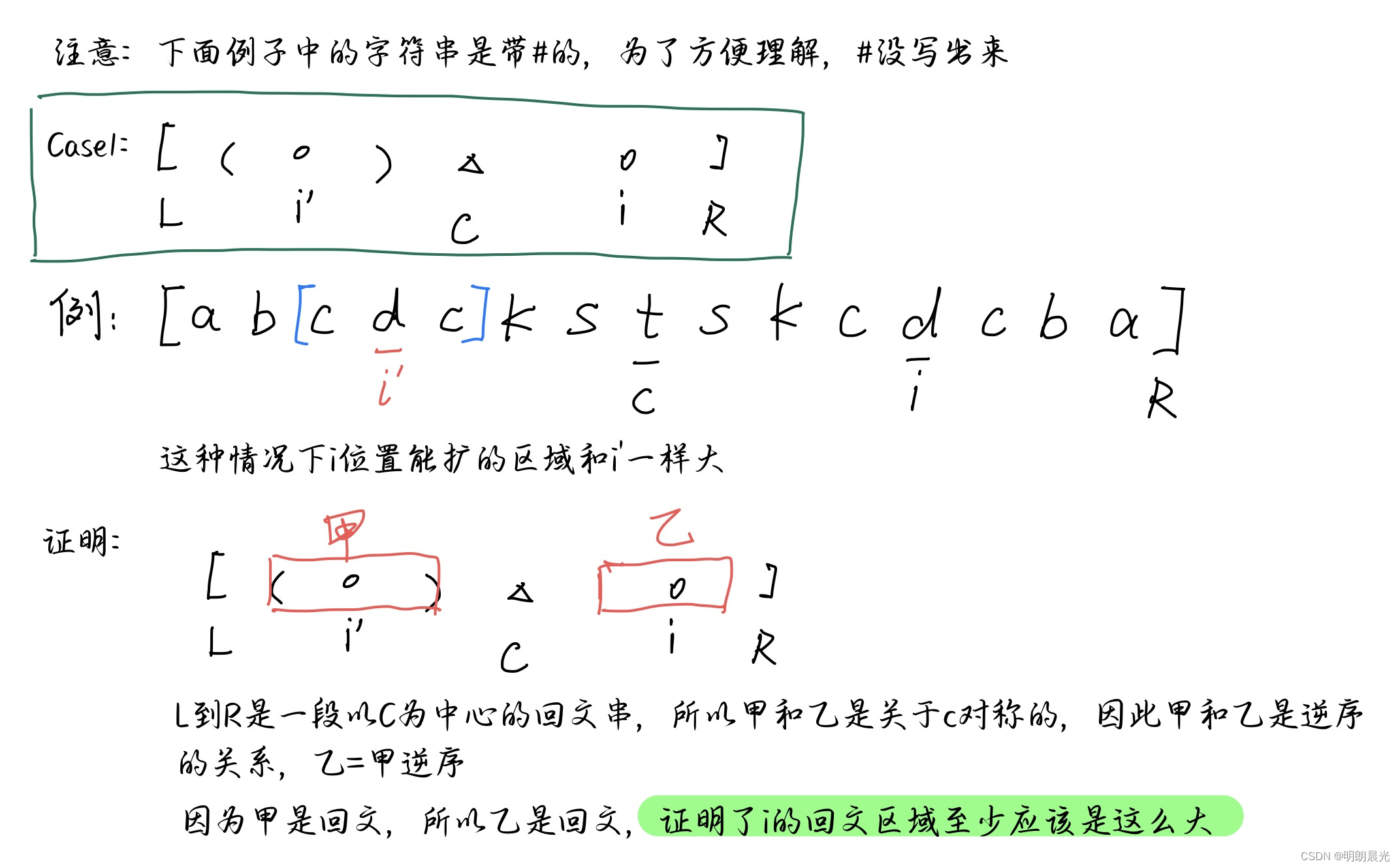
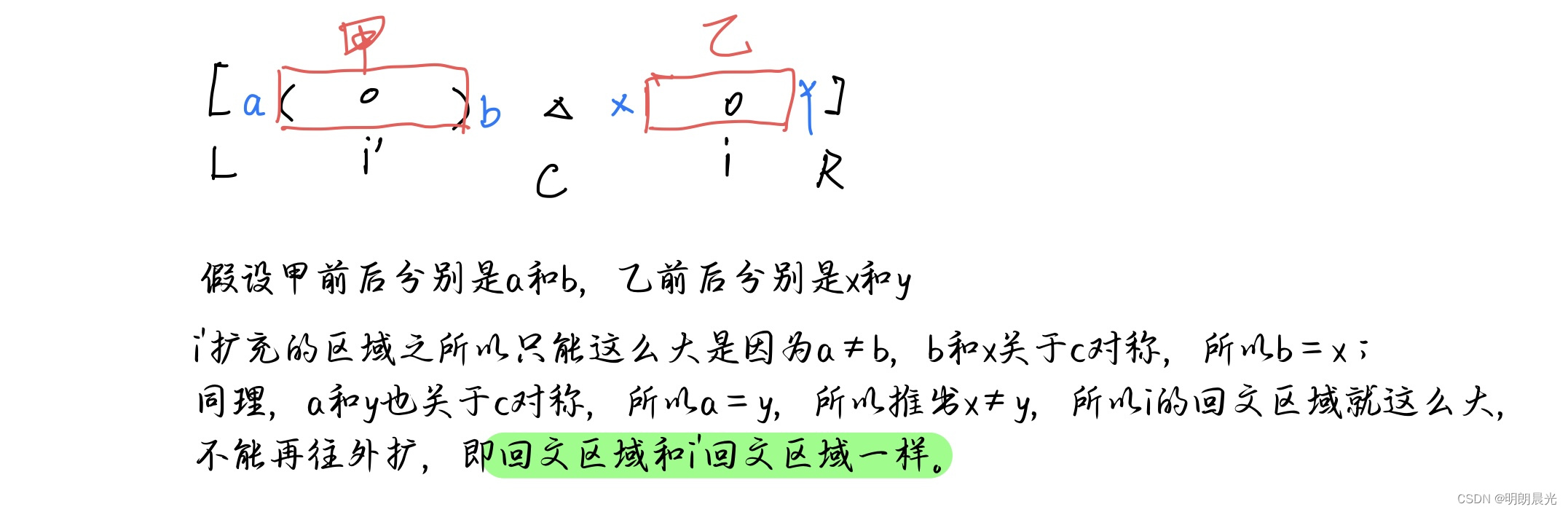
   • case 2：$i^{\prime }$的回文区域在 $[L,R]$ 之外
     
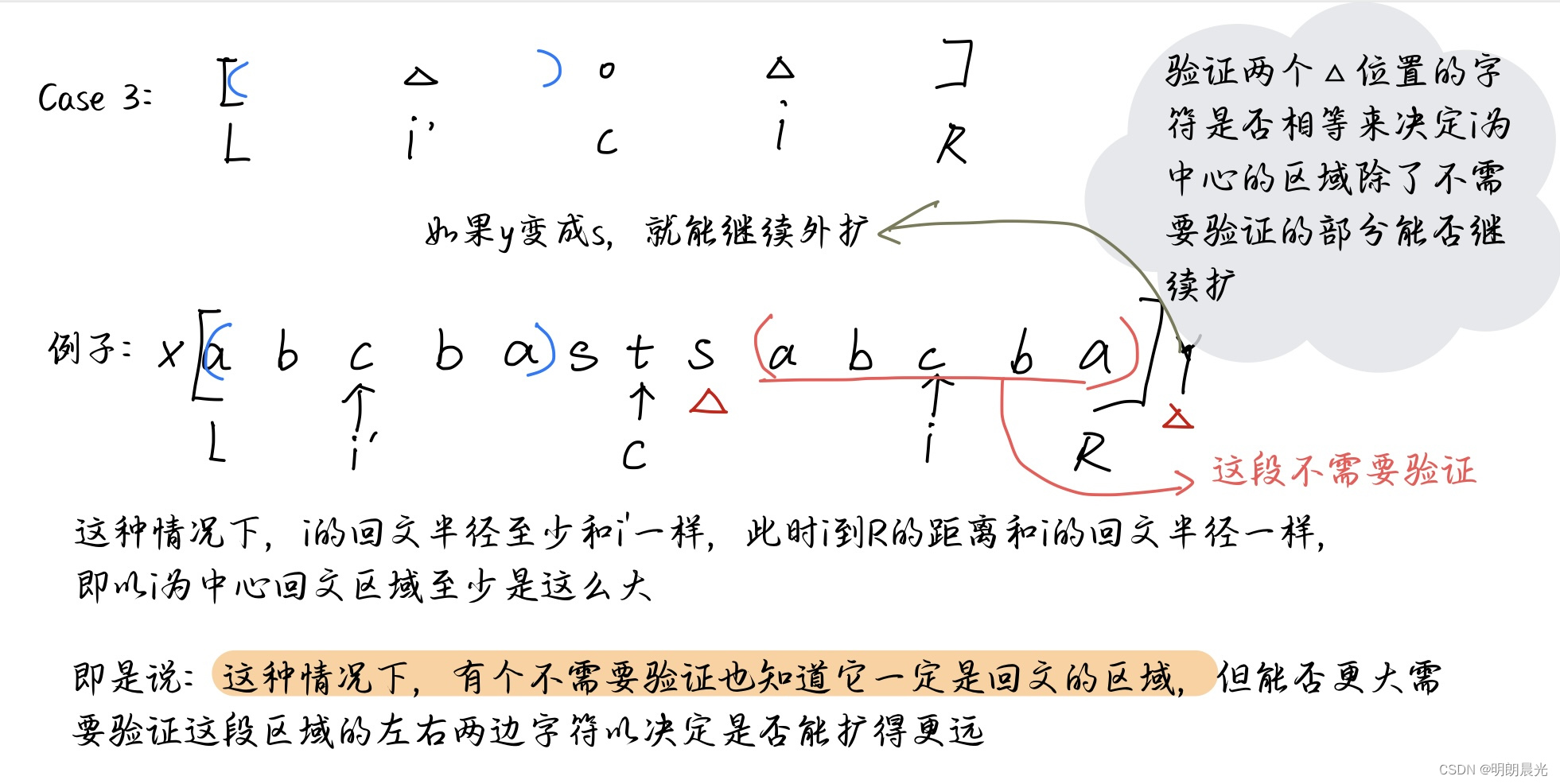
   • case3：$i^{\prime }$为中心的的回文区域左边界和 $L$ 压线

整理各种情况，可得伪代码：

1）i > R, 无优化，暴力扩
2）i <= R:
	① i’扩充的区域在(L, R) 内，直接得到答案和i'的回文区域一样，不用扩，O(1)
	② i'扩充的区域左边界 < L，右边界 < R, 即不完全在(L,R)范围内，也不用扩，回文半径为 i 到 R 的距离，也是直接得到答案，O(1)
	③ i'扩充的区域左边界 = L，右边界 < R, i 到 R 这段为半径的区域不需要验证，再往右的位置对应左边继续往下验

复杂度分析：任何一个位置，都可能会失败一次（遇到不匹配的或没有字符了），失败的总次数 $N$ 次；如果匹配成功，一定会使得 $R$ 变大，2) 的 ①② 本来就是 $O(1)$ 复杂度，不需要再讨论；而 2) 的 ③ 情况 $R$ 内部不验，$R$ 外部继续往右的时候，如果失败了就1次，如果成功依然会使得 $R$ 变大。而 $R$ 的变化有极限($0$~$N$)，且整个方法中，只要匹配成功，$R$ 就增大，$R$ 是不回退的，所以整个方法的时间复杂度$O(N)$。

4、Manacher算法代码实现

public class Manacher {
	//返回最长回文子串的长度
	public static int manacher(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		//1. 处理字符串，原始字符串处理为manacher字符串，即给前后和字符间的位置添加#
		//例："12132" -> "#1#2#1#3#2#"
		char[] str = manacherString(s); 
		
		// 回文半径数组，该数组中的最大值/2就是结果
		int[] pArr = new int[str.length];
		
		int C = -1;
		// 讲解时：R代表最右的扩成功的位置
		// coding：最右的扩成功位置的，再下一个位置，即失败的位置
		int R = -1;
		int max = Integer.MIN_VALUE;
		
		//2. 以每个位置为中心点进行往左右扩的操作
		for (int i = 0; i < str.length; i++) { // 0 1 2
			// R第一个违规的位置，i<R 时，i才在R（扩成功的区域，即讲解时的R）内部；而i>=R时，i在R（扩成功的区域，即讲解时的R）外部
			// 如果i在R外（i>=R) ，以i为中心的回文半径至少是1（它自己）；
			// 如果i在R内（i<R)，就要用之前讨论的三种情况细分（根据i’的扩的区域）：
			// 1）i’扩的区域在(L,R)内，i扩的区域 = i‘扩的区域
			// 2）i'扩的区域在[L,R]外，i扩的区域：i到R的距离为回文半径
			// 3）i'扩的区域左边界在L，i扩的区域：至少i到R的距离不用验
			// 下面这句代码就可以完成：
			// 2 * C - i 就是i'，R - i 是i到R的距离，意思就是i‘的回文半径长度和R到i的距离，谁小就是至少不用验的区域
			// 这句代码的结果就是哪个区域不用验，也就是i位置扩出来的答案，i位置扩的区域，至少是多大。
			pArr[i] = R > i ? Math.min(pArr[2 * C - i], R - i) : 1;
			
			//不用验的区域的左右两侧的字符进行比较，就是往外扩的过程
			//上述的三种情况中，不用验的两种情况1）和2）在第一次进入这个循环就会break
			while (i + pArr[i] < str.length && i - pArr[i] > -1) {
				if (str[i + pArr[i]] == str[i - pArr[i]])
					pArr[i]++;
				else {
					break;
				}
			}
			
			//更新R和C的值
			if (i + pArr[i] > R) {
				R = i + pArr[i];
				C = i;
			}
			//max最后记录的是最大回文半径，而且是处理后的字符串的回文半径
			//如121，处理后#1#2#1#，回文半径为4,4-1=3就是原字符串的最大回文串长度
			//偶回文同样1221，处理后#1#2#2#1#，回文半径为5,  5-1=4就是原字符串的最大回文长度
			max = Math.max(max, pArr[i]); 
		}
		return max - 1;
	}

	public static char[] manacherString(String str) {
		char[] charArr = str.toCharArray();
		char[] res = new char[str.length() * 2 + 1];
		int index = 0;
		for (int i = 0; i != res.length; i++) {
			res[i] = (i & 1) == 0 ? '#' : charArr[index++];
		}
		return res;
	}

	// for test
	public static int right(String s) {
		if (s == null || s.length() == 0) {
			return 0;
		}
		char[] str = manacherString(s);
		int max = 0;
		for (int i = 0; i < str.length; i++) {
			int L = i - 1;
			int R = i + 1;
			while (L >= 0 && R < str.length && str[L] == str[R]) {
				L--;
				R++;
			}
			max = Math.max(max, R - L - 1);
		}
		return max / 2;
	}

	// for test
	public static String getRandomString(int possibilities, int size) {
		char[] ans = new char[(int) (Math.random() * size) + 1];
		for (int i = 0; i < ans.length; i++) {
			ans[i] = (char) ((int) (Math.random() * possibilities) + 'a');
		}
		return String.valueOf(ans);
	}

	public static void main(String[] args) {
		int possibilities = 5;
		int strSize = 20;
		int testTimes = 5000000;
		System.out.println("test begin");
		for (int i = 0; i < testTimes; i++) {
			String str = getRandomString(possibilities, strSize);
			if (manacher(str) != right(str)) {
				System.out.println("Oops!");
			}
		}
		System.out.println("test finish");
	}
}