C-RNN-GAN: Continuous recurrent neural networks with adversarial training 2016

Abstract

生成对抗网络已被提出作为一种有效训练深度生成神经网络的方法。我们提出了一种生成对抗模型，它适用于连续的序列数据，并通过在古典音乐集合上训练它来应用它。我们得出的结论是，随着模型的训练，它生成的音乐听起来越来越好，报告生成的音乐的统计数据，并让读者通过下载生成的歌曲来判断质量。

1 Introduction

我们提出了一种循环神经网络架构C-RNN-GAN(连续RNN-GAN)，它经过对抗性训练来建模序列的整个联合概率，并能够生成数据序列。我们的系统通过在中等格式的古典音乐序列上进行训练来证明，并使用音阶一致性和音域等指标进行评估。

我们得出的结论是，生成式对抗训练是一种可行的训练网络的方式，它可以对连续数据序列上的分布进行建模，并看到了对许多其他类型的连续数据建模的潜力。

2 C-RNN-GAN: A continuous recurrent network with adversarial training

该模型是一种带有对抗训练的递归神经网络。对手是两个不同的深度循环神经模型，一个生成器(G)和一个鉴别器(D)。生成器被训练来生成与真实数据难以区分的数据，而鉴别器被训练来识别生成的数据。训练变成了一个零和游戏，其中纳什均衡是当生成器产生的数据鉴别器无法从真实数据中区分出来。我们定义如下损失函数LD和LG:

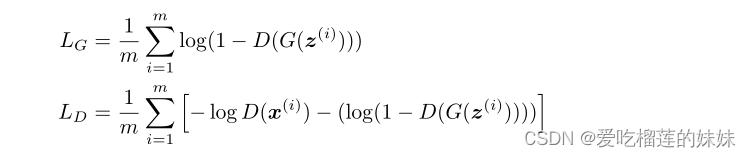
(其中z(i)是[0,1]k中的均匀随机向量序列，x(i)是来自训练数据的序列。K为随机序列中数据的维数。)G中每个单元格的输入是一个随机向量，与前一个单元格的输出相连接。

在训练rnn作为语言模型时，从前一个单元输入输出是常见的做法[Mikolov等人，2010]，也被用于音乐创作[Eck和Schmidhuber, 2002]。

鉴别器由一个双向循环网络组成，允许它在决策时考虑两个方向的上下文。在这项工作中，使用的循环网络是长短期记忆(LSTM) [Schmidhuber和Hochreiter, 1997]。它有一个带有门的内部结构，有助于解决梯度消失问题，并学习更长的依赖关系[Hochreiter, 1998, Bengio等人，1994]

 2.1 Modelling music 音乐建模

在这项工作中，我们开始评估使用生成对抗模型来学习古典音乐背后的生成分布的可行性。受数字乐器之间通信信号的古老MIDI格式的启发，我们在每个数据点上用四个实值标量对信号进行建模:音调长度、频率、强度和从前一个音调开始花费的时间。以这种方式对数据进行建模，使网络能够表示多音和弦(两个音调之间的时间为零)。为了评估它对复调的影响，我们还试验了在G中每个LSTM单元输出最多三个音调(对D进行相应的修改)。然后，每个音调用上面描述的自己的四组值表示。我们将此版本称为C-RNN-GAN-3。与MIDI格式类似，音色的缺失由零强度输出表示。

3 Experimental setup 实验设置

模型布局细节:G和D中的LSTM网络深度为2，每个LSTM单元有350个内部(隐藏)单元。D是双向布局，G是单向布局。D中每个LSTM单元的输出被馈电到具有跨时间步长的共享权重的全连接层，然后每个单元的一个sigmoid输出被平均到序列的最终决定。

基线:我们的基线是一个循环网络，类似于我们的生成器，但完全训练为在循环中的每个点预测下一个音调事件。

数据集:训练数据来自网络，以midi格式的音乐文件形式收集，包含著名的古典音乐作品。“note on”类型的每个midi事件连同其持续时间、音调、强度(速度)和从最后一个音调开始的时间一起被加载和保存。

音调数据在内部用相应的声音频率表示。在内部，所有数据都标准化为每个四分音符384个刻度分辨率。数据包含了来自160位不同古典音乐作曲家的3697个midi文件。

源代码可以在Github1上获得，包括一个实用程序，可以从不同的网站下载本研究中使用的所有数据。

训练:采用时间反向传播(BPTT)和小批量随机梯度下降法。学习率设置为0.1，我们对G和D中的权重应用L2正则化。

该模型预训练6个周期，误差损失为平方，用于预测训练序列中的下一个事件。与对抗性设置一样，每个LSTM单元的输入是一个随机向量v，与前一个时间步的输出相连接。V均匀分布在[0,1]k中，取k为每个音调的特征个数，4。在预训练期间，我们使用了一个序列长度的模式，从训练数据中随机采样的短序列开始，最终用越来越长的序列训练模型。我们认为这是课程学习的一种形式，我们从学习短文开始，学习时间相近的点之间的关系。

在对抗性训练中，我们注意到D会变得过于强大，导致无法用于改善g的梯度，这种影响在没有预训练的情况下初始化网络时尤为明显。为此，我们应用了冻结[Salimans et al.， 2016]，即当D的训练损失小于G的训练损失的70%时，停止D的更新。当G变得过于强大时，我们做相应的事情。

我们还采用特征匹配[Salimans等人，2016]，这是一种鼓励G中更大方差的方法，并通过替换标准发生器损耗LG来避免对电流鉴别器的过拟合。

通常，生成器的目标是使鉴别器的错误最大化，但对于特征匹配，目标是在鉴别器的某个级别上产生与真实数据匹配的内部表示。我们从D中最后的逻辑分类层之前的最后一层中选择表示R，并为G定义新的目标LG。

 

 

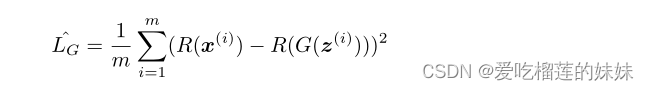
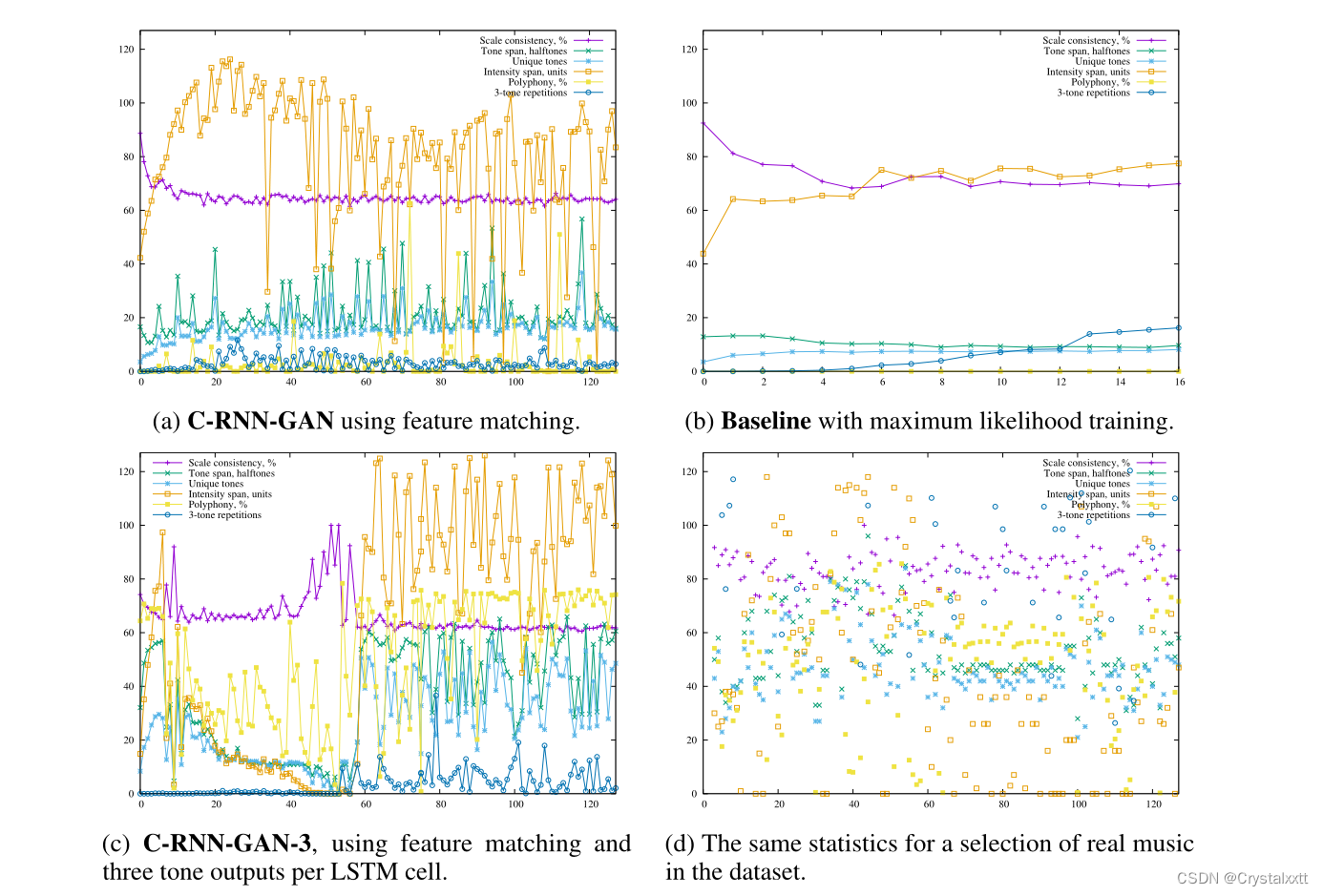
图3:评估模型生成的音乐的统计数据。C-RNN-GAN (a)在训练过程中生成越来越复杂的音乐。使用的独特音调的数量有模糊增加的趋势，而音阶一致性似乎在十或十五个周期后稳定下来。

三音重复在前25个周期有增加的趋势，然后保持在一个相当低的水平，似乎与使用的音调数有关。基线模型(b)没有达到相同的变化水平。使用的唯一音调的数量一直很低，而音阶一致性似乎与C-RNN-GAN相似。与C-RNN-GAN相比，音调跨度更接近于唯一音调的数量，这表明基线在使用的音调中具有较小的可变性。与c - rnn - gan和基线相比，c - rnn - gan -3 (c)获得了更高的复音得分。C-RNN-GAN-3在第50到55个纪元左右达到许多零值输出的状态后，在音调跨度、唯一音调的数量、强度跨度和3个音调重复上达到了更高的值。在(d)中，可以看到真实的音乐具有与生成音乐相似的强度跨度。量表一致性稍高，但也变化较大。复调评分与C-RNN-GAN-3相似。3音的重复要高得多，但由于歌曲的长度不同，很难进行比较。计数通过除以lr/lg进行标准化，其中lr是真实音乐的长度，lg是生成音乐的长度。

3.1 Evaluation评价

对C-RNN-GAN的评估是通过对产生的输出进行一些测量来完成的。

复调，测量(至少)两个音调同时演奏的频率(它们的开始时间完全相同)。请注意，这是一个相当有限的度量标准，因为它可以为具有同步音调的音乐提供较低的分数，而这些音调并不是在同一时间开始的。音阶一致性是通过计算作为标准音阶一部分的音调的分数来计算的，并报告这种音阶的最佳匹配数短子序列的重复次数被计数，给出一个样本中有多少重复的分数。这个指标只考虑音调和音调的顺序，而不考虑音调的时间。音调跨度是样本中最低和最高音调之间的半音阶数。我们实现了一个工具来计算这些估计值，该工具与本工作中使用的所有源代码一起可在Github2上获得。

4 Results

实验研究结果如图3所示。对抗性训练帮助模型学习具有更大变异性、更大音调跨度和更大强度跨度的模式。允许模型在每个LSTM单元输出一个以上的音调有助于生成具有更高复调分数的音乐。

4.1听力印象虽然我们还没有对这项工作进行彻底的听力研究，但作者和同事的印象是，经过特征匹配训练的模型比其他变体在结构和惊喜之间获得了更好的平衡。只有最大可能性预训练的版本往往不会给人带来足够的惊喜，而带有小批量特征的版本往往会对结构太少的音乐进行采样，对真正的听众来说是没有兴趣的。这有点令人惊讶，我们打算深入研究。

使用C-RNN-GAN生成的音乐文件可以从http://mogren.one/publications/2016/c-rnn-gan/下载。

5 Discussion and conclusions

在本文中，我们提出了一种用于连续数据的递归神经模型，使用基于生成对抗网络的方法进行训练。虽然还需要做更多的实验，但我们相信结果是有希望的。我们已经注意到，对抗性训练帮助循环神经网络生成的音乐在使用的音调数量和播放音调强度的跨度上变化更大。根据人类的判断，生成的音乐还不能与训练数据中的音乐相比。这其中的原因还有待探究。然而，在评估中(参见图3)，我们可以看到使用C-RNN-GAN生成的音乐分数比使用基线生成的音乐分数更接近真实音乐的分数。生成的音乐是多声部的，但在我们实验评估的复调评分中，测量两个音调在同一时间播放的频率，C-RNN-GAN得分较低。允许每个LSTM单元同时输出最多三个音调，使得模型在复调方面得分更高。

我们可以在生成的样本中听到，虽然每个样本的节奏都有很大的不同，但通常在一个轨道内是相当一致的，在生成的歌曲中给人一种节奏的感觉.