---

前言

1、在每个树行中找最大值、
2、填充每个节点的下一个右侧节点指针、
3、二叉树的最大深度、
4、二叉树的最小深度

---

一、在每个树行中找最大值（力扣515）

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

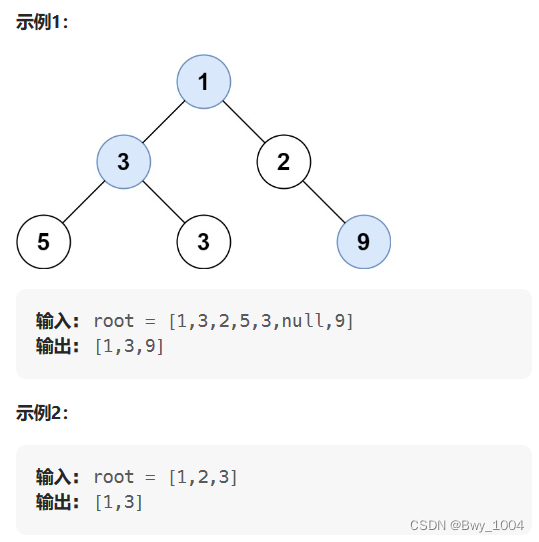
思路：
层序遍历即可，在每一层遍历结束之后搜索最大值

class Solution {
    public List<Integer> largestValues(TreeNode root) {
        List<Integer> resList = new ArrayList<>();
        Queue<TreeNode> que = new LinkedList<>();

        if(root==null){
            return resList;
        }
        que.offer(root);
        while(!que.isEmpty()){
            int len = que.size();
            List<Integer> itemList = new ArrayList<>();
            while(len-->0){
                TreeNode tmpNode = que.peek();
                if(tmpNode.left!=null){
                    que.offer(tmpNode.left);
                }
                if(tmpNode.right!=null){
                    que.offer(tmpNode.right);
                }
                que.poll();
                itemList.add(tmpNode.val);
            }
            int max=Integer.MIN_VALUE;;
            for(int i=0;i<itemList.size();i++){
                if(itemList.get(i)>max){
                    max=itemList.get(i);
                }
            }
            resList.add(max);
        }
        return resList;
    }
}

二、填充每个节点的下一个右侧节点指针（力扣116）

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

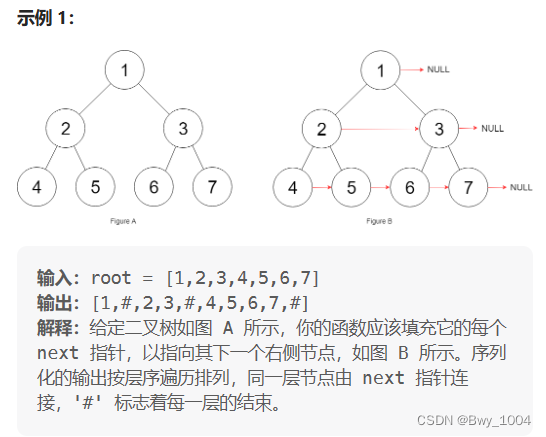
思路：
需要把根节点先单独拿出来，然后再进行后序正常处理即可

class Solution {
    public Node connect(Node root) {
        Queue<Node> tmpQueue = new LinkedList<>();
        if(root!=null){
            tmpQueue.add(root);
        }
        while(!tmpQueue.isEmpty()){
            int len = tmpQueue.size();
            Node cur = tmpQueue.poll();
            if(cur.left!=null){
                tmpQueue.offer(cur.left);
            }
            if(cur.right!=null){
                tmpQueue.offer(cur.right);
            }
            for(int index=1;index<len;index++){
                Node next = tmpQueue.poll(); 
                if(next.left!=null){
                    tmpQueue.offer(next.left);
                }
                if(next.right!=null){
                    tmpQueue.offer(next.right);
                }
                cur.next=next;
                cur=next;
            }
        }
    return root;
    }
}

三、二叉树的最大深度（力扣104）

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

思路：
就是求二叉树的层数
也可以使用递归求解

1、非递归求解

class Solution {
    public int maxDepth(TreeNode root) {
        Queue<TreeNode> que = new LinkedList<>();
        int res = 0;
        if(root==null){
            return res;
        }
        que.offer(root);
        while(!que.isEmpty()){
            int len = que.size();
            while(len-->0){
                TreeNode tmpNode = que.poll();
                if(tmpNode.left!=null) que.offer(tmpNode.left);
                if(tmpNode.right!=null) que.offer(tmpNode.right);
            }
            res++;
        }
        return res;
    }
}

2、递归求解

class Solution {
    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int rightDepth = maxDepth(root.left);
        int leftDepth = maxDepth(root.right);
        return Math.max(rightDepth, leftDepth) + 1;
    }
}

四、 二叉树的最小深度（力扣111）

给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

思路：
求最小深度时将Math.max换成Math.min即可，但要注意如果根节点的左或右子树为空的话是构不成子树的。而最小深度是要求从根节点到子树的。当左或右子树为空时，不符合要求。

class Solution {
    public int minDepth(TreeNode root) {
        if(root==null) return 0;
        if(root.right==null && root.left!=null){
            return 1+minDepth(root.left);
        }
        if(root.left==null && root.right!=null){
            return 1+minDepth(root.right);
        }
        return 1+Math.min(minDepth(root.left),minDepth(root.right));
    }
}

---