正则常见问题及解决方案

news2024/11/19 14:47:59

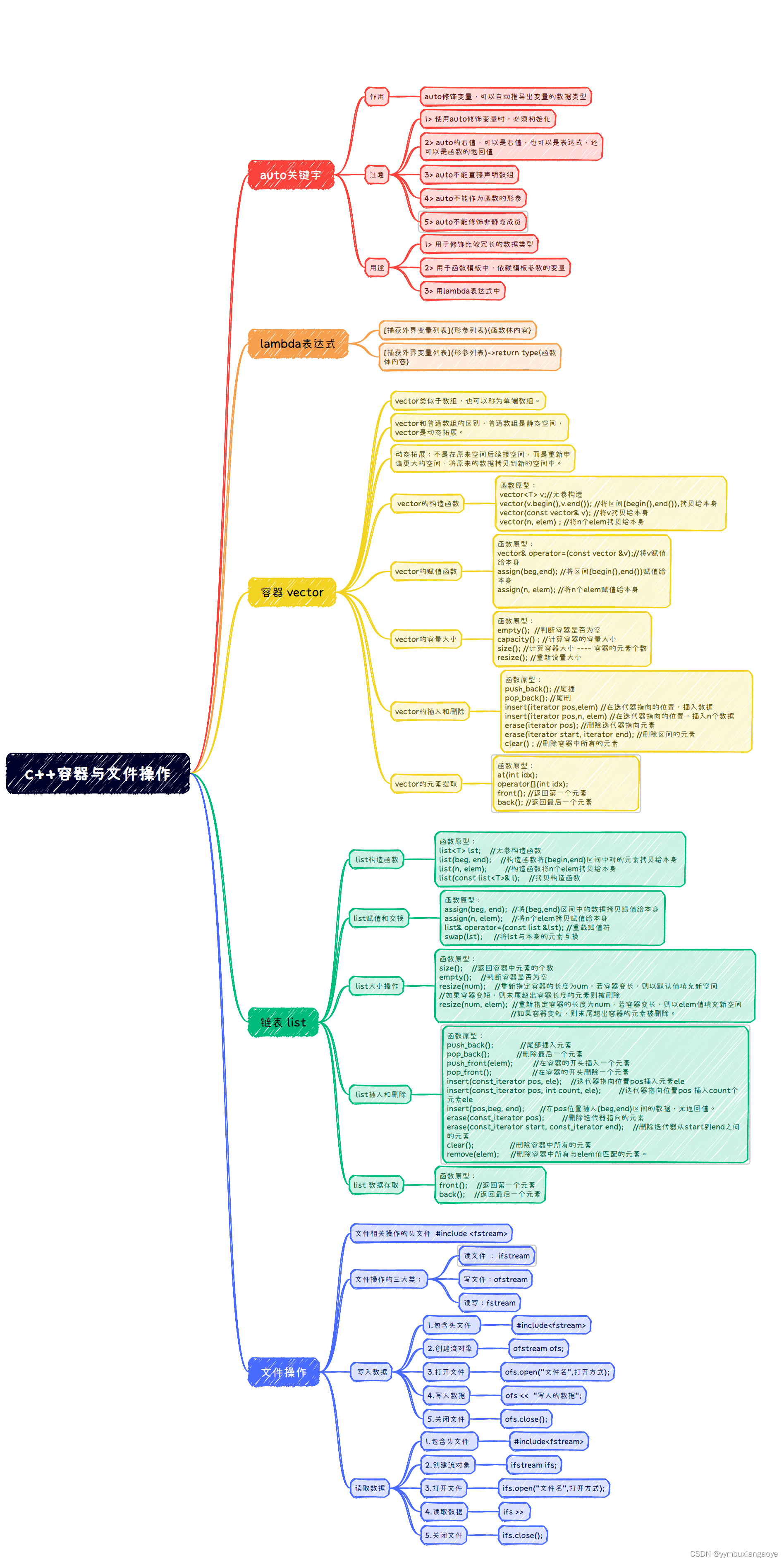
使用正则处理问题的基本思路。有一些方法比较固定，比如将问题分解成多个小问题，每个小问题见招拆招：某个位置上可能有多个字符的话，就⽤字符组。某个位置上有多个字符串的话，就⽤多选结构。出现的次数不确定的话，就⽤量词。对出现的位置有要求的话，就⽤锚点锁定位置。

如果是要查找的内容中不能出现某些字符，这种情况比较简单，可以通过使用中括号来排除字符组，比如非元音字母可以使用 [^aeiou]来表示。

常见问题及解决方案

1、匹配数字

数字的匹配比较简单，通过我们学习的字符组，量词等就可以轻松解决。

数字在正则中可以使用 \d 或 [0-9] 来表示。
如果是连续的多个数字，可以使用 \d+ 或 [0-9]+。
如果 n 位数据，可以使用 \d{n}。
如果是至少 n 位数据，可以使用 \d{n,}。
如果是 m-n 位数字，可以使用 \d{m,n}。

2、匹配正数、负数和小数

如果希望正则能匹配到比如 3，3.14，-3.3，+2.7 等数字，需要注意的是，开头的正负符号可能有，也可能没有，所以可以使用 [-+]? 来表示，小数点和后面的内容也不一定会有，所以可以使用 (?:\.\d+)? 来表示，因此匹配正数、负数和小数的正则可以写成 [-+]?\d+(?:\.\d+)?。

非负整数，包含 0 和正整数，可以表示成[1-9]\d*|0。

非正整数，包含 0 和负整数，可以表示成-[1-9]\d*|0。

3、浮点数

负数浮点数表示：-\d+(?:\.\d+)?。

正数浮点数表示：\+?(?:\d+(?:\.\d+)?|\.\d+)。

4、十六进制数

十六进制的数字除了有 0-9 之外，还会有 a-f（或 A-F）代表 10 到 15 这 6 个数字，所以正则可以写成 [0-9A-Fa-f]+。

5、手机号码

我们可以简单地使用字符组和多选分支，来准确地匹配手机号段。如果只限制前 2 位，可以表示成 1[3-9]\d{9}，如果想再精确些，限制到前三位，比如使用1(?:3\d|4[5-9]|5[0-35-9]|6[2567]|7[0-8]|8\d|9[1389])\d{8}来表示。如果想精确到 4 位，甚至 5 位，可以根据公开的号段信息自己来写一下，但要注意的是，越是精确，只要有新的号段，你就得改这个正则，维护起来会比较麻烦。另外，在实际运用的时候，你可能还要考虑一下有一些号码了 +86 或 0086 之类的前缀的情况。

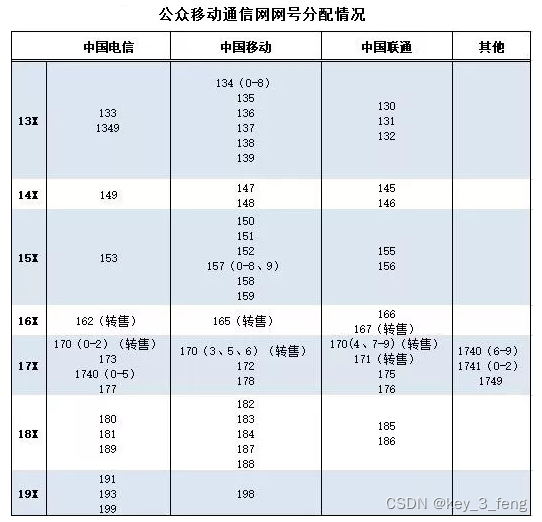
6、身份证号

我国的身份证号码是分两代的，第一代是 15 位，第二代是 18 位。如果是 18 位，最后一位可以是 X（或 x），两代开头都不能是 0，根据规则，你应该能很容易写出相应的正则，第一代可以用 [1-9]\d{14} 来表示，第二代比第一代多 3 位数据，可以使用量词 0 到 1 次，即写成

[1-9]\d{14}(\d\d[0-9Xx])?。

7、邮政编码

邮编一般为 6 位数字，比较简单，可以写成 \d{6}，6 位数字在其它情况下出现可能性也非常大，比如手机号的一部分，身份证号的一部分，所以如果是数据提取，一般需要添加断言，即写成 (?<!\d)\d{6}(?!\d)。

8、腾讯 QQ 号码

目前 QQ 号不能以 0 开头，最长的有 10 位，最短的从 10000（5 位）开始。从规则上我们可以得知，首位是 1-9，后面跟着是 4 到 9 位的数字，即可以使用 [1-9][0-9]{4,9} 来表示。

9、中文字符

中文属于多字节 Unicode 字符，但有一些语言是不支持这种属性的，可以通过另外一个办法，就是码值的范围，中文的范围是 4E00 - 9FFF 之间，这样可以覆盖日常使用大多数情况。

不同的语言是表示方式有一些差异，比如在 Python，Java，JavaScript 中，Unicode 可以写成 \u码值来表示，即匹配中文的正则可以写成 [\u4E00-\u9FFF]，如果在 PHP 中使用，Unicode 就需要写成 \u{码值} 的样式。

10、IPv4 地址

IPv4 地址通常表示成 27.86.1.226 的样式，4 个数字用点隔开，每一位范围是 0-255，比如从日志中提取出 IP，如果不要求那么精确，一般使用 \d{1,3}(\.\d{1,3}){3}就够了，需要注意点号需要转义。

我们可以把 IPv4 表示成 X.X.X.X，可以使用量词，写成 (?:X.){3}X 或 X(?:.X){3}，由于 X 本身比较复杂，里面有多选分支结构，所以需要把它加上括号，所以 IPv4 的正则应该可以写成

(?:1\d\d|2[0-4]\d|25[0-5]|0?[1-9]\d|0{0,2}\d)(?:\.(?:1\d\d|2[0-4]\d|25[0-5]|0?[1-9]\d|0{0,2}\d)){3}。

11、日期和时间

假设日期格式是 yyyy-mm-dd，应该是 \d{4}-(?:1[0-2]|0?[1-9])-(?:[12]\d|3[01]|0?[1-9])。

时间格式比如是 23:34，如果是 24 小时制，小时是 0-23，分钟是 0-59，所以可以写成 (?:2[0-3]|1\d|0?\d):(?:[1-5]\d|0?\d)。

12、邮箱

邮箱的组成是比较复杂的，格式是用户名 @主机名，用户名部分通常可以有英文字母，数字，下划线，点等组成，但其中点不能在开头，也不能重复出现。根据 RFC5322 没有办法写出一个完美的正则，我们可以实现一些简体的版本，比如：[a-zA-Z0-9_.+-]+@[a-zA-Z0-9-]+\.[a-zA-Z0-9-.]+。