【三维重建】【深度学习】NeRF代码Pytorch实现–数据加载(中)

论文提出了一种5D的神经辐射场来作为复杂场景的隐式表示，称为NeRF，其输⼊稀疏的多⻆度带pose的图像训练得到⼀个神经辐射场模型。简单来说就是通过输入同一场景不同视角下的二维图片和相机位姿，对场景进行三维隐式建模，并通过体素渲染方程实现了合成任意新视角下的场景图片。本篇博文将根据代码执行流程解析数据加载过程中具体的功能模块代码。

文章目录

【三维重建】【深度学习】NeRF代码Pytorch实现--数据加载(中)
前言
load_llff_data
spherify_poses
总结

前言

在详细解析NeuS网络之前,首要任务是搭建NeRF【win10下参考教程】所需的运行环境，并完成模型的训练和测试，展开后续工作才有意义。
本博文是对NeuS数据加载过程中涉及的部分功能代码模块进行解析，其他代码模块后续的博文将会陆续讲解。

博主将各功能模块的代码在不同的博文中进行了详细的解析，点击【win10下参考教程】，博文的目录链接放在前言部分。

load_llff_data

load_llff_data在load_llff.py文件内，由于内容太多，博主将这个函数的代码分段进行讲解，本博文将继续讲解load_llff_data函数的后续代码。

# 用于将相机分布限制在固定球体内并返回一个环绕的相机轨迹位姿用于新视角合成。
if spherify:
    poses, render_poses, bds = spherify_poses(poses, bds)

spherify_poses

spherify_poses在load_llff.py文件内，函数代码比较简洁，但内容比较丰富，理解存在难度(博主个人觉得)，比较难理清每行代码乃至每个变量表达的含义和目的，因此博主将函数代码拆分成几段分别讲解，懂得可以快速过。

min_line_dist找到离所有相机中心射线距离之和最短的点，博主找遍了现有网络公开资料也没有发现其具体的原理支持，有知道的朋友可以再评论区留言。

# 让位姿[3×4]变为[4×4]
p34_to_44 = lambda p : np.concatenate([p, np.tile(np.reshape(np.eye(4)[-1, :], [1, 1, 4]), [p.shape[0], 1, 1])], 1)
# 位姿的旋转矩阵R的第三列(z轴相关) 方向向量
rays_d = poses[:, :3, 2:3]  # [N,3,1]
# 位姿的平移矩阵t  相机光心
rays_o = poses[:, :3, 3:4]  # [N,3,1]


# 找到离所有相机中心射线距离之和最短的点
def min_line_dist(rays_o, rays_d):
    A_i = np.eye(3) - rays_d * np.transpose(rays_d, [0,2,1])    # [N,3,3]
    b_i = -A_i @ rays_o         # [N,3,1]
    pt_mindist = np.squeeze(-np.linalg.inv((np.transpose(A_i, [0,2,1]) @ A_i).mean(0)) @ (b_i).mean(0))  # [N,3]
    return pt_mindist

# 简单理解为场景的中心位置
pt_mindist = min_line_dist(rays_o, rays_d)      # [3]
center = pt_mindist

代码的示意图如下图所示：

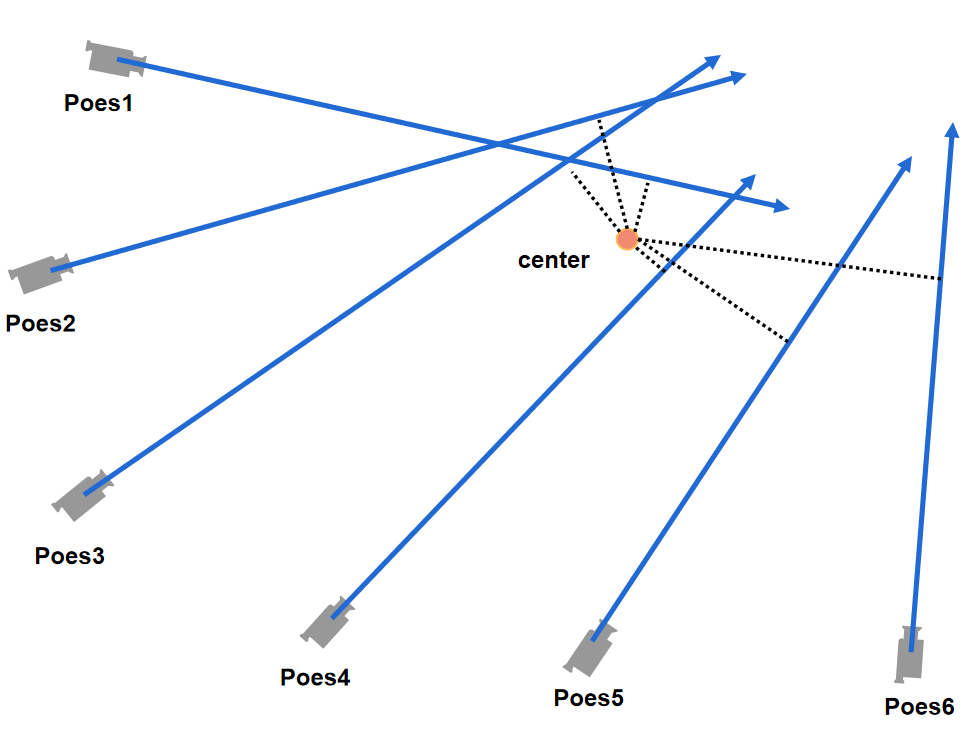
c2w用于中心化相机位姿，这段代码的功能类似于上篇博文的recenter_poses方法，这里不再赘述。

# 所有相机光心到场景中心的方向向量的平均距离向量(xyz轴上)
up = (poses[:, :3, 3] - center).mean(0)     # [3]
# 归一化:平均单位向量
vec0 = normalize(up)    # [3]
# 找到俩俩垂直的单位方向向量
vec1 = normalize(np.cross([.1,.2,.3], vec0))    # [3]
vec2 = normalize(np.cross(vec0, vec1))             # [3]
pos = center
# 构建坐标系
c2w = np.stack([vec1, vec2, vec0, pos], 1)  # [3,4]
# 求c2w的逆矩阵,并与poses进行矩阵运算,目的是完成所有相机位姿的归一化
poses_reset = np.linalg.inv(p34_to_44(c2w[None])) @ p34_to_44(poses[:, :3, :4])      # [N,4,4]

代码的示意图如下图所示：

将所有相机的位置缩放到单位圆内。

# 理解为归一化后所有光心距离的平均
rad = np.sqrt(np.mean(np.sum(np.square(poses_reset[:, :3, 3]), -1)))
# 缩放因子
sc = 1./rad
# 缩放光心
poses_reset[:, :3, 3] *= sc
# 缩放边界
bds *= sc
# 归一化
rad *= sc

代码的示意图如下图所示：

生成新视角的相机位姿。

# 平均光心位置
centroid = np.mean(poses_reset[:, :3, 3], 0)        # [3]
zh = centroid[2]            # 平均光心z轴距离
radcircle = np.sqrt(rad**2-zh**2)
new_poses = []
for th in np.linspace(0., 2.*np.pi, 120):
    camorigin = np.array([radcircle * np.cos(th), radcircle * np.sin(th), zh])
    up = np.array([0, 0, -1.])
    vec2 = normalize(camorigin)
    # 构建坐标系
    vec0 = normalize(np.cross(vec2, up))
    vec1 = normalize(np.cross(vec2, vec0))
    pos = camorigin
    p = np.stack([vec0, vec1, vec2, pos], 1)       # [3,4]
    new_poses.append(p)

# 新视角：拼接在一起
new_poses = np.stack(new_poses, 0)      # [num,3,4]
# [num,3,5] 新视角位姿都拼接了原始位姿的起始位姿
new_poses = np.concatenate([new_poses, np.broadcast_to(poses[0, :3, -1:], new_poses[:, :3, -1:].shape)], -1)
# [num,3,5] 旋转平移后的新位姿都拼接了原始位姿的起始位姿
poses_reset = np.concatenate([poses_reset[:, :3, :4], np.broadcast_to(poses[0, :3, -1:], poses_reset[:, :3, -1:].shape)], -1)