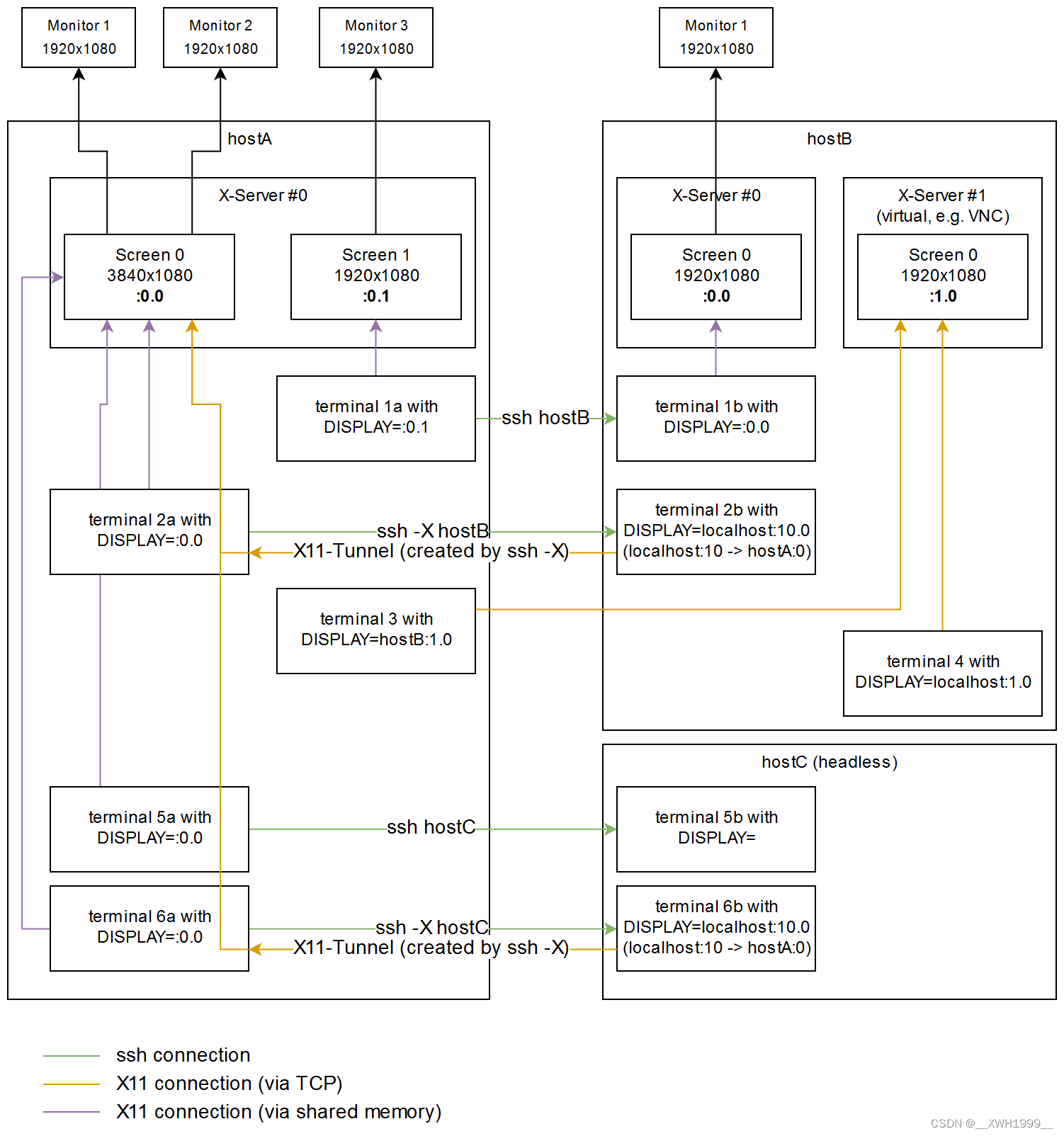
我们之前知道的是里斯表示定理。

这里看到,对于多重线性映射,里斯表示定理会从内积变成混合积。当然我们还是只考虑三维以内的情况。

于是我们可以把不同的1形式和2形式的下标写上,表示他们相当于内积或者混合积对应的那个向量。

然后还差0形式和3形式。0形式就是f本身,而3形式我们知道,就是体形式。也是f加上体形式的微元即可。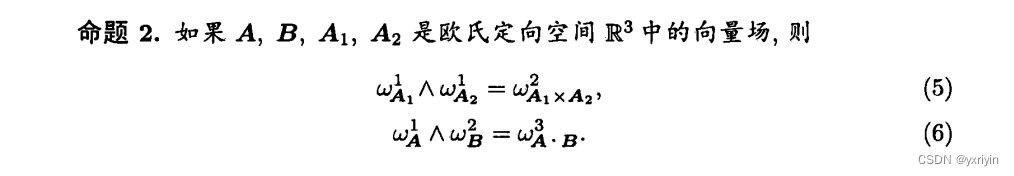
这个命题挺有意思,但等用到的时候我们再看具体是啥吧。

这个就有意思了,f的微分对应的1形式的向量是梯度。一形式下的向量的微分会变成二形式,对应的向量A会变成A的旋度。同样,二形式向量B的微分会变成散度。

这个推导其实没那么好理解。从0形式开始,f, 我们知道,三维下的1形式应该是Pdx1+Qdx2+Rdx3.那么它如果要变成一个内积的形式,应该是<A, x>的内积。我们可以把<A,x>写成<A, dx>x, dx相当于取x的坐标,展开这个内积,就是A1dx1(x) + A2dx2(x) + A3dx3(x)。就是我们的公式(7').同理(8‘)也是这么类似推导得到的。
然后我们再看1形式,他是直接对0形式求微分,那么自然就得到了全微分公式。和公式(7')进行比较,我们自然就得到了A1,A2,A3的值,也就知道了下标A,也就是所谓的梯度的坐标。

同理,我们继续推导旋度,自然也可以得到旋度的坐标表示。

最后是散度。这里其实我们看到每次推导,都是直接用符号A,B,并没有说A就是梯度,B就是旋度。 所以,假设现在有一个2形式,它对应一个向量B,我们可以反推出它的1形式,而这个1形式的向量A,和B之间存在一个关系,B=rotA

因为老师的课程丢失,我们只能自己理解了。有空再看细节吧:最美的公式:你也能懂的麦克斯韦方程组(微分篇) - 知乎

可以看到向量微分算子和梯度算子之间的关系。


这上面用了外微分的乘积微分法则。


这里之前老师也证明过,任何东西,两次微分后都会变成0.证明过程我记得还挺有意思的,但我现在不记得了。注意,微分并不是求导。

这里第一次引出了拉普拉斯算子。是先梯度再散度。

这里可以看到,用哈密顿算子写之前的全部的公式还有一些不错的形式上的结论。这里提到了向量代数,后面也许可以学习一下。

这里把微分1形式和2形式限定在曲线和曲面上的话,就可以用弧长ds和面积元d西格玛来简化书写的形式。
还是要经常回忆下,一般对于普通的黎曼和,我们只需要做出对应的fdx,求和即可。后面可以是微面积对应于多元微积分。但是从微分形式的角度讲,他是将微分形式作用于具体的向量上。然后求和。向量本身看成微元似乎也不太合适。因为微分形式自己就带了具体的dx1,dx2等。现在,我们要进行微分形式的求和和普通黎曼和之间的转化。对于微分形式的求和,因为里面的向量并不是标准笛卡尔坐标系下的,所以我们需要利用拉回映射,把微分形式里的向量换成笛卡尔具体的坐标轴上,例如dxdy.通过拉回映射,我们就能看到微分形式直接作用在笛卡尔坐标轴上,那么得到的自然是标准的微元面积,和黎曼和里面的是一致的。
然后要从1形式开始,其实要从做功开始,应该是<F,dx>的内积,按向量拆开来,就是f1dx1 + f2dx2 + f3dx3,这不就是1形式吗。流形式也是一样的,速度场V和法向量n的内积,再乘以微元,面积微元我们前面推导过了,是普通的二形式的线性组合。

这里用到了一个知识,0形式f直接在两个点上的积分。这个在微分流形章节也是一笔带过,可能要后面系统学习下。

这个结论很有意义,需要记录下。梯度场的功,只和f的等值面有关。

这个结论的物理意义也很重要,向量场沿着曲面边界的环量,其实就是向量A沿着曲线做的功,就等于这个曲线围成的曲面在对应的向量旋度场下的流量。