LeetCode 1. 两数之和（简单）

【题目描述】

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出和为目标值 target 的那两个整数，并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。

【示例1】

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

【示例2】

输入：nums = [3,2,4], target = 6
输出：[1,2]

【示例3】

输入：nums = [3,3], target = 6
输出：[0,1]

【提示】

$2\le nums.length\le 10^4$
$-10^9\le nums[i]\le 10^9$
$-10^9\le target\le 10^9$

【分析】

---

维护一个哈希表，记录 $nums[1]\sim nums[i-1]$，当遍历到 $nums[i]$ 时，通过哈希表查找是否存在 $target-nums[i]$，如果存在说明找到答案。

---

【代码】

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> st;
        for (int i = 0; i < nums.size(); i++)
        {
            int x = target - nums[i];
            if (st.count(x)) return { st[x], i };
            st[nums[i]] = i;
        }
        return {};  // 为了防止编译出问题
    }
};

LeetCode 2. 两数相加（中等）

【题目描述】

给你两个非空的链表，表示两个非负的整数。它们每位数字都是按照逆序的方式存储的，并且每个节点只能存储一位数字。
请你将两个数相加，并以相同形式返回一个表示和的链表。
你可以假设除了数字 $0$ 之外，这两个数都不会以 $0$ 开头。

【示例1】

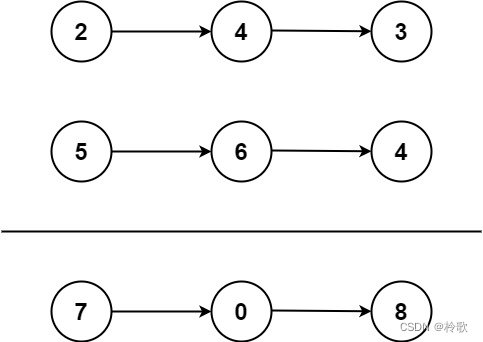
输入：l1 = [2,4,3], l2 = [5,6,4]
输出：[7,0,8]
解释：342 + 465 = 807.

【示例2】

输入：l1 = [0], l2 = [0]
输出：[0]

【示例3】

输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出：[8,9,9,9,0,0,0,1]

【提示】

每个链表中的节点数在范围 $[1,100]$ 内
$0\le Node.val\le 9$
题目数据保证列表表示的数字不含前导零

【分析】

---

模拟题，遍历两个链表，按照高精度加法的思想逐位相加，直到遍历完两个链表且没有进位即可。构造结果链表时可以先创建一个虚拟头结点，返回的时候返回虚拟头结点的下一个结点即可。

---

【代码】

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        auto dummy = new ListNode(-1), cur = dummy;  // 虚拟头结点，cur表示当前指向的结点
        int t = 0;  // 进位
        while (l1 || l2 || t)
        {
            if (l1) t += l1->val, l1 = l1->next;
            if (l2) t += l2->val, l2 = l2->next;
            cur = cur->next = new ListNode(t % 10);  // 记得要更新cur指向下一个结点
            t /= 10;
        }
        return dummy->next;
    }
};

LeetCode 3. 无重复字符的最长子串（中等）

【题目描述】

给定一个字符串 s ，请你找出其中不含有重复字符的最长子串的长度。

【示例1】

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

【示例2】

输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

【示例3】

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
请注意，你的答案必须是子串的长度，"pwke" 是一个子序列，不是子串。

【提示】

$0\le s.length\le 5\ast 10^4$
s 由英文字母、数字、符号和空格组成

【分析】

---

我们枚举所有以 $i$ 为尾端点的子串，分别找出最长的不包含重复字符的子串。因此对于每个 $i$，我们需要找到一个最靠左端点的 $j$，使得 $j\sim i$ 中不包含重复的字符。现在再假设 $i$ 向右移动到 $i^{\prime }$，显然其对应的 $j^{\prime }$ 一定大于等于 $j$，否则通过反证法，$j^{\prime }$ 在 $j$ 的左边且 $j^{\prime }\sim i^{\prime }$ 中不包含重复的字符，那么 $j^{\prime }\sim i$ 中一定也不包含重复的字符。

综上，我们在枚举 $i$ 的时候同样也只需要枚举一遍 $j$，而不需要重复枚举。

---

【代码】

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char, int> st;
        int res = 0;
        for (int i = 0, j = 0; i < s.size(); i++)
        {
            st[s[i]]++;
            while (st[s[i]] > 1) st[s[j++]]--;  // 当j==i时s[i]一定只出现一次了
            res = max(res, i - j + 1);
        }
        return res;
    }
};

LeetCode 4. 寻找两个正序数组的中位数（困难）

【题目描述】

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。
算法的时间复杂度应该为 $O(log(m+n))$。

【示例1】

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

【示例2】

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

【提示】

$nums1.length==m$
$nums2.length==n$
$0\le m\le 1000$
$0\le n\le 1000$
$1\le m+n\le 2000$
$-10^6\le nums1[i],nums2[i]\le 10^6$

【分析】

---

我们求出这两个有序数组中从小到大排第 $k$ 个数是多少即可解决这个问题，当 $k=\frac{n+m}{2}$ 时就是答案。

要解决这个问题我们可以把它分解成子问题，首先我们先分别在这两个数组（记为 $A$ 和 $B$）找到第 $\frac{k}{2}$ 大的数 $A[\frac{k}{2}]$ 和 $B[\frac{k}{2}]$，然后我们分以下三种情况进行讨论：

• $A[\frac{k}{2}]<B[\frac{k}{2}]$：在 $A$ 中小于等于 $A[\frac{k}{2}]$ 的数有 $\frac{k}{2}$ 个，因为 $B[\frac{k}{2}]$ 严格大于 $A[\frac{k}{2}]$，因此在 $B$ 中小于等于 $A[\frac{k}{2}]$ 的数肯定不足 $\frac{k}{2}$ 个。那么小于等于 $A[\frac{k}{2}]$ 的数的数量一定小于 $k$，即 $A[1\sim \frac{k}{2}]$ 一定不会是答案，就可以把这一部分删掉。
• $A[\frac{k}{2}]>B[\frac{k}{2}]$：与第一种情况类似，小于等于 $B[\frac{k}{2}]$ 的数的数量一定小于 $k$，即 $B[1\sim \frac{k}{2}]$ 一定不会是答案，就可以把这一部分删掉。
• $A[\frac{k}{2}]=B[\frac{k}{2}]$：这种情况下 $A[\frac{k}{2}]$ 与 $B[\frac{k}{2}]$ 都可以作为答案，它们都是第 $k$ 大的数，但是由于 $[\frac{k}{2}$ 有可能会比较短的那个数组长度更大，因此不能保证每次两个数组都能取到 $[\frac{k}{2}$ 处，此时随便删去任意一段就行。

综上，我们每次都可以删去 $\frac{k}{2}$ 个数，例如第一轮删去 $A[1\sim \frac{k}{2}]$ 后相当于在 $A[\frac{k}{2}+1\sim m]$ 和 $B[1\sim n]$ 中找第 $k-\frac{k}{2}$ 个数。当 $k=1$ 时即找两个数组的最小值即可。

---

【代码】

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int cnt = nums1.size() + nums2.size();
        if (cnt % 2 == 0)  // 长度为偶数时中位数为中间两个数的平均值
        {
            int l = find(nums1, 0, nums2, 0, cnt / 2);
            int r = find(nums1, 0, nums2, 0, cnt / 2 + 1);
            return (l + r) / 2.0;  // 注意浮点除法
        }
        else return find(nums1, 0, nums2, 0, cnt / 2 + 1);
    }

    // 从nums1的第i个位置以及nums2的第j个位置开始找第k个数
    int find(vector<int>& nums1, int i, vector<int>& nums2, int j, int k)
    {
        // 统一当做nums1是较短的数组来处理
        if (nums1.size() - i > nums2.size() - j) return find(nums2, j, nums1, i, k);
        if (i == nums1.size()) return nums2[j + k - 1];  // nums1为空
        if (k == 1) return min(nums1[i], nums2[j]);
        int a = min(int(nums1.size()), i + k / 2), b = j + (k - k / 2);  // 较短的数组取k/2可能越界
        if (nums1[a - 1] < nums2[b - 1])  // 第一种情况
            return find(nums1, a, nums2, j, k - (a - i));
        else  // 第二和第三种情况
            return find(nums1, i, nums2, b, k - (b - j));
    }
};

LeetCode 5. 最长回文子串（中等）

【题目描述】

给你一个字符串 s，找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

【示例1】

输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

【示例2】

输入：s = "cbbd"
输出："bb"

【提示】

$1\le s.length\le 1000$
s 仅由数字和英文字母组成

【分析】

---

关于最长回文子串的问题有多种解法，最优解法为 Manacher 算法，不过此处不做介绍。

我们枚举回文串的中心点，对于每个中心点设置两个指针分别往左和往右走，找出最长的满足回文的子串，然后维护一个全局最优解即可。

---

【代码】

class Solution {
public:
    string longestPalindrome(string s) {
        string res;
        for (int i = 0; i < s.size(); i++)
        {
            int l = i - 1, r = i + 1;  // 长度为奇数的情况
            while (l >= 0 && r < s.size() && s[l] == s[r]) l--, r++;
            if (res.size() < r - l - 1) res = s.substr(l + 1, r - l - 1);
            l = i, r = i + 1;  // 长度为偶数的情况
            while (l >= 0 && r < s.size() && s[l] == s[r]) l--, r++;
            if (res.size() < r - l - 1) res = s.substr(l + 1, r - l - 1);
        }
        return res;
    }
};