贪心的介绍

贪心的本质是选择每一阶段的局部最优，从而达到全局最优。

例如，有一堆钞票，你可以拿走十张，如果想达到最大的金额，你要怎么拿？

指定每次拿最大的，最终结果就是拿走最大数额的钱。

每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。

再举一个例子如果是有一堆盒子，你有一个背包体积为n，如何把背包尽可能装满，如果还每次选最大的盒子，就不行了。这时候就需要动态规划。因为每次取最大体积的盒子可能导致最终背包有部分位置是空闲的，就无法装满整个背包。

做题的时候，只要想清楚 局部最优 是什么，如果推导出全局最优，其实就够了。

不好意思了，贪心没有套路，说白了就是常识性推导加上举反例。

455.分发饼干

455. 分发饼干

首先对数组g和数组s分别进行升序排序，双指针解法分两种情况：

1.饼干1满足胃口1，两个指针都往后移动一格，且count++

2.饼干1太小无法满足胃口1，遍历g数组的指针j后移，试试更大的饼干能不能满足

class Solution {
    public int findContentChildren(int[] g, int[] s) {
        Arrays.sort(s);
        Arrays.sort(g);
        int count=0;
        int i=0,j=0;
        while(i<g.length&&j<s.length){
            if(s[j]>=g[i]){
                count++;
                i++;
                j++;
            }
            else if(s[j]<g[i]){//饼干不能满足当前小孩，试试下一块饼干
                j++;
            }
        }
        return count;

    }
}

376. 摆动序列（自己会考虑不周全）

本题要考虑三种情况：

1. 情况一：上下坡中有平坡
2. 情况二：数组首尾两端
3. 情况三：单调坡中有平坡

#情况一：上下坡中有平坡

例如 [1,2,2,2,1]这样的数组，如图：

 

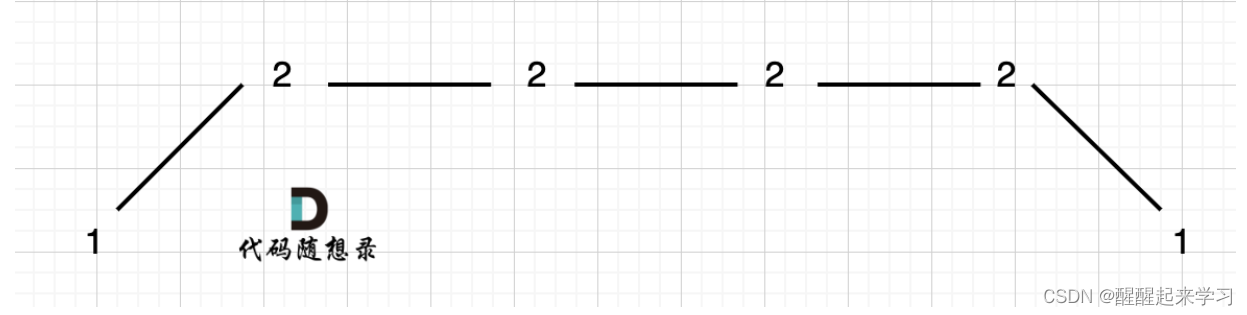
可以统一规则，删除左边的三个 2：

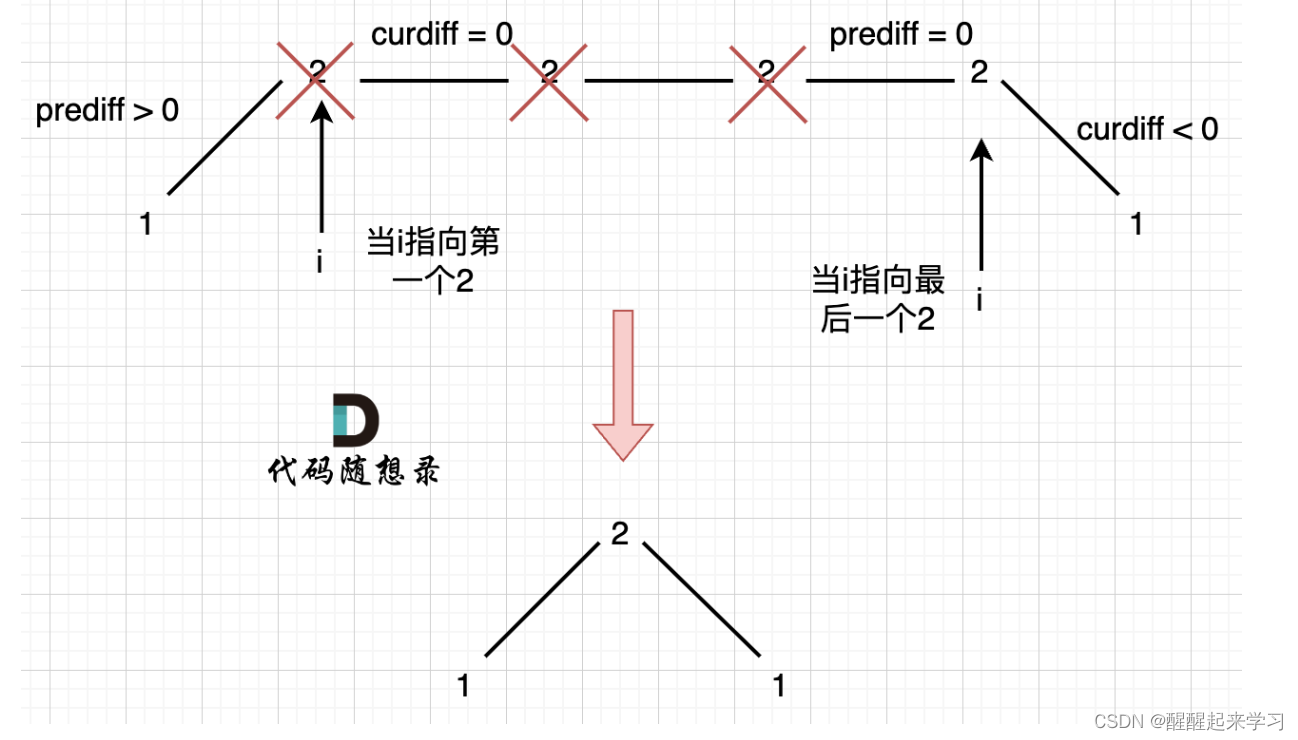
情况二：数组首尾两端

 

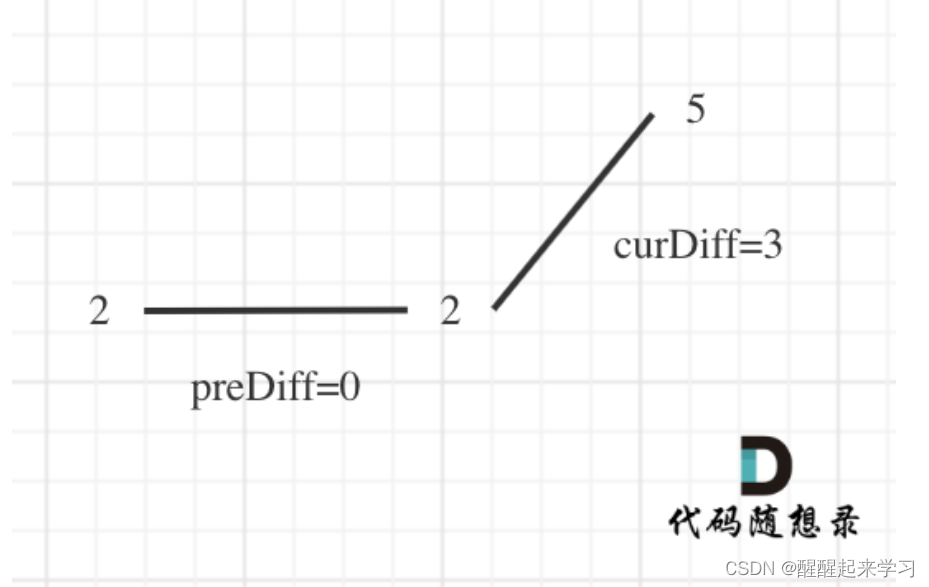
本题统计峰值的时候，数组最左面和最右面如何统计呢？

在 讨论 情况一：相同数字连续 的时候， prediff = 0 ，curdiff < 0 或者 >0 也记为波谷。

针对以上情形，result 初始为 1（默认最右面有一个峰值），此时 curDiff > 0 && preDiff <= 0，那么 result++（计算了左面的峰值），最后得到的 result 就是 2（峰值个数为 2 即摆动序列长度为 2）

情况三：单调坡度有平坡

 

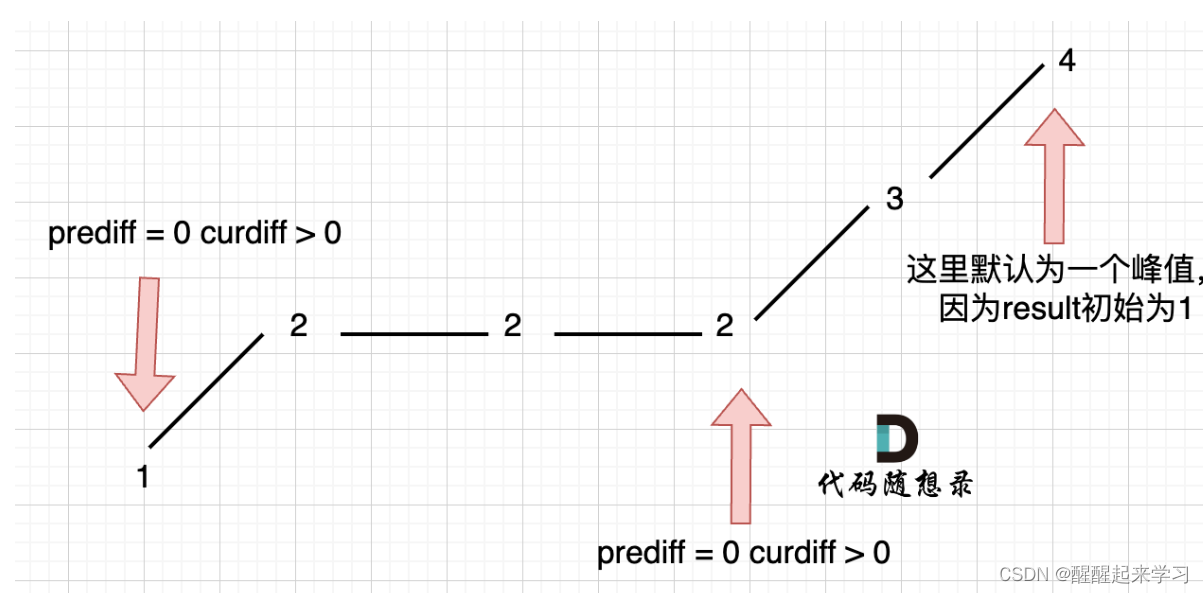
图中，我们可以看出，版本一的代码在三个地方记录峰值，但其实结果因为是 2，因为 单调中的平坡 不能算峰值（即摆动）。

那么我们应该什么时候更新 prediff 呢？

我们只需要在 这个坡度 摆动变化的时候，更新 prediff 就行

代码实现

class Solution {
    public int wiggleMaxLength(int[] nums) {
        //仅有一个元素或者含两个不等元素的序列也视作摆动序列。
        int curDiff=0;//当前的差值
        int preDiff=0;
        int res=1;
        for(int i=0;i<nums.length-1;i++){
            curDiff=nums[i+1]-nums[i];
            //出现峰值
            if((preDiff<=0&&curDiff>0)||(preDiff>=0&&curDiff<0)){
                res++;
                preDiff=curDiff;
            
            }
        }
        return res;

    }
}

53.最大子数组和

这道题是我第二次做了，现在代码基本可以写得出来，就是有一些细节，边界情况要注意；这一次做也加深对贪心的理解

这里把res初始化成最小负数，而不是0。是因为例如有测试用例：【-2，-1】，在之后sum是为负数的，如果res初始化为0，那么是错误的；

代码实现

class Solution {
    public int maxSubArray(int[] nums) {
        if(nums.length==1){return nums[0];}
        //贪心滑动窗口
        int sum=0;
        int res=Integer.MIN_VALUE;//初始化成最小负数，如果
        for(int i=0;i<nums.length;i++){
            sum+=nums[i];
             res=sum>res?sum:res;//注意把这一句放在if条件之前
            if(sum<=0){sum=0;}//sum重新从当前开始，相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
        }
        return res;

    }
}

如果输入用例都是-1，或者 都是负数，这个贪心算法跑出来的结果是 0， 这是又一次证明脑洞模拟不靠谱的经典案例，建议大家把代码运行一下试一试，就知道了，也会理解 为什么 result 要初始化为最小负数了。如下面我最开始写的代码

class Solution {
    public int maxSubArray(int[] nums) {
        //贪心滑动窗口
        int sum=0;
        int res=0;
        for(int i=0;i<nums.length;i++){
            sum+=nums[i];
            if(sum<0){sum=0;}
            res=sum>res?sum:res;
            
        }
        return res;

    }
}

今天贪心第一天，加油！！