打印整数二进制的奇数位和偶数位

获取一个整数二进制序列中所有的偶数位和奇数位，分别打印出二进制序列

思路：
1. 提取所有的奇数位，如果该位是1，输出1，是0则输出0
2. 以同样的方式提取偶数位置

 检测num中某一位是0还是1的方式：
   1. 将num向右移动i位
   2. 将移完位之后的结果与1按位与，如果：
      结果是0，则第i个比特位是0
      结果是非0，则第i个比特位是1

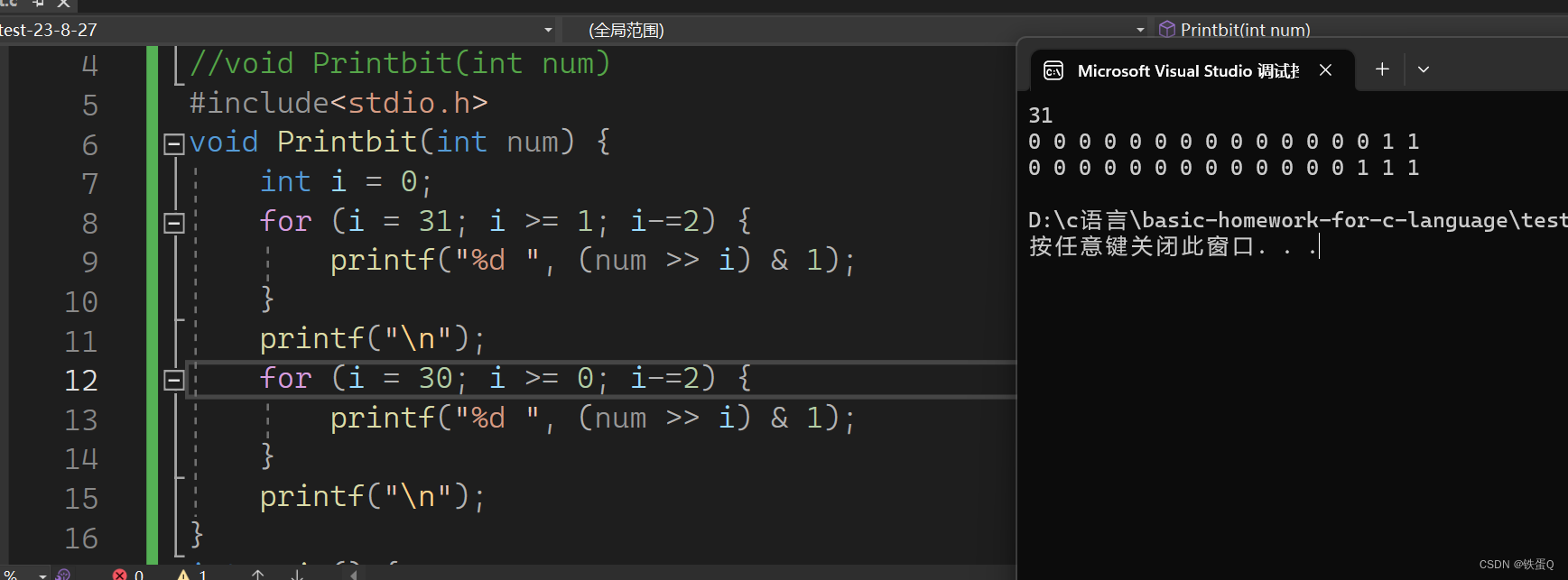
代码：

#include<stdio.h>
void Printbit(int num) {
	int i = 0;
	for (i = 31; i >= 1; i-=2) {
		printf("%d ", (num >> i) & 1);
	}
	printf("\n");
	for (i = 30; i >= 0; i-=2) {
		printf("%d ", (num >> i) & 1);
	}
	printf("\n");
}
int main() {
	void Printbit(int num);
	int num = 0;
	scanf("%d", &num);
    Printbit(num);
	return 0;
}

结果：

 消除因字符串结尾的‘\n’停留在缓存区而对程序产生的影响

方案一：

scanf(" %[^\n]s", arr)，%[^\n]s前面加个空格

方案二：

使用getchar()去掉'\n'