重积分
二重积分计算法: 直角坐标下:化为二次积分 { 如果图形是 X Y 型,则都可以,但要考虑哪个计算不定积分方便 如果图形既不是 X 也不是 Y 型,则要拆分 极坐标下: ∬ f ( x , y ) d x d y = ∬ f ( ρ cos θ , ρ sin θ ) ρ d ρ d θ 三重积分计算法: 利用直角坐标、利用柱面坐标 二重积分计算法:\\ 直角坐标下:化为二次积分 \\ \begin{cases} 如果图形是XY型,则都可以,但要考虑哪个计算不定积分方便 \\ 如果图形既不是X也不是Y型,则要拆分 \end{cases} \\ \,\\ 极坐标下:\\ \iint f(x,y)dxdy=\iint f(\rho\cos\theta,\rho\sin\theta)\rho d\rho d\theta \\ \,\\ 三重积分计算法:\\ 利用直角坐标、利用柱面坐标 二重积分计算法:直角坐标下:化为二次积分{如果图形是XY型,则都可以,但要考虑哪个计算不定积分方便如果图形既不是X也不是Y型,则要拆分极坐标下:∬f(x,y)dxdy=∬f(ρcosθ,ρsinθ)ρdρdθ三重积分计算法:利用直角坐标、利用柱面坐标
重积分的应用(曲面的面积)
【图1】
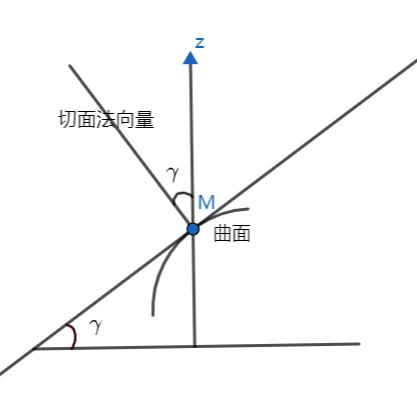
曲面的面积元素的推导过程: 曲面方程为 z = f ( x , y ) 曲面的面积微元可用对应切平面的面积近似代替 如图 1 所示, d A = d σ cos γ , d A 就是曲面的面积微元, d σ 是切平面投影在 x O y 面上的区域 而 cos γ = 1 1 + f x 2 + f y 2 因此 d A = 1 + f x 2 + f y 2 d σ = 1 + f x 2 + f y 2 d x d y 曲面的面积元素的推导过程:\\ 曲面方程为z=f(x,y) \\ 曲面的面积微元可用对应切平面的面积近似代替 \\ 如图1所示,dA=\frac{d\sigma}{\cos\gamma},dA就是曲面的面积微元,d\sigma是切平面投影在xOy面 上的区域 \\ 而\cos\gamma=\frac{1}{\sqrt{1+f_x^2+f_y^2}} \\ 因此dA=\sqrt{1+f_x^2+f_y^2}d\sigma=\sqrt{1+f_x^2+f_y^2}dxdy 曲面的面积元素的推导过程:曲面方程为z=f(x,y)曲面的面积微元可用对应切平面的面积近似代替如图1所示,dA=cosγdσ,dA就是曲面的面积微元,dσ是切平面投影在xOy面上的区域而cosγ=1+fx2+fy21因此dA=1+fx2+fy2dσ=1+fx2+fy2dxdy
曲线积分
对弧长的曲线积分(第一类曲线积分): ∫ L f ( x , y ) d s = ∫ α β f [ φ ( t ) , ψ ( t ) ] φ ′ 2 ( t ) + ψ ′ 2 ( t ) d t ( α < β ) 对坐标的曲线积分(第二类曲线积分,要注意方向): ∫ L P ( x , y ) d x + Q ( x , y ) d y = ∫ α β { P [ φ ( t ) , ψ ( t ) ] φ ′ ( t ) + Q [ φ ( t ) , ψ ( t ) ] ψ ′ ( t ) } d t 线积分与路径无关,只与起点和终点有关 两类曲线积分的关系: ∫ L P d x + Q d y = ∫ L ( P cos α + Q cos β ) d s ∫ Γ A ⋅ d r = ∫ Γ A ⋅ τ d s , A = ( P , Q ) , τ = ( cos α , cos β ) , d r = d s ⋅ τ = ( d x , d y ) 对弧长的曲线积分(第一类曲线积分):\\ \int_Lf(x,y)ds=\int_\alpha^\beta f[\varphi(t),\psi(t)]\sqrt{\varphi ^{\prime2}(t)+\psi^{\prime2}(t)}dt(\alpha<\beta)\\ \,\\ 对坐标的曲线积分(第二类曲线积分,要注意方向):\\ \int_LP(x,y)dx+Q(x,y)dy=\int_\alpha^\beta \{P[\varphi(t),\psi(t)]\varphi^{\prime}(t)+Q[\varphi(t),\psi(t)]\psi^{\prime}(t)\}dt \\ \,\\ 线积分与路径无关,只与起点和终点有关 \\ \,\\ 两类曲线积分的关系:\\ \int_LPdx+Qdy=\int_L(P\cos\alpha+Q\cos\beta)ds \\ \int_\Gamma A\cdot dr=\int_\Gamma A\cdot \tau ds,A=(P,Q),\tau=(\cos \alpha,\cos \beta),dr=ds\cdot \tau=(dx,dy) 对弧长的曲线积分(第一类曲线积分):∫Lf(x,y)ds=∫αβf[φ(t),ψ(t)]φ′2(t)+ψ′2(t)dt(α<β)对坐标的曲线积分(第二类曲线积分,要注意方向):∫LP(x,y)dx+Q(x,y)dy=∫αβ{P[φ(t),ψ(t)]φ′(t)+Q[φ(t),ψ(t)]ψ′(t)}dt线积分与路径无关,只与起点和终点有关两类曲线积分的关系:∫LPdx+Qdy=∫L(Pcosα+Qcosβ)ds∫ΓA⋅dr=∫ΓA⋅τds,A=(P,Q),τ=(cosα,cosβ),dr=ds⋅τ=(dx,dy)
格林公式
定理 1 (格林公式): ∬ D ( ∂ Q ∂ x − ∂ P ∂ y ) d x d y = ∮ L P d x + Q d y 定理 2 (平面上曲线积分与路径无关的条件): ∂ Q ∂ x = ∂ P ∂ y 定理 3 (二元函数的全微分求积): P ( x , y ) d x + Q ( x , y ) d y 为某一函数的全微分的充分必要条件是 ∂ Q ∂ x = ∂ P ∂ y 二元函数全微分求积方法: { 用线积分求 用偏积分求(都能求,比较快) 用凑全微分法求(分组凑微分法,最快,但不一定都能求) 求曲线积分的方法: { 利用参数方程化为二重积分(往往比较复杂) 利用格林公式(补线,围成闭区域) 利用与路径无关,如转换路径,也不用补线了 利用与路径无关、二元函数全微分求积,找出原函数,将起点值和终点值代入原函数相减 定理1(格林公式):\\\iint_D(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y})dxdy=\oint_LPdx+Qdy \\ \,\\ 定理2(平面上曲线积分与路径无关的条件):\\ \frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} \\ \,\\ 定理3(二元函数的全微分求积):\\ P(x,y)dx+Q(x,y)dy为某一函数的全微分的充分必要条件是\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y} \\ \,\\ 二元函数全微分求积方法:\\ \begin{cases} 用线积分求 \\ 用偏积分求(都能求,比较快) \\ 用凑全微分法求(分组凑微分法,最快,但不一定都能求) \\ \end{cases} \\ \,\\ 求曲线积分的方法:\\ \begin{cases} 利用参数方程化为二重积分(往往比较复杂)\\ 利用格林公式(补线,围成闭区域)\\ 利用与路径无关,如转换路径,也不用补线了 \\ 利用与路径无关、二元函数全微分求积,找出原函数,将起点值和终点值代入原函数相减 \end{cases} 定理1(格林公式):∬D(∂x∂Q−∂y∂P)dxdy=∮LPdx+Qdy定理2(平面上曲线积分与路径无关的条件):∂x∂Q=∂y∂P定理3(二元函数的全微分求积):P(x,y)dx+Q(x,y)dy为某一函数的全微分的充分必要条件是∂x∂Q=∂y∂P二元函数全微分求积方法:⎩ ⎨ ⎧用线积分求用偏积分求(都能求,比较快)用凑全微分法求(分组凑微分法,最快,但不一定都能求)求曲线积分的方法:⎩ ⎨ ⎧利用参数方程化为二重积分(往往比较复杂)利用格林公式(补线,围成闭区域)利用与路径无关,如转换路径,也不用补线了利用与路径无关、二元函数全微分求积,找出原函数,将起点值和终点值代入原函数相减
曲面积分
对面积的曲面积分(第一类曲面积分): ∬ f ( x , y , z ) d S = ∬ f [ x , y , z ( x , y ) ] 1 + z x 2 + z y 2 d x d y 对坐标的曲面积分(第二类曲面积分): ∬ Σ P ( x , y , z ) d y d z + Q ( x , y , z ) d x d z + R ( x , y , z ) d x d y ∬ Σ R ( x , y , z ) d x d y = ± ∬ D x y R [ x , y , z ( x , y ) ] d x d y 两类曲面积分的关系: ∬ Σ P d y d z + Q d x d z + R d x d y = ∬ Σ P cos α + Q cos β + R cos γ d S ∬ Σ A ⋅ d S = ∬ Σ A ⋅ n d S = ∬ Σ A n d S , A = ( P , Q , R ) , n 是单位法向量 ( cos α , cos β , cos γ ) , d S = n d S = ( d y d z , d x d z , d x d y ) 为有向曲面元, A n 为 A 在 n 上的投影 归一法: 设曲面可化为 z = f ( x , y ) ,且法向量朝 z 轴正向, 由于 d z d x = − f x , d z d y = − f y 则 ∬ Σ P d y d z + Q d x d z + R d x d y = ∬ Σ { P [ x , y , f ( x , y ) ] ( − f x ) + Q [ x , y , f ( x , y ) ] ( − f y ) + R [ x , y , f ( x , y ) ] } d x d y 当法向量朝 z 轴负向时,其分别为 + f x 、 + f y 、 − 1 或 ∬ Σ P cos α + Q cos β + R cos γ d S = ∬ Σ ( P − f x 1 + f x 2 + f y 2 + Q − f y 1 + f x 2 + f y 2 + R 1 1 + f x 2 + f y 2 ) 1 + f x 2 + f y 2 d x d y 对面积的曲面积分(第一类曲面积分):\\ \iint f(x,y,z)dS=\iint f[x,y,z(x,y)]\sqrt{1+z_x^2+z_y^2}dxdy \\ \,\\ 对坐标的曲面积分(第二类曲面积分):\\ \iint_\Sigma P(x,y,z)dydz+Q(x,y,z)dxdz+R(x,y,z)dxdy \\ \iint_\Sigma R(x,y,z)dxdy=\pm\iint_{D_{xy}}R[x,y,z(x,y)]dxdy \\ \,\\ 两类曲面积分的关系:\\ \iint_\Sigma Pdydz+Qdxdz+Rdxdy=\iint_\Sigma P\cos\alpha+Q\cos\beta+R\cos\gamma dS \\ \iint_\Sigma \textbf{A} \cdot d\textbf{S}=\iint_\Sigma \textbf{A}\cdot \textbf{n}dS=\iint_\Sigma A_ndS,\\ \textbf{A}=(P,Q,R),\textbf{n}是单位法向量(\cos\alpha,\cos\beta,\cos\gamma),\\ d\textbf{S}=\textbf{n}dS=(dydz,dxdz,dxdy)为有向曲面元,A_n为\textbf{A}在\textbf{n}上的投影 \\ \,\\ 归一法:\\ 设曲面可化为z=f(x,y),且法向量朝z轴正向,\\ 由于\frac{dz}{dx}=-f_x,\frac{dz}{dy}=-f_y \\ 则\iint_\Sigma Pdydz+Qdxdz+Rdxdy=\\ \iint_\Sigma \{P[x,y,f(x,y)](-f_x)+Q[x,y,f(x,y)](-f_y)+R[x,y,f(x,y)]\}dxdy \\ 当法向量朝z轴负向时,其分别为+f_x、+f_y、-1 \,\\ 或\\ \iint_\Sigma P\cos\alpha+Q\cos\beta+R\cos\gamma dS= \\ \iint_\Sigma (P\frac{-f_x}{\sqrt{1+f_x^2+f_y^2}}+Q\frac{-f_y}{\sqrt{1+f_x^2+f_y^2}}+R\frac{1}{\sqrt{1+f_x^2+f_y^2}}) \sqrt{1+f_x^2+f_y^2}dxdy 对面积的曲面积分(第一类曲面积分):∬f(x,y,z)dS=∬f[x,y,z(x,y)]1+zx2+zy2dxdy对坐标的曲面积分(第二类曲面积分):∬ΣP(x,y,z)dydz+Q(x,y,z)dxdz+R(x,y,z)dxdy∬ΣR(x,y,z)dxdy=±∬DxyR[x,y,z(x,y)]dxdy两类曲面积分的关系:∬ΣPdydz+Qdxdz+Rdxdy=∬ΣPcosα+Qcosβ+RcosγdS∬ΣA⋅dS=∬ΣA⋅ndS=∬ΣAndS,A=(P,Q,R),n是单位法向量(cosα,cosβ,cosγ),dS=ndS=(dydz,dxdz,dxdy)为有向曲面元,An为A在n上的投影归一法:设曲面可化为z=f(x,y),且法向量朝z轴正向,由于dxdz=−fx,dydz=−fy则∬ΣPdydz+Qdxdz+Rdxdy=∬Σ{P[x,y,f(x,y)](−fx)+Q[x,y,f(x,y)](−fy)+R[x,y,f(x,y)]}dxdy当法向量朝z轴负向时,其分别为+fx、+fy、−1或∬ΣPcosα+Qcosβ+RcosγdS=∬Σ(P1+fx2+fy2−fx+Q1+fx2+fy2−fy+R1+fx2+fy21)1+fx2+fy2dxdy








![java八股文面试[多线程]——为什么不能用Excuters创建线程池](https://img-blog.csdnimg.cn/12962fb3f5e84a90bf837f8d0e3ee7ae.png)