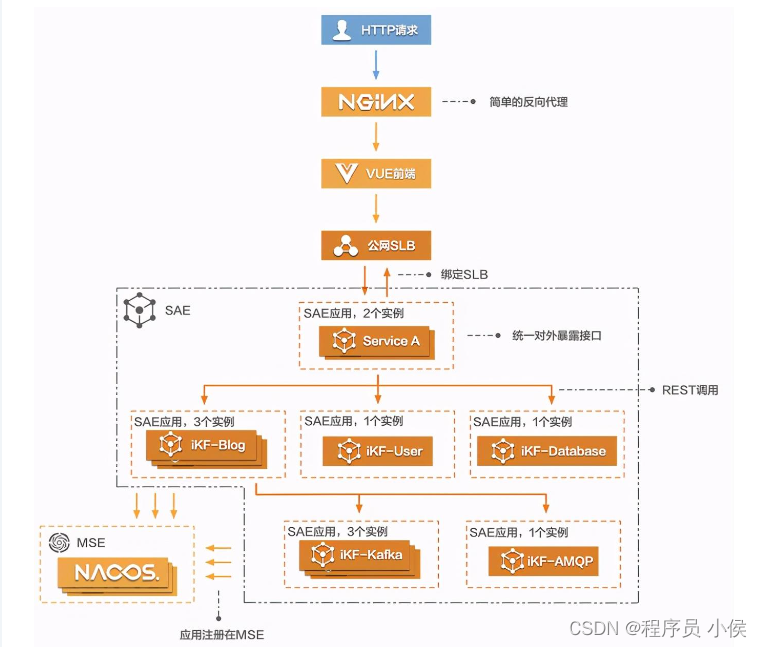
用于C++律动运动的中央模式生成器
一、说明
二、基本概念
中枢模式发生器(CPG)是在动物(包括人类)的中枢神经系统中发现的神经回路或网络。它们负责产生有节奏的运动模式,如行走、游泳或呼吸,而不需要大脑的持续输入。CPG 在控制基本节奏运动方面起着至关重要的作用,它们对于维持协调行为至关重要。
本文中讨论的所有模拟都可以在我的GitHub上找到。
组织为中央模式生成器的简单神经网络的一个例子是半中心振荡器。半中心振荡器由两个神经元组成,它们以交替的方式相互抑制,导致有节奏的模式生成。这种类型的CPG常见于许多动物的运动系统中,如龙虾。
CPG 以其产生协调和有节奏的运动的能力而闻名,这使得它们与软机器人应用高度相关。
让我们以龙虾的口腔胃神经系统为例,它控制着胃磨和幽门肌的节律运动。胃磨机负责咀嚼,而幽门肌则调节食物通过胃的通道。
在这个例子中,我们有两个神经元,神经元A和神经元B,组织成一个半中心振荡器:
- 神经元A:它激活胃磨肌肉并抑制神经元B。
- 神经元B:它激活幽门肌并抑制神经元A。
电路的工作原理如下:
- 最初,神经元A和神经元B都是不活跃的,胃磨和幽门肌处于静止状态。
- 神经元A接受微弱的外部刺激,导致其放电。结果,胃磨肌肉收缩并开始咀嚼运动。同时,神经元A向神经元B发送抑制信号,抑制其活动。
- 由于神经元A的抑制,神经元B变得安静,幽门肌放松,允许食物通过。
- 经过短暂的延迟后,神经元B对神经元A的抑制消失,神经元A再次变得活跃。神经元A开始抑制神经元B,同时激活胃磨肌肉。

结果,幽门肌放松。这个过程以有节奏的模式重复,在神经元A和神经元B之间产生协调的活动循环。肌肉的交替抑制和激活导致胃磨和幽门肌有节奏地运动,产生咀嚼并调节食物通过龙虾胃的通道。
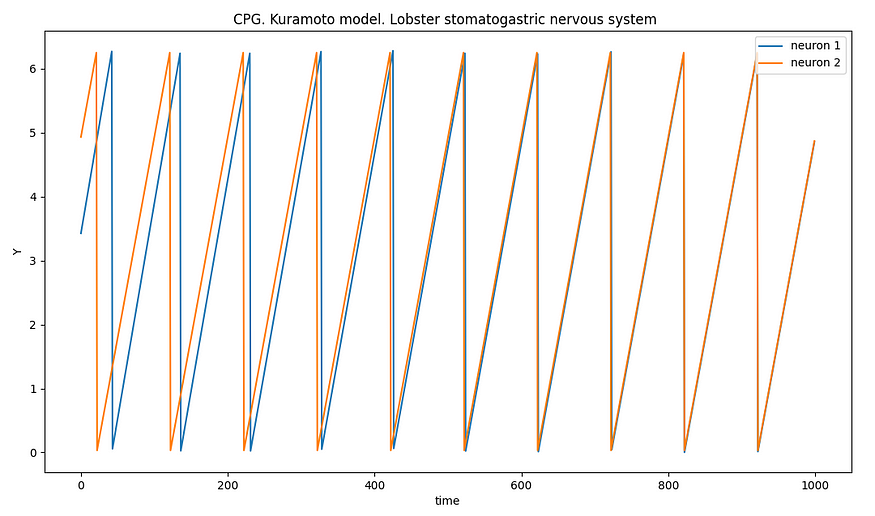
龙虾口腔胃神经系统的模拟(作者)
龙虾口腔胃神经系统中的半中心振荡器只是中枢模式发生器如何控制节律行为的一个例子。CPG的复杂性差异很大,存在于各种动物中,在产生对生存和日常活动至关重要的协调和有节奏的运动方面发挥着重要作用。它们是一个很好的例子,说明神经网络如何在没有来自更高大脑中心的连续输入的情况下生成和控制节奏模式,从而可以有效和自主地控制运动行为。
三、仓本模型
仓本模型是一种数学模型,用于描述耦合振荡器复杂系统中的同步现象。它是由日本物理学家Yoshiki Kuramoto于1975年提出的。该模型的主要思想是研究大量相互作用的振荡器如何随着时间的推移同步它们的相位。
在Kuramoto模型中,每个振荡器都由相位变量θi表示,其中i表示振荡器的指数。相位 θi 表示第 i个振荡器在给定时间的状态。振荡器的动力学由以下一阶微分方程控制:
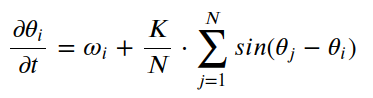
这里:
- ωi 是第 i个振荡器的固有(固有)频率。它表示振荡器在没有与其他振荡器相互作用的情况下的首选频率。
- K是耦合强度,它决定了振荡器之间的相互作用程度。
- N 是系统中振荡器的总数。
该方程描述了每个振荡器的相位θi如何随时间变化。第一项ωi表示固有频率,使振荡器以其固有频率演化。第二学期,
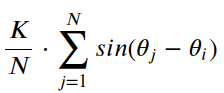
表示与其他振荡器的相互作用。
相互作用项涉及每对振荡器之间相位差的正弦之和。该术语量化了第 i个振荡器受所有其他振荡器相位的影响程度。当振荡器同步时(即它们的相位相似),总和最大化,从而产生更强的同步效果。
在仓本模型中,当耦合强度K足够强时,振荡器之间的相位差往往会随着时间的推移而消失,从而导致同步。随着时间的推移,振荡器会根据与其他振荡器的耦合来调整其相位,最终进入同步状态,其中相位差变为恒定或稳定在特定值。
同步状态对应于集体节奏行为,其中系统中的所有振荡器都锁定在相位中,表现出连贯和协调的运动。这种同步现象是许多自然系统中观察到的共同特征,例如萤火虫闪烁的同步,大脑中神经元的有节奏的放电,或动物群的同步运动。
我们可以使用微分方程组用仓本模型描述三神经元 CPG 网络的行为。每个神经元的(A,B和C)相位将由微分方程表示,该方程描述了相位如何由于其固有频率和与其他神经元的相互作用而随时间变化。
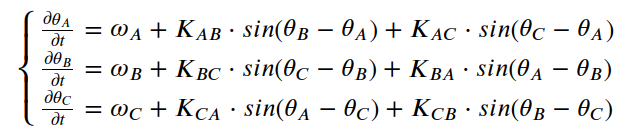
我用龙格-库塔方法找到了微分方程的解。
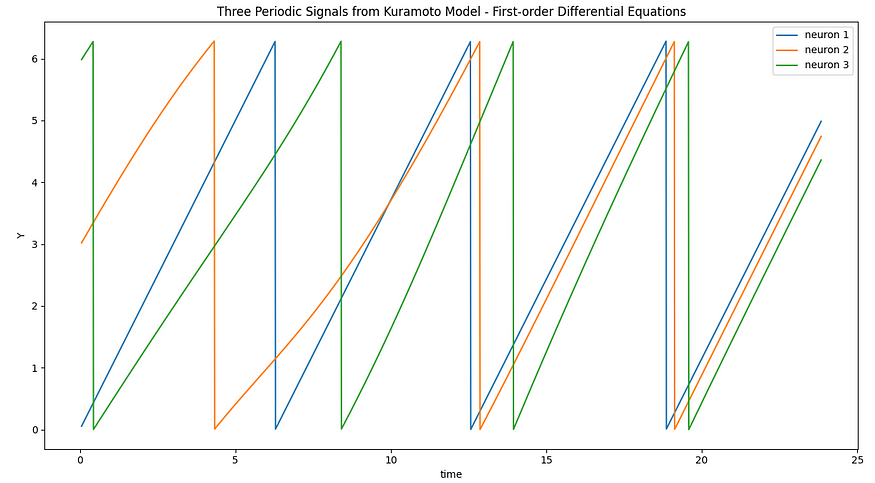
用微分方程描述的CPG模拟(作者)
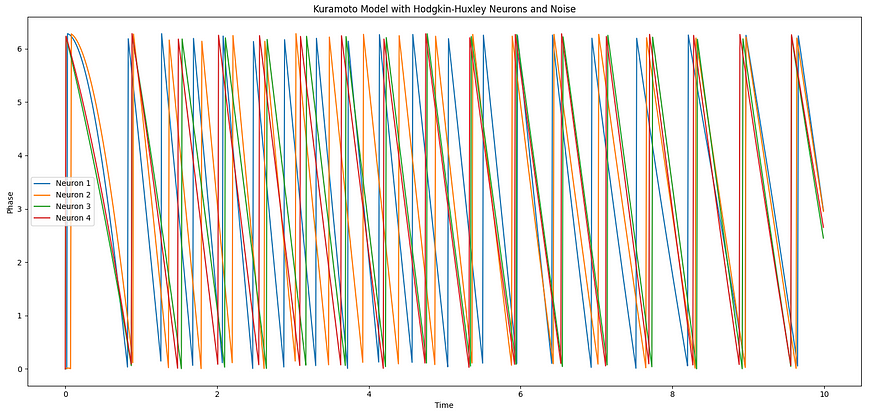
在第一个具有三个神经元的示例中,我们使用带有Hodgkin-Huxley神经元的Kuramoto模型来模拟CPG。霍奇金-赫胥黎模型将动态行为引入神经元,允许它们产生动作电位(尖峰)并表现出复杂的电行为。然后,Kuramoto模型同步这些神经元的相位,导致其活动中的节奏模式。这种节奏模式可以解释为运动神经元在步行机器人中控制腿部运动的有节奏的放电。
在第二个具有多条腿的示例中,我们有一个更复杂的CPG,其中包含多个振荡器,每个振荡器代表机器人的一条腿。我们使用仓本模型和简单的正弦模式进行腿部运动。CPG 为每条腿的运动生成节奏模式,通过调整固有频率、耦合强度、振幅和相位偏移,我们可以创建不同的步行步态,例如步行、小跑或疾驰。机器人的腿以协调和有节奏的方式移动,模仿自然运动中的节奏模式。
总体而言,CPG为机器人系统提供了一种分散的控制机制,使其能够生成有节奏的腿部运动模式,而无需对每条腿进行复杂的中央计算。通过使用CPG,机器人即使在不断变化的环境中也可以实现稳定和自适应的运动模式,并且可以通过相对简单的控制策略行走或移动。
在现实世界的机器人中,CPG通常与感官反馈和其他控制机制相结合,以实现更复杂的运动并适应各种地形条件。CPG 概念提供了一种受生物学启发的方法来控制机器人的腿部运动,使其高效、稳定和多功能。
四、霍奇金-赫胥黎模型
霍奇金-赫胥黎模型是一个数学模型,描述了可兴奋细胞(尤其是神经元)中动作电位的产生和传播。它由Alan Hodgkin和Andrew Huxley于1952年提出,此后成为神经科学中理解神经元和其他可兴奋细胞电行为的基本工具。
霍奇金-赫胥黎模型可用于理解CPG的动力学。在这种情况下,CPG由通过突触连接相互作用的互连神经元组成。CPG中的每个神经元都使用霍奇金-赫胥黎方程建模,该方程描述了在动作电位期间流过神经元膜的离子电流。
霍奇金-赫胥黎模型考虑了以下离子电流:
- 钠(Na+)电流(INa)负责动作电位的快速去极化阶段。
- 钾(K+)电流(IK),负责动作电位的复极化阶段。
- 泄漏电流(IL)代表有助于静息膜电位的小的非特异性离子电流。
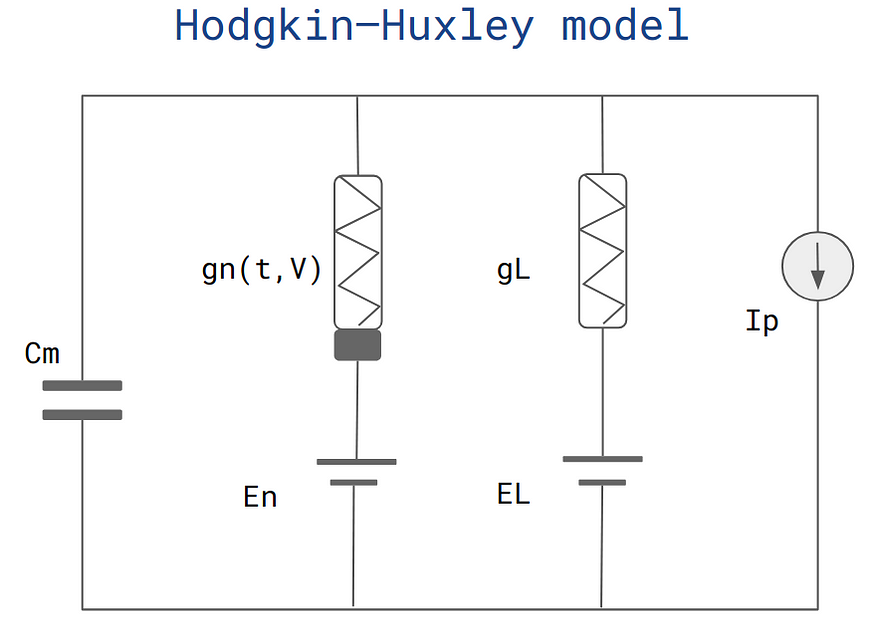
霍奇金-赫胥黎模型(作者)
膜电位(V),
![]()
钠电流,
![]()
钾电流,
![]()
漏电流,
![]()
M门(钠通道的激活门控变量),
![]()
H门(钠通道的失活门控变量),
![]()
N门(钾通道的活化门控变量),
![]()
哪里:
- V是神经元的膜电位。
- C为膜电容。
- I是注入的电流,代表神经元的外部输入。
- gNa、gK 和 gL 分别是钠、钾和泄漏通道的最大电导率。
- M、H 和 N 是门控变量,表示钠和钾的开放离子通道比例。
- ENa、EK和EL分别是钠、钾和泄漏电流的平衡电位。
- alpha_m、beta_m、alpha_h、beta_h、alpha_n和beta_n是控制离子通道门控变量动力学的速率常数。
CPG的动力学由这些神经元之间的相互作用,它们的突触连接以及它们的内在膜特性决定。CPG中的神经元网络通过相互兴奋或抑制连接产生有节奏的活动模式,从而产生协调的节律运动输出。
通过在相互连接的神经元网络中模拟霍奇金-赫胥黎模型,研究人员可以研究不同的连接模式和突触强度如何产生特定的节律运动行为。这对于理解动物如何产生有节奏的运动(如步行或游泳)以及这些模式如何通过感官输入和更高的大脑中枢进行调节尤为重要。
总体而言,霍奇金-赫胥黎模型一直是研究CPG的基础工具,并极大地促进了我们对节律运动行为背后的神经机制的理解。
五、后记
本文是对神经信号、神经动力学的框架构思;其中引进重要的两种模型:仓本模型、霍奇金-赫胥黎模型;以及对模型的内在原理进行探讨。相信以后此类研究将方兴未艾。






![java八股文面试[多线程]——为什么不能用Excuters创建线程池](https://img-blog.csdnimg.cn/12962fb3f5e84a90bf837f8d0e3ee7ae.png)