一、如果用go语言，在一棵比较排序算法的决策树中，一个叶结点可能的最小深度是多少?

文心一言：

在一个排序决策树（如二叉搜索树）中，每个叶节点的最小深度等于输入数据中最大元素与最小元素之间的位距离。这是因为在最坏的情况下，每个比较都需要将最大元素向最小元素的路径移动，因此叶节点的最小深度就是所有元素移动的步数。

对于一个包含n个元素的排序决策树，输入数据中最大元素与最小元素之间的位距离为n，因为每个元素都不同。所以在一棵排序决策树中，一个叶结点的最小深度可能是n。

但是，需要注意的是，这只是一种可能的情况。在实践中，根据数据的分布和排序决策树的具体实现，叶节点的深度可能会更小。

在这里插入图片描述

讯飞星火：

在一棵比较排序算法的决策树中，一个叶结点可能的最小深度是1。因为叶结点是没有子节点的节点，所以它本身就是树的深度。

在这里插入图片描述

360智脑：

在快速排序算法中，一个叶结点可能的最小深度是0。在堆排序算法中，一个叶结点可能的最小深度取决于堆的大小和数据量，一般较小。在比较排序算法的决策树中，一个叶结点可能的最小深度取决于该节点的父节点的值大小以及当前数据的大小和位置等，一般较小。

在这里插入图片描述

chatglm：

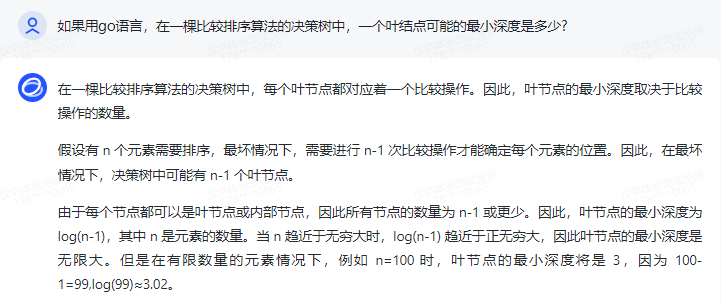
在一棵比较排序算法的决策树中，每个叶节点都对应着一个比较操作。因此，叶节点的最小深度取决于比较操作的数量。

假设有 n 个元素需要排序，最坏情况下，需要进行 n-1 次比较操作才能确定每个元素的位置。因此，在最坏情况下，决策树中可能有 n-1 个叶节点。

由于每个节点都可以是叶节点或内部节点，因此所有节点的数量为 n-1 或更少。因此，叶节点的最小深度为 log(n-1)，其中 n 是元素的数量。当 n 趋近于无穷大时，log(n-1) 趋近于正无穷大，因此叶节点的最小深度是无限大。但是在有限数量的元素情况下，例如 n=100 时，叶节点的最小深度将是 3，因为 100-1=99,log(99)≈3.02。

在这里插入图片描述

通义千问：

在一棵比较排序算法的决策树中，一个叶结点的最小深度取决于排序算法的选择和数据的分布。如果使用快速排序，最坏情况下，一个叶结点的最小深度为n/2，其中n为数据的个数。如果使用归并排序，一个叶结点的最小深度为log_2n。在实际应用中，由于数据的分布往往是随机的，因此一个叶结点的最小深度通常会比最坏情况下的深度要小得多。

在这里插入图片描述

天工：

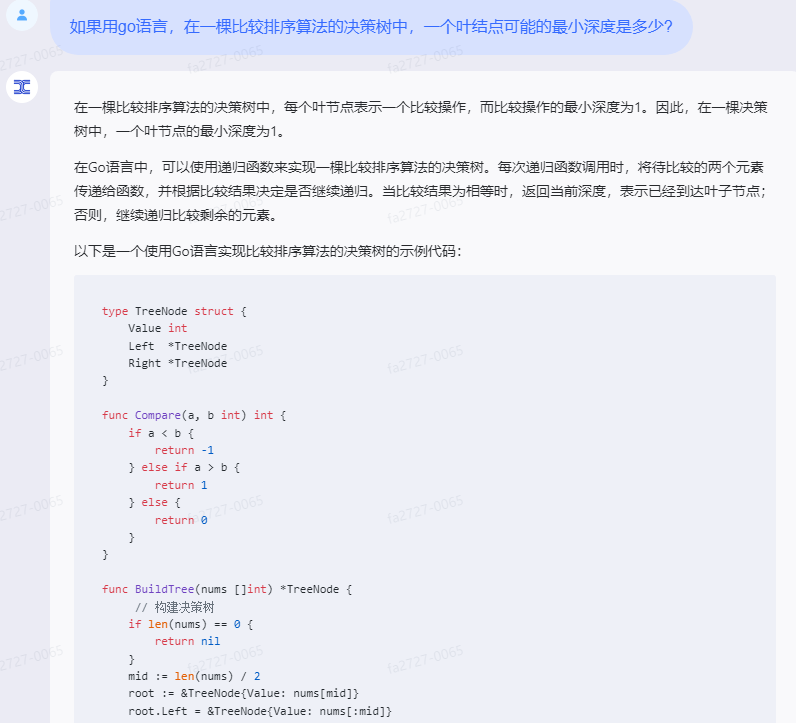
在一棵比较排序算法的决策树中，每个叶节点表示一个比较操作，而比较操作的最小深度为1。因此，在一棵决策树中，一个叶节点的最小深度为1。

在Go语言中，可以使用递归函数来实现一棵比较排序算法的决策树。每次递归函数调用时，将待比较的两个元素传递给函数，并根据比较结果决定是否继续递归。当比较结果为相等时，返回当前深度，表示已经到达叶子节点；否则，继续递归比较剩余的元素。

以下是一个使用Go语言实现比较排序算法的决策树的示例代码：

type TreeNode struct {
    Value int
    Left  *TreeNode
    Right *TreeNode
}

func Compare(a, b int) int {
    if a < b {
        return -1
    } else if a > b {
        return 1
    } else {
        return 0
    }
}

func BuildTree(nums []int) *TreeNode {
     // 构建决策树
    if len(nums) == 0 {
        return nil
    }
    mid := len(nums) / 2
    root := &TreeNode{Value: nums[mid]}
    root.Left = &TreeNode{Value: nums[:mid]}
    root.Right =&TreeNode{Value: nums[mid+1:]}
    return root
}

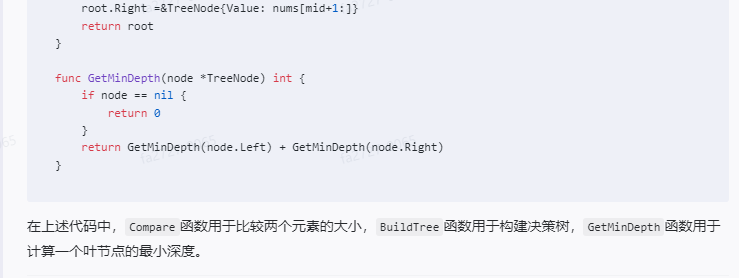
func GetMinDepth(node *TreeNode) int {
    if node == nil {
        return 0
    }
    return GetMinDepth(node.Left) + GetMinDepth(node.Right)
}

在上述代码中，Compare函数用于比较两个元素的大小，BuildTree函数用于构建决策树，GetMinDepth函数用于计算一个叶节点的最小深度。

在这里插入图片描述

chatgpt：

在一棵比较排序算法的决策树中，叶节点的最小深度取决于排序元素的数量。如果有n个元素需要排序，那么在最好的情况下，决策树可以通过完全二叉树来表示，这时叶节点的最小深度是log₂(n+1)。这是因为在完全二叉树中，深度为d的层有2ᵈ个节点，而决策树的叶节点数量为n，所以最小深度可以通过求解2ᵈ ≥ n来得到d的最小值。请注意，这里的深度是基于决策树的层级，而不是基于比较排序算法的操作次数。

在这里插入图片描述