题目描述

 

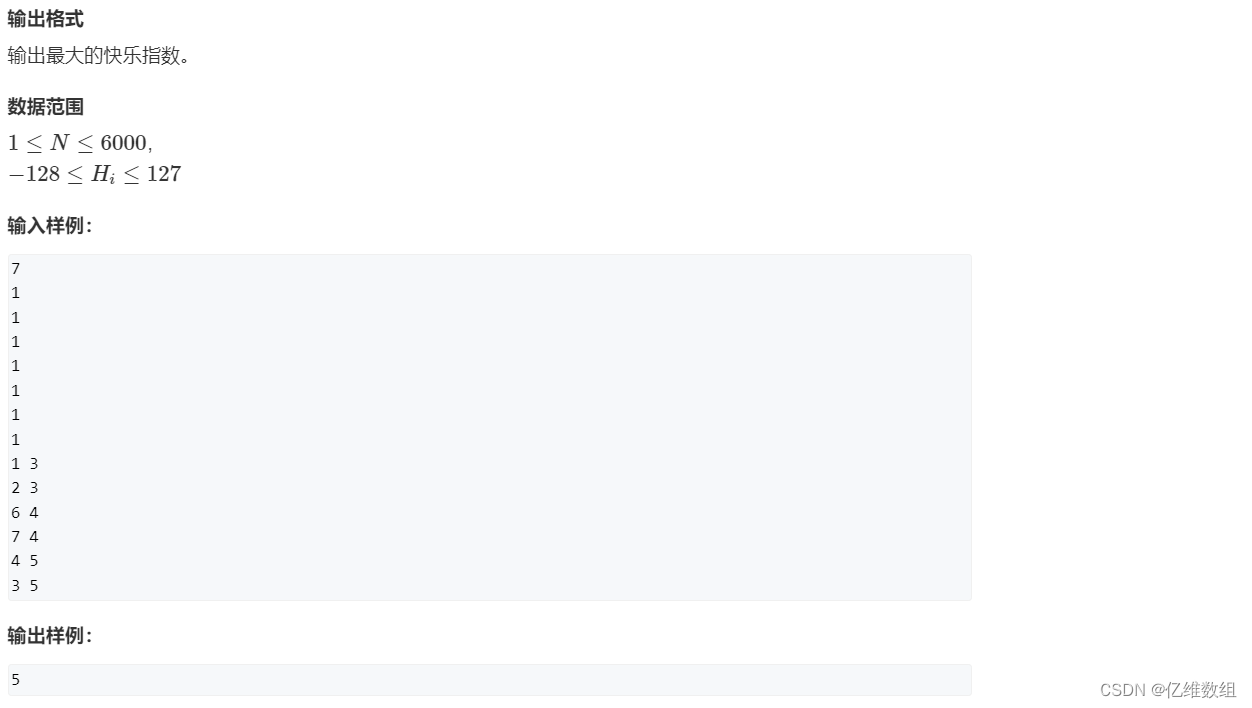
 题目分析

首先来看状态表示：

f[u][1]：所有从以u为根的子树中选择，并且不选u这个点的情况之下的最大指数

f[u][0]：所有从以u为根的子树中选择，并且选择u这个点的情况之下的最大指数

然后看状态计算：

假如选择u这个点，那么u的子节点必然不能选择，得出状态转移式子：

  其中k是u的所有子节点

假如没有选择u这个点，那么u的子节点可以选择也可以不选择，到底选不选，取决于哪种情况下的指数大，易得状态转移式子：

时间复杂度分析：

只需要从父节点开始遍历树上所有结点的子节点，而且已经遍历过的不用重复，而子节点的数量为树的边数n-1，故为O（n）

最后，在acwing中这道题目的题解下面，y总用一句话解释了dfs和dp的区别，一语道破梦中人：

 代码及注释

#include<iostream>
#include<cstring>
using namespace std;
const int N=6010;
int happy[N];
int e[N],ne[N],h[N],idx;
int f[N][2];
int n;
bool has_father[N];//用于寻找根节点
void add(int a,int b)
{
    e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}
void dfs(int u)
{
    f[u][1]+=happy[u];
    for(int i=h[u];i!=-1;i=ne[i])
    {
        int j=e[i];
        dfs(j);//目的是给f[k][1]和f[k][0]赋值，其中k是j以及j所有子孙结点
        f[u][1]+=f[j][0];
        f[u][0]+=max(f[j][0],f[j][1]);
    }
}
int main()
{
    cin>>n;
    memset(h,-1,sizeof h);
    for(int i=1;i<=n;i++)cin>>happy[i];
    for(int i=1;i<n;i++)
    {
        int a,b;
        cin>>a>>b;
        has_father[a]=true;
        add(b,a);
    }
    int root=1;
    while(has_father[root])root++;//寻找根节点
    dfs(root);
    cout<<max(f[root][1],f[root][0])<<endl;
    return 0;
}