❓剑指 Offer 48. 最长不含重复字符的子字符串
难度:中等
请从字符串中找出一个最长的不包含重复字符的子字符串,计算该最长子字符串的长度。
示例 1:
输入: “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
提示:
s.length <= 40000
注意:本题与 3. 无重复字符的最长子串 相同。
💡思路:动态规划
定义 dp 数组,dp[i] 代表以字符 s[i] 为结尾的 “最长不重复子字符串” 的长度。
固定右边界 i ,设字符 s[i] 左边距离最近的相同字符为 s[j] ,即 s[j] = s[i]。
- 当
i < 0,即s[i]左边无相同字符,则dp[i] = dp[i−1] + 1; - 当
dp[i−1] < i - j,说明字符s[i]在子字符串dp[i−1]区间之外 ,则dp[i] = dp[i−1] + 1; - 当
dp[i−1] ≥ i - j,说明字符s[j]在子字符串dp[i−1]区间之中 ,则dp[i]的左边界由s[j]决定,即dp[i] = i − j;
所以 状态转移方程 为:
d
p
[
i
]
=
{
d
p
[
i
−
1
]
+
1
,
i
<
0
d
p
[
i
−
1
]
+
1
,
d
p
[
i
−
1
]
<
i
−
j
i
−
j
,
d
p
[
i
−
1
]
≥
i
−
j
dp[i]=\begin{cases}dp[i-1]+1&,i<0\\dp[i-1]+1&,dp[i-1]<i-j\\i-j&,dp[i-1]\geq i-j\end{cases}
dp[i]=⎩
⎨
⎧dp[i−1]+1dp[i−1]+1i−j,i<0,dp[i−1]<i−j,dp[i−1]≥i−j
观察发现 dp[i] 只与 dp[i - 1] 有关,所以只需定义一个变量 curLen 记录上一个长度。
使用哈希表统计:
- 遍历字符串
s时,使用哈希表(记为preIndexs)统计 各字符最后一次出现的索引位置 。 - 遍历到
s[i]时,可通过访问哈希表preIndexs[s[i]]获取最近上一个的相同字符的索引pre。
🍁代码:(C++、Java)
C++
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int curLen = 0;
int maxLen = 0;
map<char, int> preIndexs;
for(int i = 0; i < s.size(); i++){
int pre = preIndexs.find(s[i]) == preIndexs.end() ? -1 : preIndexs[s[i]]; // 获取当前字符的索引
curLen = curLen < i - pre ? curLen + 1 : i - pre; // dp[i - 1] -> dp[i]
maxLen = max(maxLen, curLen);
preIndexs[s[i]] = i;
}
return maxLen;
}
};
Java
class Solution {
public int lengthOfLongestSubstring(String s) {
int curLen = 0;
int maxLen = 0;
Map<Character, Integer> preIndexs = new HashMap<>();
for(int i = 0; i < s.length(); i++){
int pre = preIndexs.getOrDefault(s.charAt(i), -1); // 获取当前字符的索引
curLen = curLen < i - pre ? curLen + 1 : i - pre; // dp[i - 1] -> dp[i]
maxLen = Math.max(maxLen, curLen);
preIndexs.put(s.charAt(i), i);
}
return maxLen;
}
}
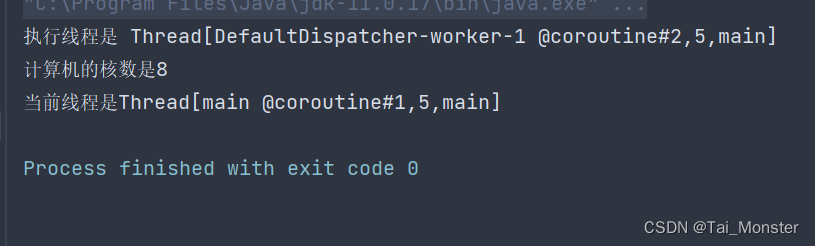
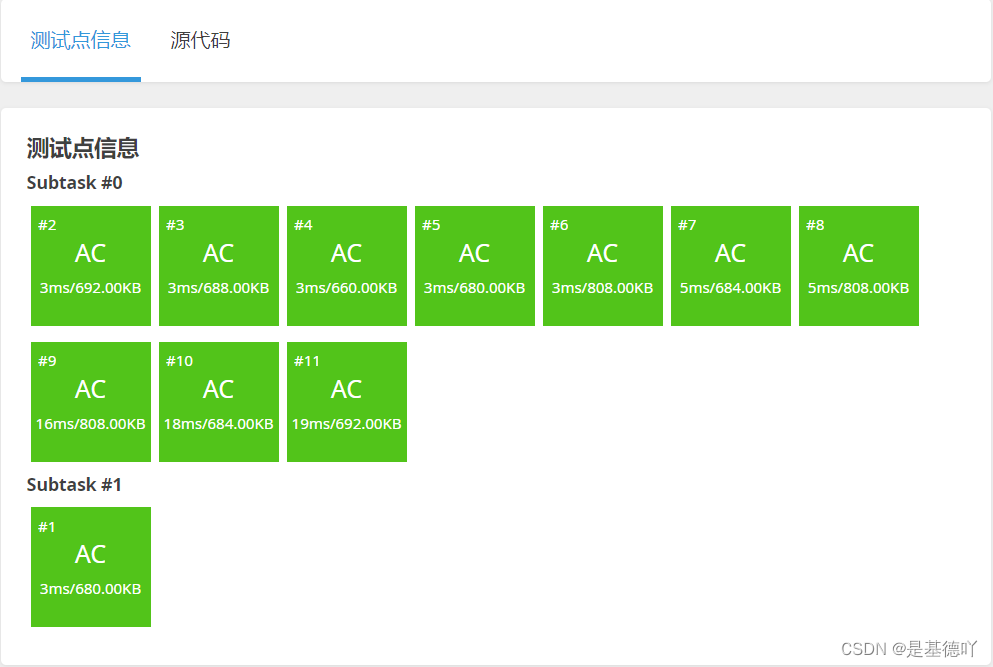
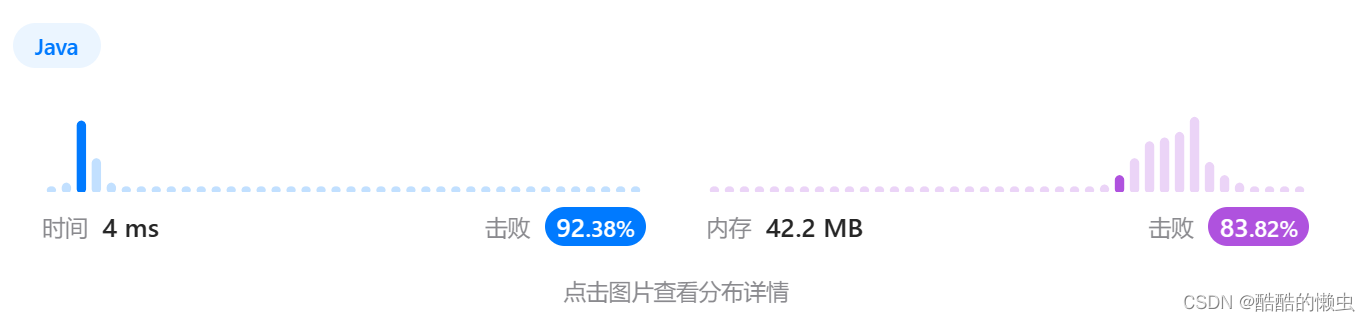
🚀 运行结果:
🕔 复杂度分析:
- 时间复杂度:
O
(
n
)
O(n)
O(n),其中
n为字符串s的长度。 - 空间复杂度:
O
(
1
)
O(1)
O(1),字符的 ASCII 码范围为
0 ~ 127,哈希表preIndexs最多使用 O ( 128 ) = O ( 1 ) O(128)=O(1) O(128)=O(1) 大小的额外空间。
题目来源:力扣。
放弃一件事很容易,每天能坚持一件事一定很酷,一起每日一题吧!
关注我LeetCode主页 / CSDN—力扣专栏,每日更新!