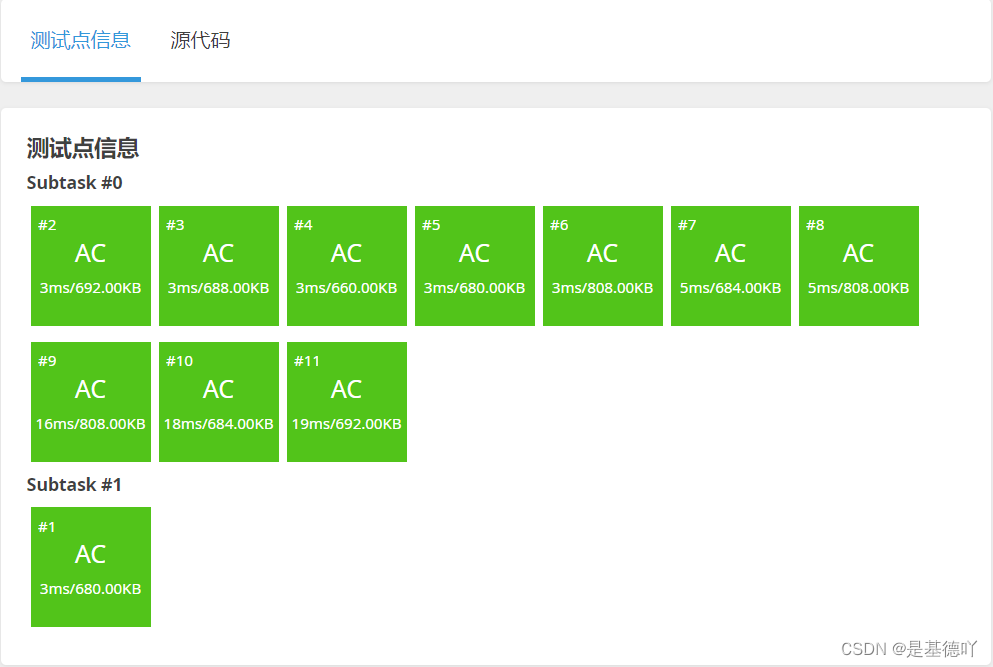
原题链接:https://www.luogu.com.cn/problem/P2678
目录
1. 题目描述
2. 思路分析
3. 代码实现
1. 题目描述

2. 思路分析
二分答案。(使用二分需要满足两个条件。一个是有界,一个是单调。
这题的题面:使得选手们在比赛过程中的最短跳跃距离尽可能长。如果题目规定了“最大值最小”或者“最小值最大”的东西,那么这个东西应该就满足二分答案的有界性和单调性)
定义三个变量d,n,m分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。开一个数组a,数组的第i个元素a[i]表示第i个石头与起点的距离。
定义左边界l=0表示起点的石头,右边界r=d+1,表示终点的石头。
套用二分模板,这里要写一个check()函数。形参x表示当前二分出来的答案。cnt代表计数器,记录以当前答案需要移走的实际石头数。i代表下一块石头的编号。now代表当前跳石头的人所在的位置。
写一个while循环(这里注意循环结束的条件是i<n+1,因为终点那块石头是n+1,而不是n)
判断距离(if(a[i]-a[now]<x)),看二者之间的距离算差值就好。
判定成功,把这块石头拿走(cnt++),继续考虑下一块石头。
判定失败,这块石头不用拿走,我们就跳过去(now=i),再考虑下一块。
3. 代码实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 50010;
int d, n, m, ans;
int a[N];
bool check(int x) {
int cnt = 0;
int i = 0, now = 0;
while (i < n + 1) {
i++;
if (a[i] - a[now] < x) cnt++;
else now = i;
}
if (cnt > m) return false;
else return true;
}
int main() {
cin >> d >> n >> m;
for (int i = 1; i <= n; i++) cin >> a[i];
int l = 0, r = d + 1;
a[0] = 0;
a[n + 1] = d;
while (l + 1 < r) {
int mid = (l + r) / 2;
if (check(mid)) l = mid;
else r = mid;
}
cout << l << endl;
return 0;
}