归并排序
我们先看一下归并排序是怎么归并的
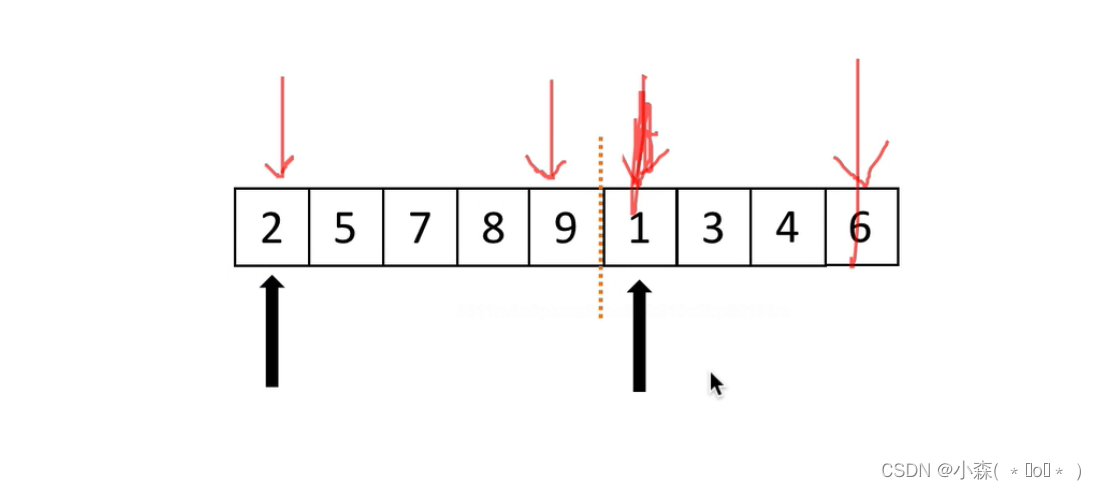
两个有序列表,有low指针指向2,high指针指向6,mid指针指向9
再建一个新列表,1<2,所以1放到列表,右指针右移一位,再比较2和3,2放入列表,左指针右移一位,以此类推,肯定有一部分列表率先没有数,这时将另一列表直接append进入新列表。
def merge(li,low,mid,high):
i=low
j=mid+1
ltmp=[]
while i<=mid and j<=high: # 只要两边都有数
if li[i]<li[j]:
ltmp.append(li[i])
i+=1
else:
ltmp.append(li[j])
j+=1
# 执行完上个while,肯定有一部分没数了
while i<=mid:
ltmp.append(li[i])
i+=1
while j<=high:
ltmp.append(li[j])
j+=1
li[low:high+1]=ltmp对于一个数组,我们将其归并排序的步骤:
>分解:将列表越分越小,直至分成一个元素。
>终止条件:一个元素是有序的。
>合并:讲两个有序列表归并,列表越来越大。
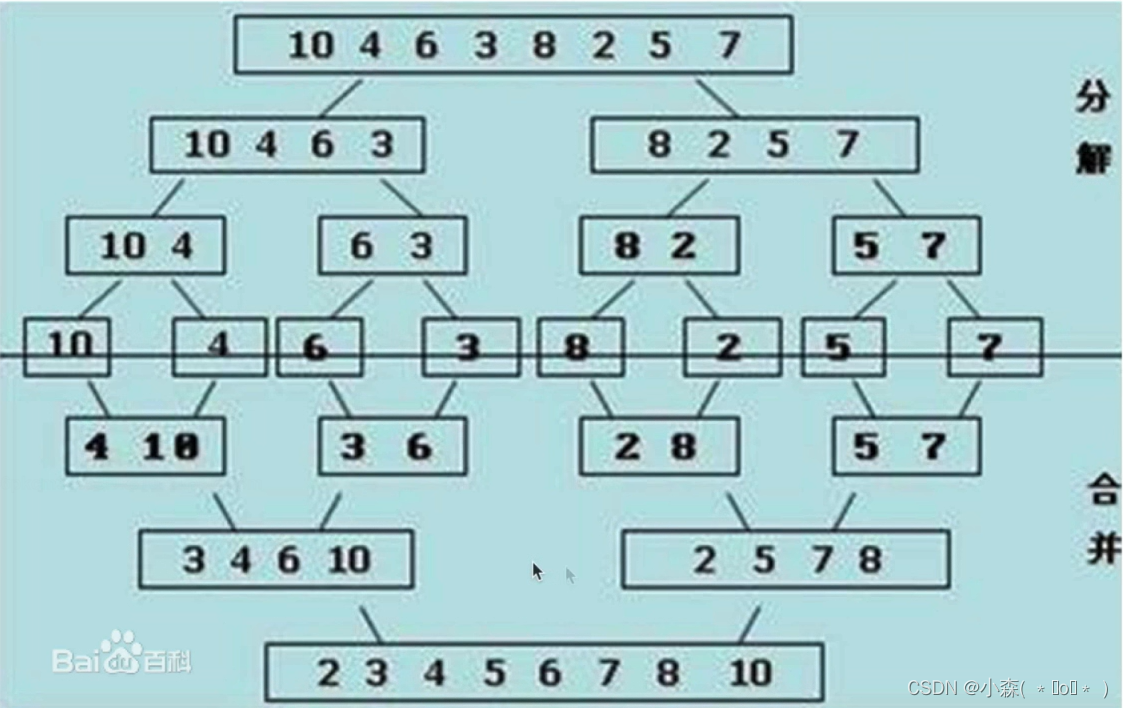
我们可以看出是用递归思想来完成代码
def merge_sort(li,low,high): # 这里递归就是左右,最后左右一起
if low<high: # 至少有两个元素,递归
mid=(low+high)//2
merge_sort(li,low,mid) # 等其递归完成返回一个左侧有序列表
merge_sort(li,mid+1,high) # 等其递归完返回一个右侧有序列表
merge(li,low,mid,high) # 将两个合并
li=list(range(10))
random.shuffle(li)
print(li)
merge_sort(li,0,len(li)-1)
print(li)如果感觉不清楚这个过程,我们可以把递归最后一步merge(li,low,mid,high)改为print打印出来
[4, 7, 2, 8, 10, 13, 12, 6, 1, 11, 3, 5, 9, 0, 14, 15]
[4, 7]
[2, 8]
[4, 7, 2, 8]
[10, 13]
[12, 6]
[10, 13, 12, 6]
[4, 7, 2, 8, 10, 13, 12, 6]
[1, 11]
[3, 5]
[1, 11, 3, 5]
[9, 0]
[14, 15]
[9, 0, 14, 15]
[1, 11, 3, 5, 9, 0, 14, 15]
[4, 7, 2, 8, 10, 13, 12, 6, 1, 11, 3, 5, 9, 0, 14, 15]我们可以看出递归排序是从小到大执行,且从左向右
且归并排序时间复杂度O(nlogn),空间复杂度O(n)
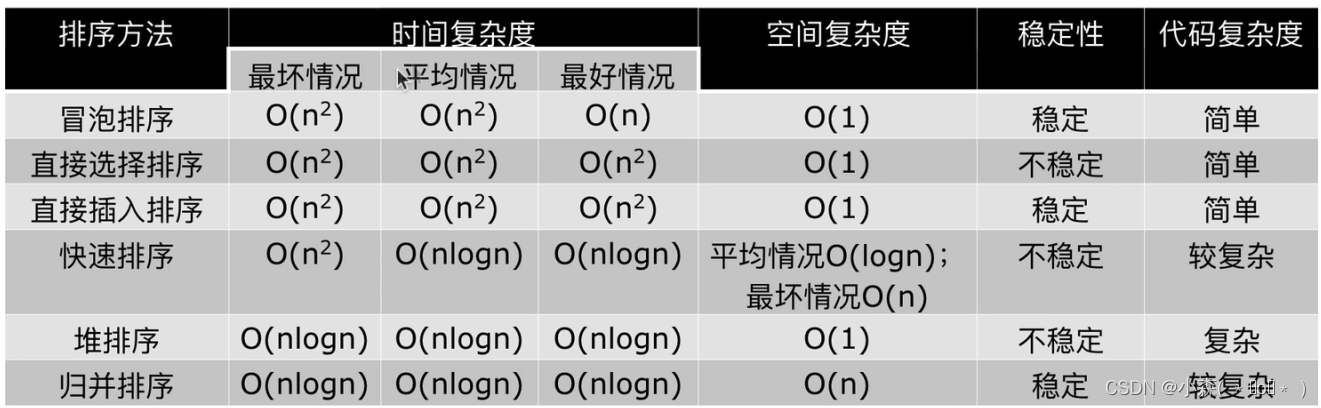
快排,归并,堆排序对比:
一般情况下:快速排序<归并排序<堆排序
三种排序方法的缺点:
快速排序:极端情况下排序效率低
归并排序:需要额外的内存开销
堆排序:在快的排序算法中相对较慢