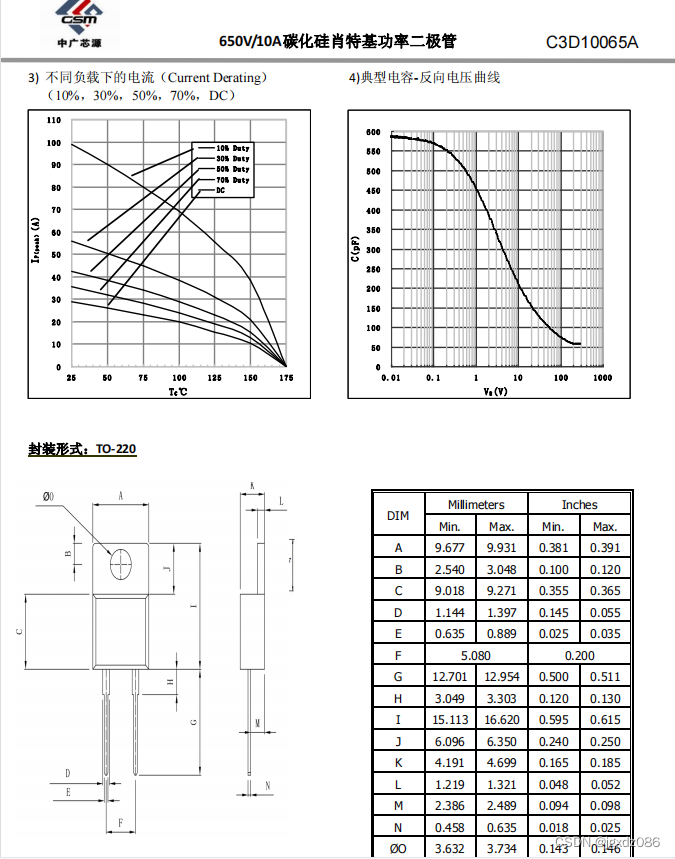
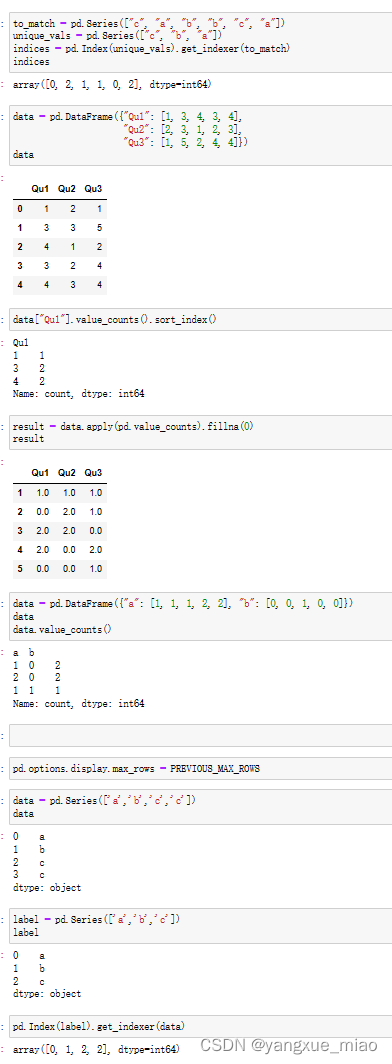
原假设H0：一般是想要推翻的结论，如指标没有变化，实验组和对照组的该结果指标没有差异等。

备择假设H1：一般是想要证明的结论，如实验组的指标是显著提升的，指标提升10%等。

反证法的思想：因为假设检验是反证法的思想，因此说“接受”某假设是不够严谨的，只能说拒绝某假设。如果得出的结论是拒绝原假设，那就说明我们想要证明的结论大概率是正确的。也就是备择假设是显著的，我们达到了预期的目标。

---

 

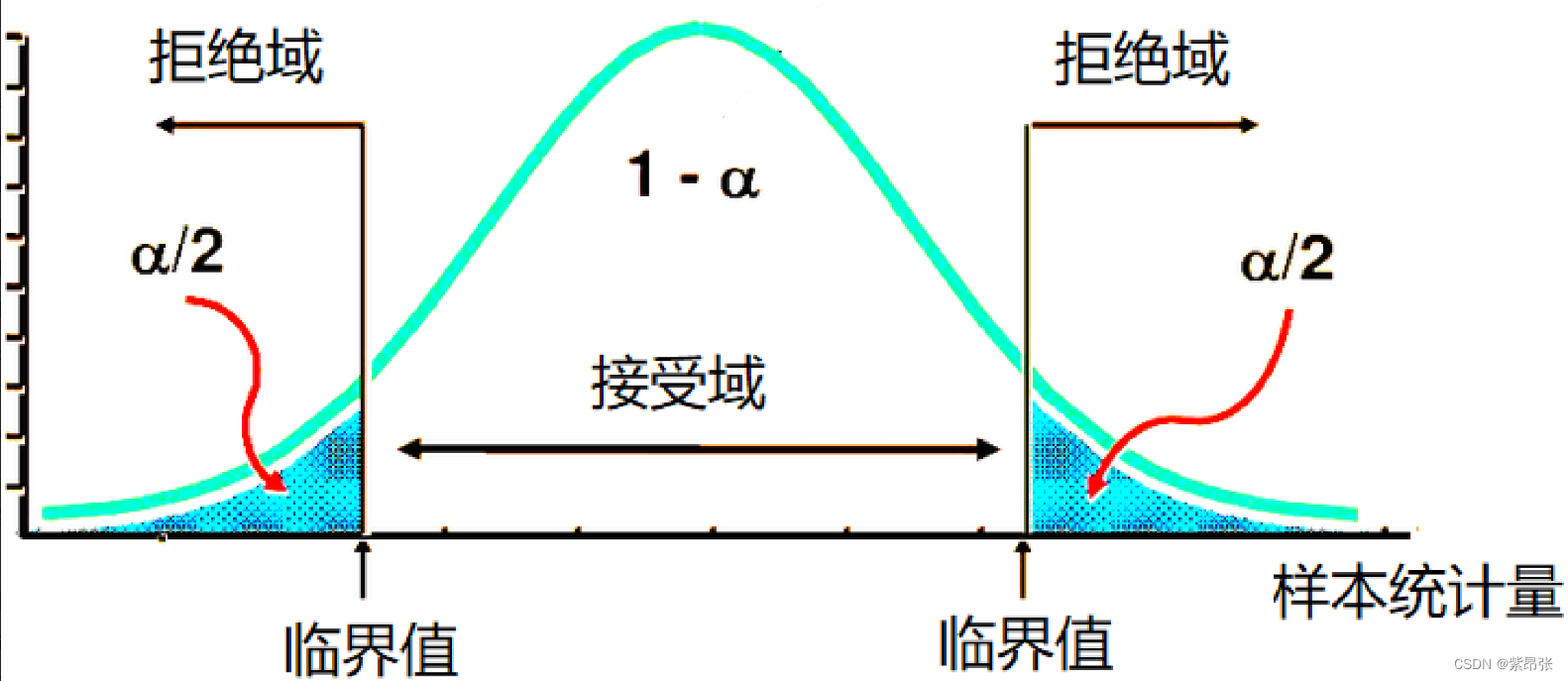
具体例子：

问题	检验方式	H0，H1	原假设H0	备择假设H1
机器生产的产品平均长度为是xx，从产品随机抽n个，问机器是否正常工作	双侧检验	H0:μ≠μ0, H1:μ=μ0	平均长度不等于xx	平均长度等于xx，机器正常工作
从总体抽了n个灯泡，问平均寿命是否大于xx值	右侧检验	H0:μ≤μ0, H1:μ>μ0	平均寿命小于等于xx值	平均寿命大于xx值
从池塘随机抽n条鱼，问是鱼的重量否小于xx值	左侧检验	H0:μ≥μ0, H1:μ<μ0	平均重量大于等于xx值	平均重量小于xx值

假设检验方向的区分 关键看备择假设：

备择假设 H1:μ=μ0, 为双侧假设。

备择假设 H1:μ>μ0, 为右侧假设。

备择假设 H1:μ<μ0, 为左向假设。

---

关键点：

原假设与备择假设是对立事件，两个其中必有一个发生，不可能同时发生，两个事件发生的概率加起来等于1。

假设检验是运用反证法的思想：因为直接证明很麻烦，但用反证法证明原假设H0是小概率事件，则能反向证明备择假设H1的结论是可以被接受的。