DAY1
77. 组合
这道题是经典的回溯题,
递归函数参数和返回值显而易见
终止条件是path.size()==k
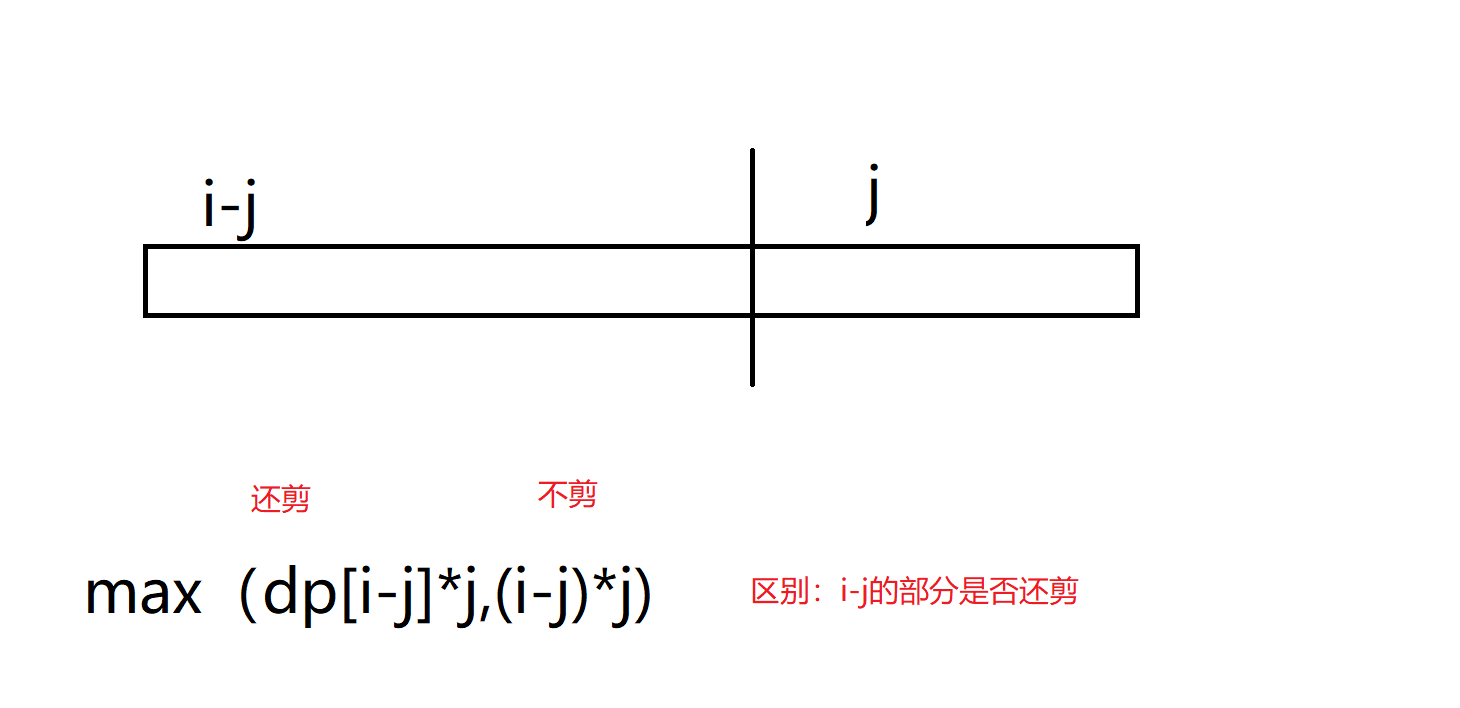
递归逻辑,需要理解每次调用回溯的startIndex的含义,图解:

DAY2
216. 组合总和 III:这道题与77题作类比:
77:1-n,k个数,求组合
216:1-9,k个数,和为n,求组合
此题相比77题思路多了一个要求是求和。其他无二致
1.递归函数:依旧要注意的是当前层的startIndex等于上一层的i+1
2.终止条件:如果当前为第k层且此时path中元素的和等于targetSum,那么将此path添加到res中,(不管当前在第几层)如果当前path中元素的和大于targetSum,return
3.递归逻辑:
与77题基本一致,但是要注意的是回溯的时候要把新加入path的元素移除,同时path元素和要减去移除的元素哦
17. 电话号码的字母组合:第一次做思路完全想不到,只能说第一遍理解思路,争取下次能写一点
DAY3
39. 组合总和:nums数组没有重复元素,每个元素可以重复使用无限次,找出目标和为target的组合
1.递归函数参数和返回值,注意这道题可以先对nums数组进行排序,然后参数中含有startIndex,如果是有序数组,那么再遍历到一处是path元素之和大于target,那么后面就都不用考虑了。
同时要注意当前层的startIndex等于上一层的i,而不用i+1,因为元素是可以无限次使用的
2.递归终止条件:如果此时path中元素的和等于target,那么将此path添加到res中然后return,如果当前path中元素的和大于target,return(相当于剪枝)
3.递归逻辑:和216的递归逻辑一致
40. 组合总和 II:和39相比是每个元素只能用一次,nums中有重复元素,要找出目标和为target的组合,且结果集需要去重
1.递归函数参数和返回值,注意这道题可以先对nums数组进行排序,然后参数中含有startIndex,如果是有序数组,那么再遍历到一处是path元素之和大于target,那么后面就都不用考虑了。
同时要注意当前层的startIndex等于上一层的i+1(这是和39题的一个小区别),因为每个元素只能使用1次
2.递归终止条件:同39题
3.递归逻辑:这里涉及到去重操作,引入一个used数组,因为同一树层不可以有相同元素,但是同一树枝可以有,我们通过used[i-1]来判断是在树枝还是树层遍历了相同元素,如果used[i-1]是false说明就是同一树层,否则说明是在树枝。是怎样理解的呢?
因为如果一直递归一直递归就说明是在同一树枝,used[i]始终是true,当回溯到上一个树层时候才会有used[i]=false
还是有很多要思考的地方
131. 分割回文串
这道题要思考的点是:切割+判断是否为回文串
这道题学到的是关于回溯是如何调用的,
下面是个人理解的回溯调用过程(有问题望指正,感激不尽)

DAY4
93. 复原 IP 地址:分割字符串成4个子串,每个子串要判断是否符合IP规范(写一个isValid方法 )
1.递归函数:当前层的startIndex是上一层的i+2(要考虑逗点的存在)
2.终止条件:如果分割次数==3,说明已经完成了分割成4个子串的任务,同时要检查最后一个子串是否有效,是则将其添加到path,否则return。
3.递归逻辑:注意逗点的插入会影响下一次递归的初始下标
isValid()方法:开头为0的字段不行,大小超过255的字段不行
78. 子集:nums中元素互不相同,求不重复的所有子集(包括空集)。求取子集问题,不需要任何剪枝,因为子集就是要遍历整棵树。
1.递归函数,参数是nums数组和startIndex,返回值是void
2.终止条件,当剩余集合为{}即,startIndex>=nums.length时,说明没有元素可取了
3.递归逻辑,注意点是元素不重复取,因此backtracking(nums,i+1);注意这里的i+1
90. 子集 II:和79题区别是nums可能包含重复元素,求不重复的所有子集(包括空集)。本题要解决:去重+组合
强调去重就要对nums数组排序,方便记录当前树层是否使用相同元素,如果使用了,要跳过
做完这道题回头看40.也可以不必用到used数组
DAY5
491. 递增子序列:找出所有该数组中不同的递增子序列,递增子序列中 至少有两个元素。
这道题不能对原数组nums进行sort,
1.递归函数:求子序列,很明显一个元素不能重复使用,所以需要startIndex,调整下一层递归的起始位置
2.终止条件:如果是path.size()>1那么添加到结果集res中;也可以不加终止条件,startIndex每次都会加1,并不会无限递归。
3.递归逻辑:这里需要一个去重判断,同一父节点下的同层上使用过的元素就不能再使用了
46. 全排列: 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列
这道题的for循环每次i=0开始
1.递归函数
首先排列是有序的,也就是说 [1,2] 和 [2,1] 是两个集合,需要一个used数组标记已经选择的元素
2.终止条件
如果path的大小等于nums的长度,加入到res并return
3.递归逻辑
注意这里的for循环每次从0开始,因为这里要找的是全排列
47. 全排列 II:相比46题,这道题nums数组中可能有重复元素,因此需要去重,如果
1.递归函数
需要used数组判断始终同树枝还是同层遇到相同元素
2.终止条件
同46题
3.递归逻辑
同层不能选相同的数字
used[i - 1] == true,说明同一树枝nums[i - 1]使用过
used[i - 1] == false,说明同一树层nums[i - 1]使用过,要跳过
同时要判断used[i]是否为false,为false才说明是同树枝才能够将当前元素添加到path中
还没写完,就是说需要把每道题的回溯过程整理一遍,但今天好累,先这样明天再来。