目录
一. 查找的基本概念
二. 线性表的查找
(1)顺序查找(线性查找)
(2)折半查找(二分或对分查找)
(3)分块查找
一. 查找的基本概念
查找表是由同一类型的数据元素(或记录)构成的集合。由于“集合”中的数据元素之间存在着松散的关系,因此查找表是一种应用灵便的结构。例如:每个同学的考号和成绩。
查找——根据给定的某个值,在查找表中确定一个其关键字等于给定值的数据元素或(记录)。
关键字用来标识一个数据元素(或记录)的某个数据项的值。
- 主关键字:可唯一地标识一个记录的关键字是主关键字;(如:准考证号,每个准考证号唯一确定一名考生)
- 次关键字:反之,用以识别若干记录的关键字是次关键字。(如:物理成绩,可能物理同一分数有很多人)
若查找表中存在这样一个记录,则称“查找成功”。查找结果给出整个记录的信息,或指示该记录在查找表中的位置;否则称“查找不成功”。查找结果给出“空记录”或“空指针”。
对查找表经常进行的操作:
- 查询某个“特定的”数据元素是否在查找表中;
- 检索某个“特定的”数据元素的各种属性;
- 在查找表中插入一个数据元素;
- 删除查找表中的某个数据元素。
查找表可以分为两类。静态查找表是仅作查询”(检索)操作的查找表。动态查找表是作"插入”和“删除”操作的查找表。有时在查询之后,还需要将查询结果为“不在查找表中”的数据元素插入到查找表中;或者,从查找表中删除其“查询”结果为“在查找表中”的数据元素,此类表为动态查找表。
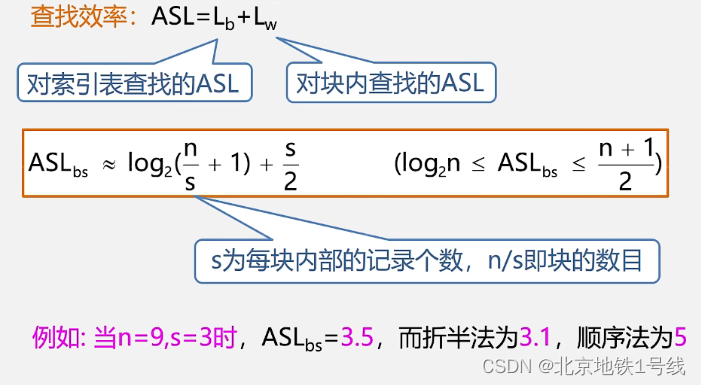
查找算法的评价指标:关键字的平均比较次数,也称平均查找长度ASL(Average Search Length);其中:n:记录的个数;pi:查找第i个记录的概率(通常认为pi =1/n);ci:找到第i个记录所需的比较次数;
查找的方法取决于查找表的结构,即表中数据元素是依何种关系组织在一起的。由于对查找表来说,在集合中查询或检索一个“特定的”数据元素时,若无规律可循,只能对集合中的元素一一加以辨认直至找到为止。而这样的“查询”或“检索”是任何计算机应用系统中使用频度都很高的操作,因此设法提高查找表的查找效率,是本节讨论问题的出发点。为提高查找效率,一个办法就是在构造查找表时,在集合中的数据元素之间人为地加上某种确定的约束关系。
二. 线性表的查找

(1)顺序查找(线性查找)
应用场景:顺序表或线性链表表示的静态查找表,表内元素之间无序。
数据元素类型定义如下:
typedef struct{
KeyType key; //关键字域
int math; //其他域
}ElemType;
typedef struct { //顺序表结构类型定义
ElemType *R; //表基址
int length; //表长
}SSTable; //Sequential Search Table
SSTable ST; //定义顺序表ST
我们从后往前比较,不难写出顺序查找的算法:

int Search_Seq(SSTable ST, KeyType key){ //Keytype根据问题需要自己设置
//若成功返回其位置信息,否则返回0
for(i=ST.length; i>=1; --i)
if (ST.R[i].key==key) return i; //ST.R[i].key就是i元素的Key值
return 0;
}
当然这个算法有很多其他形式,这里给出一种:
int Search_Seq(SSTable ST,KeyType key){
for (i = ST.length; ST.R[i].key != key; --i); //注意后面有分号
if (i <= 0) break;
if (i > 0) return i;
else return 0;
}
上述算法的每一个元素都要判断两次:一是i是否大于1,二是元素是否相等。我们可否简化一下比较步骤?我们把待查关键字key存入表头(“哨兵”、”监视哨”),从后往前逐个比较,可免去查找过程中每一步都要检测是否查找完毕,加快速度。这样,若表中不存在,则返回结果自然是0,就取消了检查越界的操作。

int Search_Seq(SSTable ST,KeyType key){
ST.R[0].key = key;
for (i = ST.length; ST.R[i].key != key; --i); //注意后面有分号
return i;
}
下面分析顺序查找法的时间效率。比较次数与key位置有关:查找第i个元素,需要比较n-i+1次;查找失败,需比较n+1次。所以,算法的时间复杂度是O(n),查找成功时的平均查找长度是:
空间复杂度:一个辅助空间O(1);
讨论:(1)记录的查找概率不相等时如何提高查找效率?
查找表存储记录原则——按查找概率高低存储:查找概率越高,比较次数越少;查找概率越低,比较次数较多。
(2)记录的查找概率无法测定时如何提高查找效率?
方法——按查找概率动态调整记录顺序:
- 在每个记录中设一个访问频度域;
- 始终保持记录按非递增有序的次序排列;
- 每次查找后均将刚查到的记录直接移至表头。
(3)顺序查找法的优点:算法简单,逻辑次序无要求,且不同存储结构均适用。缺点:ASL太长,时间效率太低。
(2)折半查找(二分或对分查找)
特点:针对有序序列,每次将待查区间的长度缩小一半。
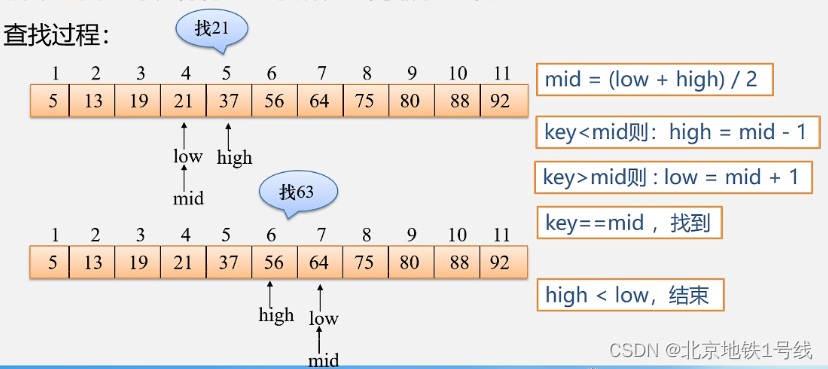
设表长为n,low、high和mid分别指向待查元素所在区间的上界、下界和中点,key为给定的要查找的值:
- 初始时,令low=1,high=n,mid=L(low+high)/2];
- 让k与mid指向的记录比较若key==R[mid].key,查找成功;若key<R[mid].key,则high=mid-1;若key>R[mid].key,则 low=mid+1;
- 重复上述操作,直至low>high时,查找失败;
int Search_Bin (SSTable ST,KeyType key){
low = 1;
high = ST.length; //置区间初值
while (low <= high){
mid = (low + high)/ 2;
if (ST.R[mid].key == key) return mid; //找到待查元素
else if (key < ST.R[mid].key) //缩小查找区间
high = mid - 1; //继续在前半区间进行查找
else
low = mid + 1; //继续在后半区间进行查找
}
return 0; //顺序表中不存在待查元素
} //Search_Bin
我们也可以用递归方法书写:
int Search_Bin(SSTable ST, keyType key, int low, int high){
if(low > high) return 0; //查找不到时返回0
mid = (low+high)/2;
if(key == ST.elem[mid].key)
return mid;
else if(key<ST.elem[mid].key)
Search_Bin(ST, key, low, mid-1); //递归,在前半区间进行查找
else
Search_Bin(ST, key, mid+1, high); //递归,在后半区间进行查找
}
下面分析折半查找法的性能。分析每个位置需要查找几次,我们可以画出判定树:
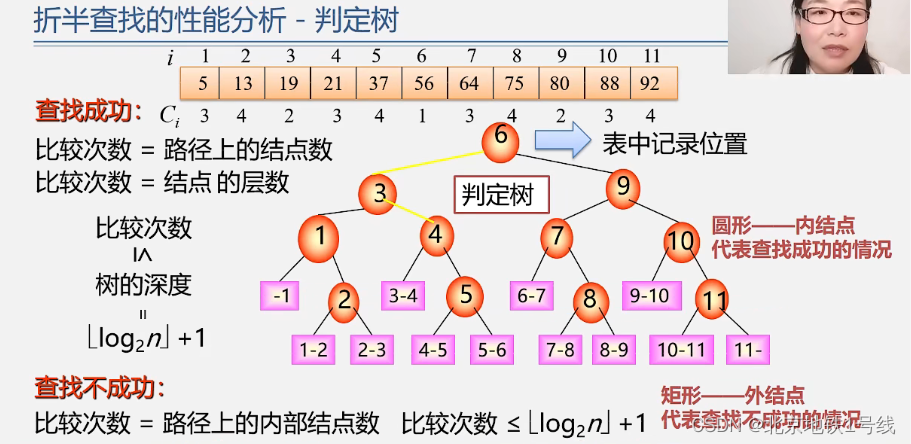
假设表长,则有
,此时判定树是高度为h的满二叉树。且假设表中每个元素查找的概率相等,
。不难得到:
折半查找优点:效率比顺序查找高。时间复杂度是O(lg n);
折半查找缺点:只适用于有序表,且限于顺序存储结构(对线性链表无效)。
(3)分块查找
举例:查字典,字典的编写把A-Z分成26块。分块查找的实质是索引顺序表上的查找。
方法:(1)将表分成几块,且分块有序(若i<j,则第j块中所有记录的关键字均大于第i块中的最大关键字),每块内的元素可以有序或无序;
(2)建立“索引表”(每个结点含有最大关键字域和指向本块第一个结点的指针,且按关键字有序)。
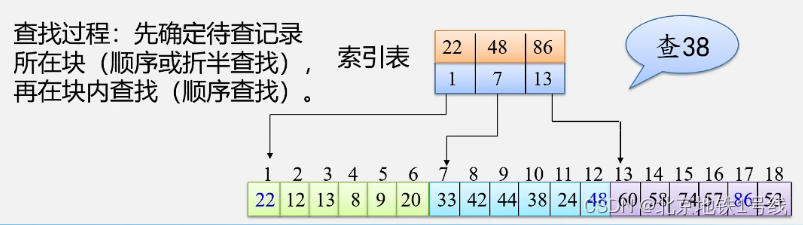
优点:插入和删除比较容易(本体链表,索引表顺序表),无需进行大量移动。
缺点:要增加一个索引表的存储空间并对初始索引表进行排序运算。
适用情况:如果线性表既要快速查找又经常动态变化,则可采用分块查找。