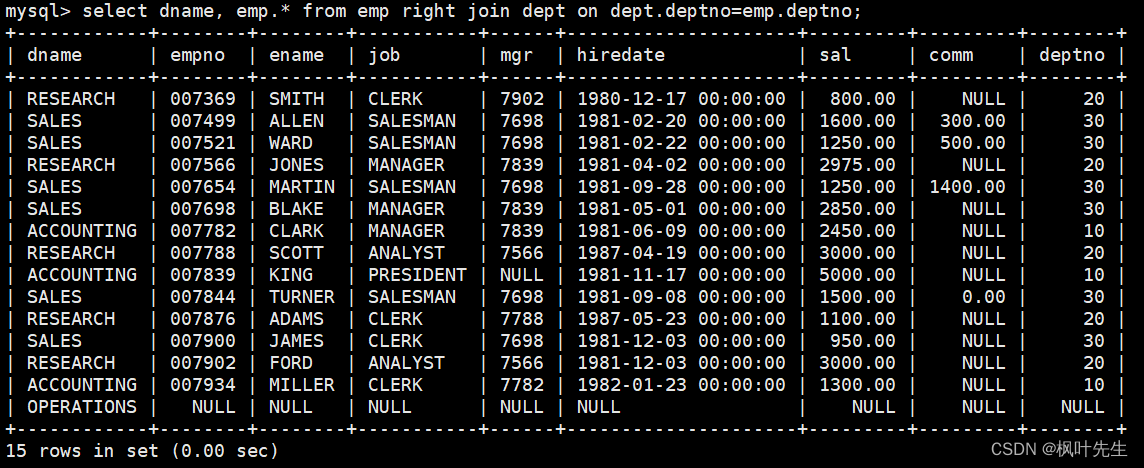
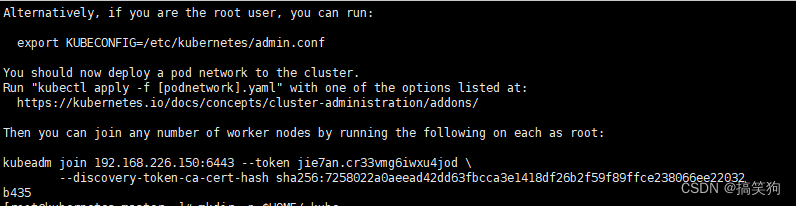
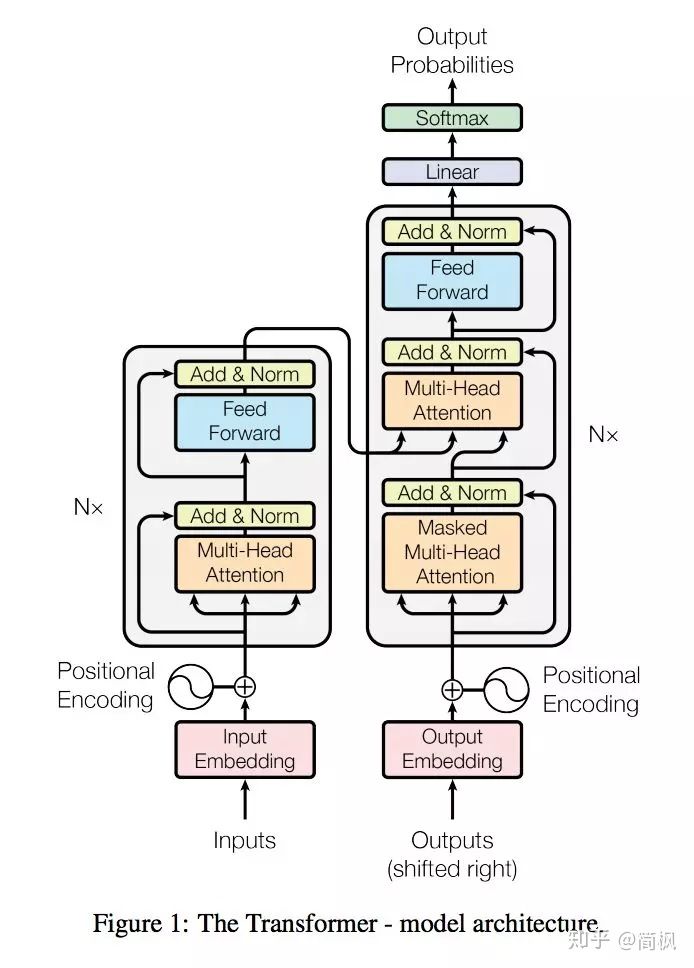
给你一根长度为 n 的绳子，请把绳子剪成整数长的 m 段（ m 、 n 都是整数， n > 1 并且 m > 1 ， m <= n ），每段绳子的长度记为 k[1],...,k[m] 。请问 k[1]*k[2]*...*k[m] 可能的最大乘积是多少？例如，当绳子的长度是 8 时，我们把它剪成长度分别为 2、3、3 的三段，此时得到的最大乘积是 18

思路一：动态规划

设计一个数组len[N]，用于存放长度为N的绳子裁剪后所能拥有的最大乘积。

如len[1]表示长度为1的绳子的最大值，len[2]表示长度为2的最大值。

由于长度为2只能剪一刀，故len[2]固定为1；

当len大于2时，则可以用两层循环，外层循环表示绳子的长度，里层循环用于表示本次所裁剪的绳子的长度，由于裁剪绳子长度不能超过当前绳子总长度，故内层结束条件为裁剪绳子长度等于绳子长度。所有裁剪结果中的最大值，就是当前长度绳的最大乘积。

具体实现：

   int cutRope(int n) {
        // write code here

        vector<int>dp(n+1,0);
      
        dp[2]=1;
        for(int i=3;i<=n;i++)
        {

         for(int j=2;j<i;j++)
         {
            dp[i]=max(dp[i],max(dp[i-j]*j,(i-j)*j));
         }

        }
        return dp[n];
    }

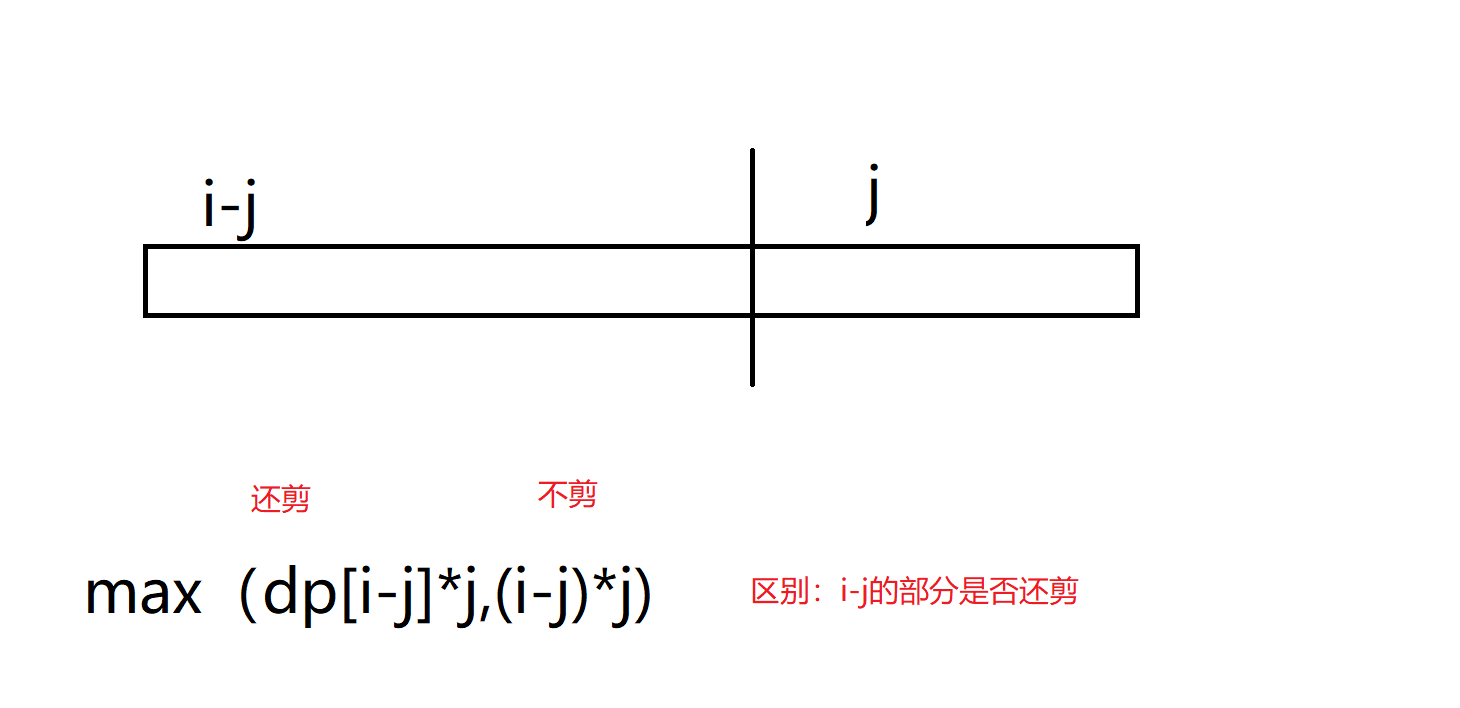
本题不好理解的点在“dp[i]=max(dp[i],max(dp[i-j]*j,(i-j)*j))”这一部分，其中max里的dp[i]表示剪2到j-1长度里的最大值，后面的max表示剪长度j的最大值，之所以再细分为两部分，是由于dp[i-j]*j默认对i-j部分又进行了裁剪，而（i-j）*j则表示未对该分部再进行裁剪。

 

思路二：数学分析

对于1到9的数字，1无法再分解，2分解后乘积最大为1，3分解后乘积最大为2，故2和3不分解的时候更大，对于4到9分解后最大情况如下：

4=2+2,  5=2+3，6=3+3， 7=3+2+2， 8=3+3+2， 9=3+3+3，可见对于任意一个数字，分解成一堆3和2时乘积最大，即拆分后的结果不能大于3，因为拆分后的数字大于3，则继续拆分可以乘积更大，而都可以拆分成3和2，为了使乘积结果更大，应该尽可能先拆3，最后再拆2.

具体代码如下：

int cutRope(int n) {
    // write code here
    if (n == 2)
    {
        return 1;
    }
    int mul = 1;
    if (n % 3 != 1)
    {
        while (n > 3)
        {
            mul *= 3;
            n -= 3;
        }
        mul *= n;
    }
    else {
        return 4 * pow(3, (n - 4) / 3);
    }
    return mul;

}

由于4拆分成2*2相比拆出3能得到更大的乘积，因此对于模3取余为1的数，拆3到最后一定会留下一个4，故可以先拆一个4，剩余的再拆3，故出现了if条件分支。