谷歌面试-扔鸡蛋

今天想跟大家分享一个有意思的面试题，这让我再一次感叹思维的奇妙，接下来我们一起看看吧~

首先来看看题目：

你有2颗鸡蛋，需要以最少的尝试次数来判断在100层的高楼上，哪一层楼是鸡蛋的安全层。

换句话说，就是需要确定我们从哪一层楼扔鸡蛋下去，鸡蛋恰好不会摔碎。高于安全层鸡蛋都会碎，低于安全层都不会碎。比如鸡蛋在第1层没有摔碎，在第2层摔碎了，那么鸡蛋的安全层就是第1层。

这里有几个假设条件：

没有摔碎的鸡蛋可以重复使用；
每颗鸡蛋的坚硬程度都是相同的。

在这里插入图片描述

这道题乍一看挺简单的，但其实解答相对复杂，而且解法多种多样，要在面试时逻辑清楚地表达完整思路，不仅要求面试者的知识储备要广、反应能力要快，逻辑思维和语言表达能力也是必不可少的。

成为经典可谓当之无愧。

解法1：简单粗暴

我们先来个最省事儿的方法：假设我们只有一颗鸡蛋，显然只有从一楼开始扔，逐层试探，直到鸡蛋摔碎，安全层就是第N-1层。

但是缺点想必大家也看出来了，这是拼运气啊，最坏情况需要扔100次。

用一颗鸡蛋的方法虽然简单粗暴，但也是给两颗鸡蛋的情况缕清一些思路。

简单写一下如何实现：

// 假设arr表示100层楼,每层楼鸡蛋会不会碎,如果arr[i] === 1 表示i层楼的鸡蛋会碎,arr[i] === 0表示第i层楼的鸡蛋不会碎

// 简单暴力
const throwEggs1 = (arr) => {
  for(let i = 1; i <= 100; i++) {
    if (arr[i] === 1) {
      return i
    }
  }
}

解法2：常规二分

有两颗鸡蛋，二分法想必是大多数同学脑海里浮现的第一个念头吧？

我们先从50楼扔一颗鸡蛋，如果没碎，就往上继续二分，到75楼继续扔······

这是比较顺利的情况，如果不顺利呢，比如我们从50楼扔鸡蛋，直接碎了，那就只有一颗鸡蛋了。

这时候我们就回到解法1了，只能从1楼开始遍历，又是拼运气的时候了，要是运气好，1楼鸡蛋就没了，那测试次数就是1+1=2次，但最坏情况就是1+49=50次。

这么多次，显然是不能通过google面试的。

// 常规二分

const throwEggs2 = (arr) => {
  let left = 1
  let right = 100
  let mid = 0
  while(left <= right) {
    mid = Math.floor(left + right) / 2
    if (arr[mid] === 0) {
      left = mid + 1
    } else {
      right = mid - 1
    }
  }
  return mid
}

解法3：均衡切割

虽然二分法不够优秀，但体现了切分范围的思想。

我们的基本思路是，将100层切分成两个维度，由两个鸡蛋分别控制一个维度。

一个维度是用第一颗鸡蛋分金定穴，另一个维度是用第二颗鸡蛋在前蛋的基础上进行遍历。

换言之，我们是将100层切分成若干个区块，由第一颗鸡蛋确定最高安全楼层所属的区块，再由第二颗鸡蛋逐层确定其具体的位置。

在1-100层楼之间，假设我们从上往下尝试，即从100层开始扔第一颗蛋，大概率是碎了，那第二颗蛋便又回到了解法1。

所以，我们应该从下往上进行划分、尝试，这样即使第一颗鸡蛋碎了，用第二颗蛋遍历的成本也比较低。

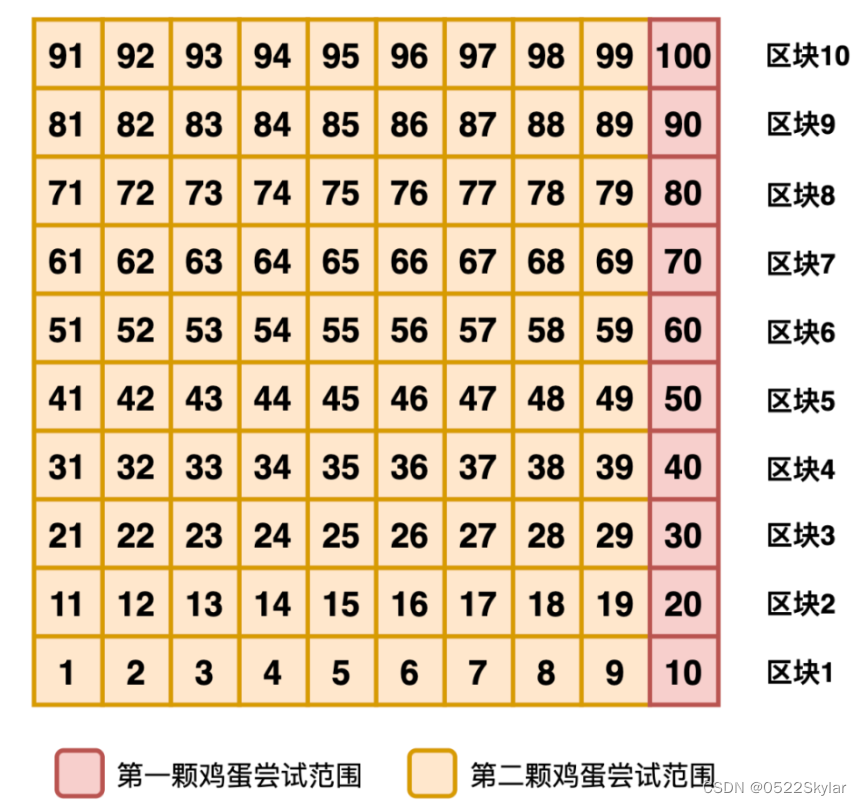
比如第一颗蛋每10层扔一次，第一次从10层扔，第二次从20层扔，第三次从30层扔……一直扔到100层。

第二颗蛋就只用在第一颗蛋摔碎的层数和前一次的安全层之间的9层进行范围遍历。

也就是说，要是第一颗鸡蛋在第30层摔碎了，那就拿第二颗蛋从21层到29层逐层尝试。

这样的最好情况就是第一颗蛋在第10层碎掉，总的尝试次数为1+1=2次。

最坏的情况是在第100层碎掉，总尝试次数为10+9=19次。

在这里插入图片描述

// 均衡切割
const throwEggs3 = (arr) => {
  let count = 0
  // 第一个鸡蛋
  for (let i = 1; i < 10; i++) {
    if (arr[i * 10] === 1) {
      count = i * 10
      break
    }
  }
  // 第二个鸡蛋
  for(let i = count - 1; i >= count - 10; i--) {
    if (arr[i] !== 1) {
      return i
    }
  }
}

解法4：微妙平衡

上面的方法，看似已经比较完美了。

但是我们再具像化一点，就能发现问题：第一颗鸡蛋能快速定位安全楼层低的情况，但如果安全楼层位置越高，耗时就会越久，而第二颗鸡蛋在每个区块内的消耗，都是一样的。

如果鸡蛋的最高安全层为18或者98，用解法3的思路的话，这两种情况的总尝试次数并不一样：

最高安全楼层为18时，第一颗鸡蛋试了2次就定位了区块；而最高安全楼层为98时，第一颗鸡蛋试了10次才定位了区块。

虽然第二颗鸡蛋在区块内部的逐层尝试次数是一样的，但98层对应的总尝试次数就多太多了。

原因就是区块完全均匀划分对大数不利。

明白了这个缺陷，也就知道了改进的基本思想：要对100找出一种二维区块划分，但不是均匀划分。

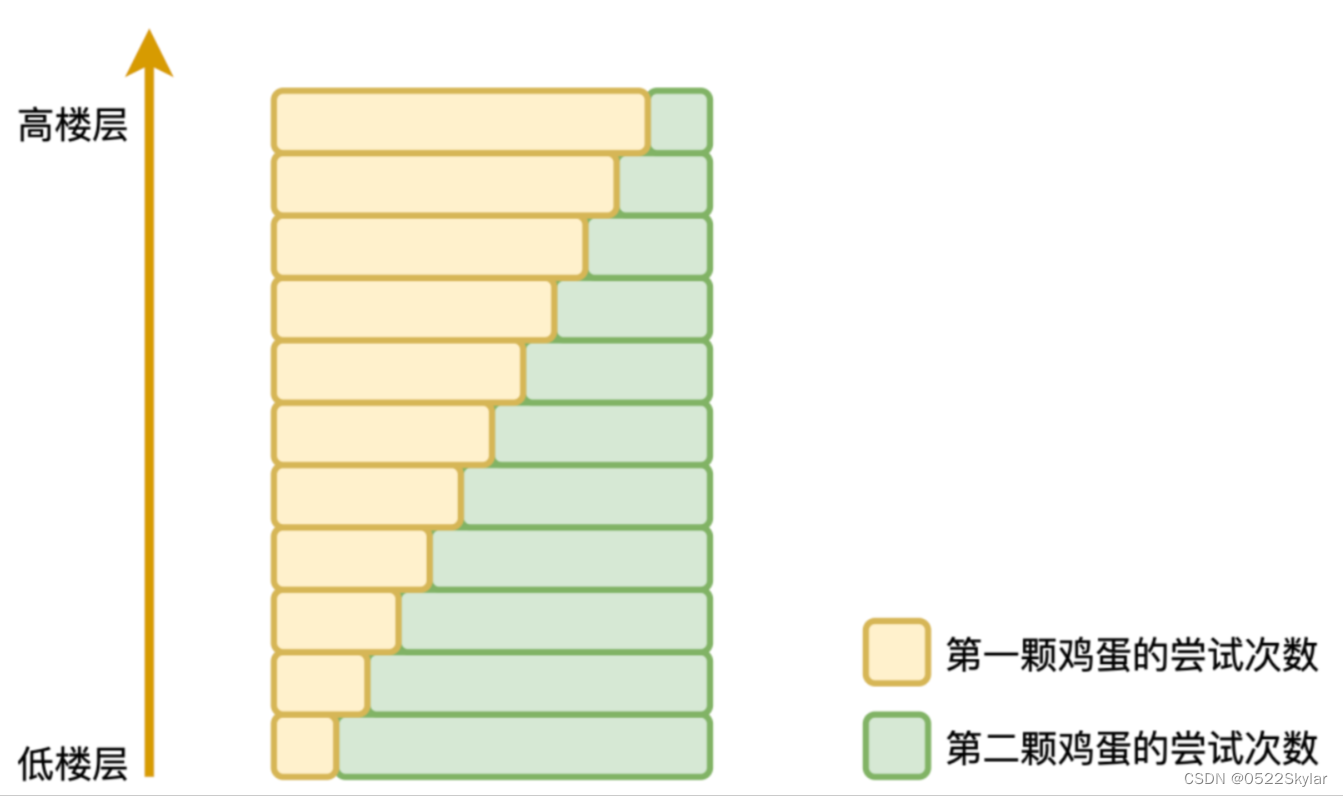
对于比较小的区块部分，其包含的楼层范围可以适当增加；越向大数部分走，其包含的楼层范围越来越小。从下往上，每一个区块内所含楼层递减。

在最高安全楼层比较低的情况下，第一颗鸡蛋尝试的次数少；在最高安全楼层比较高的情况下，则第二颗鸡蛋尝试的次数少。

就是用第二颗鸡蛋尝试次数的减少来弥补第一颗鸡蛋需要的尝试次数的递增，使两颗鸡蛋在不同维度上的尝试次数此消彼长，达到一种总体上的平衡。

每上一个区块，第一颗鸡蛋消耗的次数就+1，我们索性就假设每个区块包含的楼层数逐级递减1，以达到平衡。

那么每个区块包含的层数应该如何划分呢？

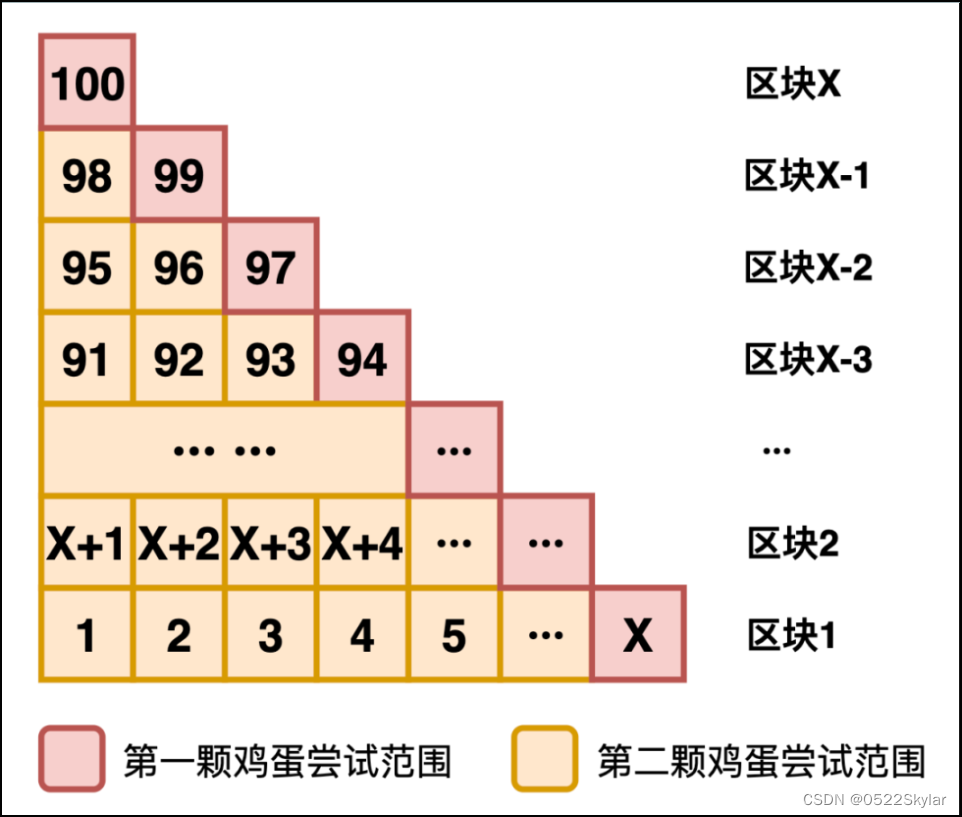
我们假设第一个区块有X层，那么第二个就是X-1，以此类推，我们就得到了一个方程式：

X+（X-1）+（X-2）+···+3+2+1≥100

可以看出来，这时候区块个数和第一个区块包含的层数其实是相等的。

在这里插入图片描述

现在我们回过头来，再仔细看看方程式，是不是有点熟悉，不就是等差数列求和么！

所以我们化简方程式：

X(X+1)/2≥100

这里X最小值我们向上取整，得到14。

有同学会问为什么一定到1呢，最后一个区块一定只有1层吗？

不是的，到1是表示在X个区块的情况下，最多能覆盖的层数。

比如我们这个例子，X是14，求出的楼层总数是105，也就是可以覆盖105层，题目要求的100层当然绰绰有余。

由此，第一个区块包含14层楼，即1到14层；

第二个区块包含13层楼，即15到27层；

第三个区块包含12层楼，即28到39层；

······

第一颗鸡蛋依次试第14、27、39、50、60、69、77、84、90、95、99、100层。只要期间任何一次鸡蛋碎了，就拿第二颗鸡蛋从上一次的安全层之后开始逐层尝试，直至第二颗鸡蛋也摔碎为止。

用这个方法，总次数一定不会超过14次。

因为最高安全楼层越高，第一颗鸡蛋的尝试次数也就越多，但第二颗鸡蛋的尝试次数随之越来越少，两者始终维持着一种微妙的平衡，最后总的尝试次数波动也不会太大。

在这里插入图片描述

下面是全部的代码实现：

// 假设arr表示100层楼,每层楼鸡蛋会不会碎,如果arr[i] === 1 表示i层楼的鸡蛋会碎,arr[i] === 0表示第i层楼的鸡蛋不会碎

// 暴力
const throwEggs1 = (arr) => {
  for(let i = 1; i <= 100; i++) {
    if (arr[i] === 1) {
      return i
    }
  }
}

// 常规二分

const throwEggs2 = (arr) => {
  let left = 1
  let right = 100
  let mid = 0
  while(left <= right) {
    mid = Math.floor(left + right) / 2
    if (arr[mid] === 0) {
      left = mid + 1
    } else {
      right = mid - 1
    }
  }
  return mid
}

// 均衡切割
const throwEggs3 = (arr) => {
  let count = 0
  // 第一个鸡蛋
  for (let i = 1; i < 10; i++) {
    if (arr[i * 10] === 1) {
      count = i * 10
      break
    }
  }
  // 第二个鸡蛋
  for(let i = count - 1; i >= count - 10; i--) {
    if (arr[i] !== 1) {
      return i
    }
  }
}

// 微妙平衡
const throwEggs4 = (arr) => {
  let block = 10
  let count = 0
  // block(block + 1) / 2 >= 100
  while(block * block + block < 100 * 2) {
    block++
  }
  // 第一个鸡蛋的尝试
  let temp = block // 每层区块的最后一个
  while(temp <= 100) {
    if (arr[temp] === 1) {
      count = temp
      break
    }
    --block
    temp += block
  }

  // 第二个鸡蛋的尝试
  for(let i = count - 1; i >= count - block; i--) {
    if (arr[i] === 0) {
      return i
    }
  }
}