1 KD树的问题
算法笔记:KD树_UQI-LIUWJ的博客-CSDN博客
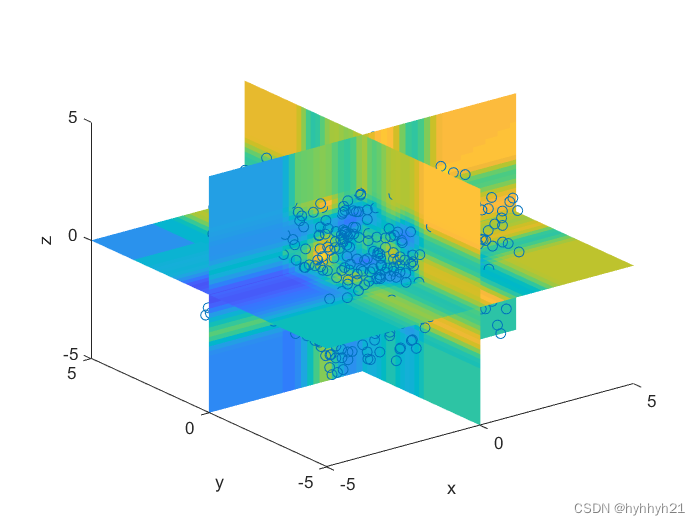
- 在kd树中,导致性能下降的最核心因素是因为kd-tree中被分割的子空间是一个个的超方体,而求最近邻时使用的是欧式距离(超球)。
- 超方体与超球体相交的可能性是极高的
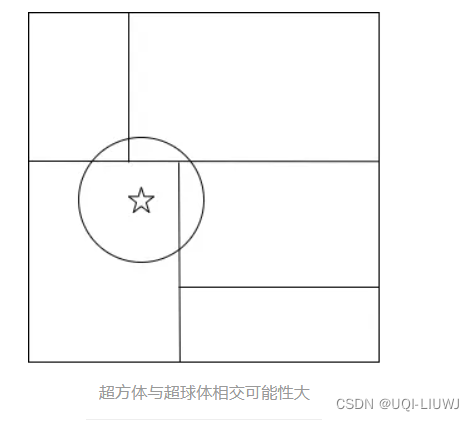
- 如上图所示,凡是相交的子空间,都需要进行检查,大大的降低运行效率
2 球树
- 如果划分区域也是超球体,则相交的概率大大降低
- ——>ball-tree通过超球体划分空间,去掉棱角,划分超球体和搜索超球体相交的概率大大降低
- 特别在数据维度很高时,算法效率得到大大提升
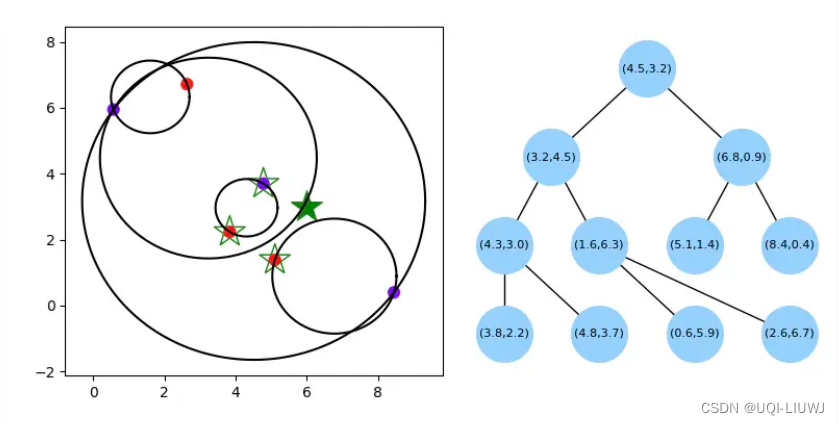
3 构建球树
def fit_ball_tree:
input: x, 数据点
output: node,构造好的ball tree的根节点
if 只有一个数据点:
创建一个叶子结点node包含这一单一的点:
node.pivot = x[0]
node.son1 = None
node.son2 = None
node.radius = 0 #球树半径
return node
else:
让c为最宽的维度
让p1,p2为该维度最两端的点
让p为这个维度的中心点 = (p1+p2)/2
让radius为p到x上最远点的距离
让xl为左集合(距离p1更近的所有点)
让xr为右集合(距离p2更近的所有点)
创建带有两个孩子的node:
node.pivot = p
node.label = None
node.son1 = fit_balltree(xl)
node.son2 = fit_balltree(xr)
node.radius = radius
return node
4 球树K近邻搜索
def ball_tree_search:
global:
Q, 缓存k个最近邻点(初始时包含一个无穷远点)
q, 与Q对应,保存Q中各点与测试点的距离
input:
k, 寻找k个最近邻
t, 测试点
node, 当前节点
output:
无
三角不等式:若测试点到当前球的最近距离大于到Q中最远点的距离,则当前球中不可能包含待搜索的近邻点
if distance(t, node.pivot) - node.radius ≥ max(q):
return
if node为叶节点:
将node.pivot添加到Q,并同步更新q
若Q内超过k个近邻点,则移出与测试点距离最远的那个点,并同步更新q
else:
递归搜索当前节点的左儿子和右儿子
ball_tree_search(k,t,node.son1)
ball_tree_search(k,t,node.son2)
参考内容:KNN的核心算法kd-tree和ball-tree - 简书 (jianshu.com)