如何在地图上寻找最密集点的位置？

news2024/9/9 7:43:28

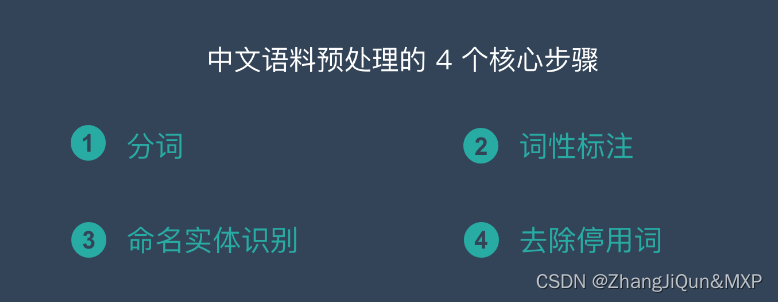
最近我在工作中遇到了一个小的需求点，大概是需要在地图上展示出一堆点中的点密度最密集的位置。最开始没想到好的方法，就使用了一个非常简单的策略——所有点的坐标求平均值，这个方法大部分的时候好用，因为大部分城市所有点位基本上都是围绕某个中心点向四周发散的。但我们实际在线上使用的时候，遇到了两个特殊的case。

首先就是当点位分布呈现出异形，比如哑铃型数据分布在两头，你们求平均值的方法就会找到中间数据密度最稀疏的地方，就比如我们在成都的数据上遇到的一样，下图中的红色点位就是按平均值求出来的中心点。
在这里插入图片描述
另外一种异常case就是数据呈现圆周分布的时候，比如北京的数据，北京的中心是故宫，我们不可能会有点位，如果直接求平均值的话，计算出来的中心点就在故宫附近，这里的数据反而是最稀疏的，如下图所示。
在这里插入图片描述
后来查询资料，了解到核密度这一方法可以解决我们所遇到的问题，经过实验后发现效果还不错，所以在这里分享给大家。核密度的思路也很简单，就是遍历所有的点位，计算其他点到当前点的核密度总值，然后找出平均密度最大的点。举个简单例子，给定一个点，如果其他某个点距这个点距离近，密度值就高，反之就远，这个点到其他所有点的密度和求平均就是这个点最终的密度值，这里我们可以直接选用距离的倒数来当成核函数，不过这个核函数是线性的，最终结果和我求平均值差异不大。

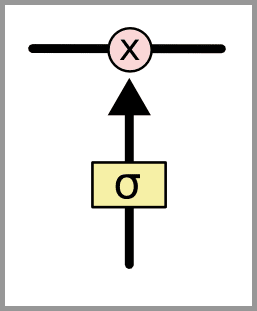
优化下思路，如果某个点的距离越远，是不是其带来的密度值应该越小？前人也是这么想的，于是就有了很多非线性核函数，而我最终使用了高斯核，调整好核函数的带宽后，其他点带来的密度值也会随着距离，以正态分布的方式衰减如下图，举例越远纵轴的坐标值越低，图中的sigma就是我们核函数的里的带宽。
在这里插入图片描述
接下来看下计算过程和效果，由于我们是Java系统，我的最终实现是用了java调用了simle包，整体代码如下：

	private double[] getHotpot(double[][] data) {
		// 创建高斯核
		MercerKernel<double[]> kernel = new GaussianKernel(0.02);

		// 计算所有点的核密度估计
		double[] densities = new double[data.length];
		for (int i = 0; i < data.length; i++) {
			for (int j = 0; j < data.length; j++) {
				densities[i] += kernel.k(data[i], data[j]);
			}
			// 计算平均密度
			densities[i] /= data.length;
		}

		// 找出密度最大的点
		int maxDensityIndex = 0;
		for (int i = 1; i < densities.length; i++) {
			if (densities[i] > densities[maxDensityIndex]) {
				maxDensityIndex = i;
			}
		}
		return data[maxDensityIndex];
	}

这里我带宽(高斯核中的sigma)用了0.02，这个也是多次调试后的结果，如果过大会导致算出来的密度值更接近于全局平均值，过小的话会出现几个点集中在一起，但周围没有其他点的情况，我们还是拿上面两个异常的case看下核密度方法的效果。首先就是成都哑铃型的数据。
在这里插入图片描述
再来就是北京的环形数据

上面的图中，我使用了python中的sklearn来实现核密度，使用了folium来绘制地图，完整的代码也贴出来供大家参考。

# -*- coding: utf-8 -*-
import folium
import pandas as pd
from sklearn.neighbors import KernelDensity
import numpy as np

def getCenterPoint(sites):
    points = sites[['latitude', 'longitude']].values
    weights = sites['score'].values
    
    # 实例化KernelDensity对象
    kde = KernelDensity(kernel='gaussian', bandwidth=0.02)

    # 对数据进行拟合
    kde.fit(points) 

    # 使用KDE模型评估每个点的密度
    log_densities = kde.score_samples(points)

    # 密度最高的点是评估密度最高（即，log_densities值最大）的点
    highest_density_point = points[np.argmax(log_densities)]

    print(highest_density_point.tolist())
    return highest_density_point.tolist()

# 创建一个以给定经纬度为中心的地图，初始缩放级别设为14
m = folium.Map(zoom_start=14)

for i, s in data.iterrows():
    # 在地图上添加一个点标记
    folium.Marker(
        location=[s['latitude'], s['longitude']],  # 经纬度
        popup=s['resblock'], 
    ).add_to(m)
# 保存为html文件
centerPoint = getCenterPoint(cityDf)
folium.Marker(
    location=centerPoint,  # 经纬度
    popup='中心点',  # 弹出内容
    radius=50,
    icon=folium.Icon(color="red", icon="info-sign")
).add_to(m)

m.location = centerPoint

m.save('map.html')