基于MATLAB的径向基函数插值（RBF插值）（一维、二维、三维）
- 0 前言
- 1 RBF思路
- 2 1维RBF函数
- 2.1 参数说明
- 2.1.1 核函数选择
- 2.1.2 作用半径
- 2.1.3 多项式拟合
- 2.1.4 误差项（光滑项）
- 3 2维RBF函数
- 4 3维RBF函数
惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。
0 前言
插值是一个工程中非常常见的扩展数据方法。通常数据测量数量永远是已知的，数据的储存空间也是有限的，但工程中的数据需求却永远是无限的。
如何用较少位置处的数据点来推广到任意位置处的数据点，是工程中常见的问题。其中径向基函数RBF插值具有不依赖数据网格的特点，省去了传统插值的网格剖分，是一种基于拟合的插值。
本文主要注重于具有几何意义上的RBF插值，所以只列举了一维二维和三维插值，更高维插值数据可以稍加改写代码就可以实现，本文也不再涉及。
本文的参考文献如下：
[1]Meshfree Approximation Methods with MATLAB.Gregory E. Fasshauer.
1 RBF思路
径向基函数的大概原理是利用一系列函数叠加，对原函数进行拟合。也就是:
F
(
x
)
=
∑
w
i
∗
f
i
(
x
0
,
x
)
F(x)=\sum w_i*f_i(x_0,x)
F(x)=∑wi∗fi(x0,x)
其中f(x0,x)为基函数，是中心对称函数，函数中心点在x0上。w为每个函数的权重。
因此，只需要求出权重w，就可以利用基函数在各个点的值，计算出整个域的函数。而求解权重，也是一个简单的线性代数问题，直接用线性方程组求逆的方式就可以得到。
因此，RBF方法也具有原理简单，编程容易的特点。
下面用一个简单的例子来解释。
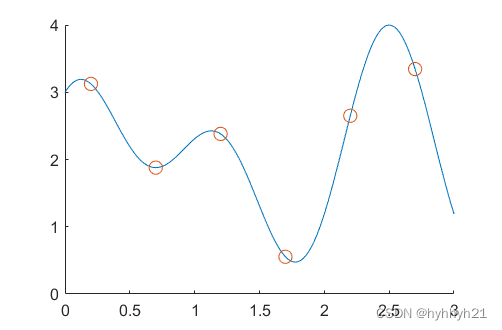
首先问题假设如下，我有下面6个点的数据（xi,yi），想插值出蓝色的曲线结果，该如何处理？
那么第一步，我们构造核函数。这里选用高斯函数作为核函数：
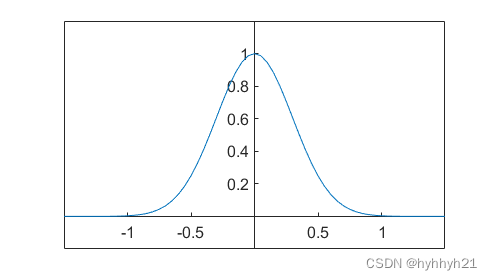
总共构造6个核函数f(x,xi)，每个核函数中心点在xi上。
f
i
(
x
)
=
e
x
p
(
−
(
x
−
x
i
)
2
/
2
/
s
2
)
f_i(x)=exp(-(x-x_i)^2/2/s^2)
fi(x)=exp(−(x−xi)2/2/s2)
每个函数乘以权重，可以得到当前基函数对应各个点的数值。以第一个基函数为例：
w
1
∗
[
f
1
(
x
1
)
f
1
(
x
2
)
f
1
(
x
3
)
f
1
(
x
4
)
f
1
(
x
5
)
f
1
(
x
6
)
]
w_1* \begin{bmatrix} f_1(x_1)\\ f_1(x_2)\\ f_1(x_3)\\ f_1(x_4)\\ f_1(x_5)\\ f_1(x_6)\\ \end{bmatrix}
w1∗
f1(x1)f1(x2)f1(x3)f1(x4)f1(x5)f1(x6)
则原函数F(x)可以计算为：
F
(
x
)
=
∑
w
i
∗
f
i
(
x
)
F(x)=\sum w_i*f_i(x)
F(x)=∑wi∗fi(x)
=
∑
w
i
∗
[
f
i
(
x
1
)
f
i
(
x
2
)
f
i
(
x
3
)
f
i
(
x
4
)
f
i
(
x
5
)
f
i
(
x
6
)
]
=\sum w_i*\begin{bmatrix} f_i(x_1)\\ f_i(x_2)\\ f_i(x_3)\\ f_i(x_4)\\ f_i(x_5)\\ f_i(x_6)\\ \end{bmatrix}
=∑wi∗
fi(x1)fi(x2)fi(x3)fi(x4)fi(x5)fi(x6)
=
[
f
1
(
x
1
)
f
2
(
x
1
)
f
3
(
x
1
)
f
4
(
x
1
)
f
5
(
x
1
)
f
6
(
x
1
)
f
1
(
x
2
)
f
2
(
x
2
)
f
3
(
x
2
)
f
4
(
x
2
)
f
5
(
x
2
)
f
6
(
x
2
)
f
1
(
x
3
)
f
2
(
x
3
)
f
3
(
x
3
)
f
4
(
x
3
)
f
5
(
x
3
)
f
6
(
x
3
)
f
1
(
x
4
)
f
2
(
x
4
)
f
3
(
x
4
)
f
4
(
x
4
)
f
5
(
x
4
)
f
6
(
x
4
)
f
1
(
x
5
)
f
2
(
x
5
)
f
3
(
x
5
)
f
4
(
x
5
)
f
5
(
x
5
)
f
6
(
x
5
)
f
1
(
x
6
)
f
2
(
x
6
)
f
3
(
x
6
)
f
4
(
x
6
)
f
5
(
x
6
)
f
6
(
x
6
)
]
∗
[
w
1
w
2
w
3
w
4
w
5
w
6
]
= \begin{bmatrix} f_1(x_1)&f_2(x_1)&f_3(x_1)&f_4(x_1)&f_5(x_1)&f_6(x_1)\\ f_1(x_2)&f_2(x_2)&f_3(x_2)&f_4(x_2)&f_5(x_2)&f_6(x_2)\\ f_1(x_3)&f_2(x_3)&f_3(x_3)&f_4(x_3)&f_5(x_3)&f_6(x_3)\\ f_1(x_4)&f_2(x_4)&f_3(x_4)&f_4(x_4)&f_5(x_4)&f_6(x_4)\\ f_1(x_5)&f_2(x_5)&f_3(x_5)&f_4(x_5)&f_5(x_5)&f_6(x_5)\\ f_1(x_6)&f_2(x_6)&f_3(x_6)&f_4(x_6)&f_5(x_6)&f_6(x_6)\\ \end{bmatrix}* \begin{bmatrix} w_1\\ w_2\\ w_3\\ w_4\\ w_5\\ w_6\\ \end{bmatrix}
=
f1(x1)f1(x2)f1(x3)f1(x4)f1(x5)f1(x6)f2(x1)f2(x2)f2(x3)f2(x4)f2(x5)f2(x6)f3(x1)f3(x2)f3(x3)f3(x4)f3(x5)f3(x6)f4(x1)f4(x2)f4(x3)f4(x4)f4(x5)f4(x6)f5(x1)f5(x2)f5(x3)f5(x4)f5(x5)f5(x6)f6(x1)f6(x2)f6(x3)f6(x4)f6(x5)f6(x6)
∗
w1w2w3w4w5w6
然后利用线性代数方式，就可以得到系数w。
则原函数F可以利用这些个基函数叠加得到：
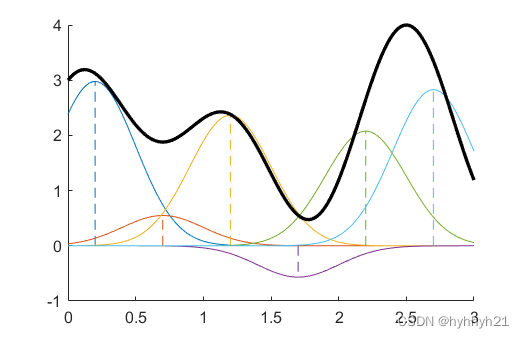
叠加后的函数和原函数对比见下图：
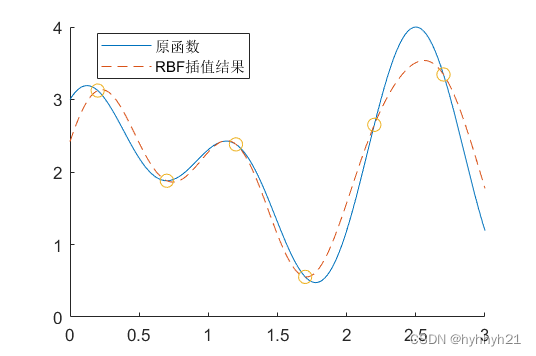可以看到计算结果还可以，曲线过渡也比较光滑。
如果已知的插值点更多，还可以拟合的更好。下图为10个已知点进行插值的结果，和预想曲线几乎重合。
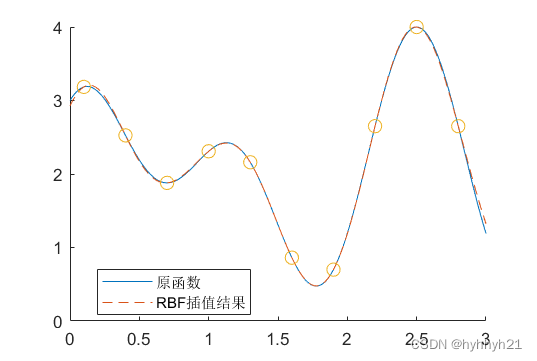
上面代码如下：
%RBF基本原理
clear
clc
close all
%插值点
x0=0.2:0.5:3;
y0=sin(2*pi*0.5*x0)+cos(2*pi*0.8*x0)+2;
%原函数
x2=0:0.02:3;
y2=sin(2*pi*0.5*x2)+cos(2*pi*0.8*x2)+2;
figure()
hold on
plot(x2,y2)
plot(x0,y0,'o','MarkerSize',8)
hold off
%1构造函数
N_k=length(x0);%构造函数的数量
RBF_Kernel=cell(N_k,1);
for k=1:N_k
x_k=x0(k);%中心位置，插值节点
RBF_Kernel_k=@(x) exp(-(x-x_k).^2/2/0.3^2);%正态函数
RBF_Kernel{k}=RBF_Kernel_k;%储存每个函数
end
%2计算出插值矩阵
InterpMat=zeros(N_k,N_k);
for k=1:N_k
RBF_phi_k=RBF_Kernel{k}(x0);%计算出当前正态函数
InterpMat(:,k)=RBF_phi_k(:);%插值矩阵每一列储存的都是对应的正态函数
end
%3利用插值矩阵求解出每个高斯函数的权重
%∑φ(k)*w(k)=InterpMat*w=y0，可以线性求逆直接得到系数w
w=InterpMat\y0';
%绘制出每个正态函数
figure()
hold on
mcp=colormap('lines');
for k=1:N_k
RBF_phi2_k=RBF_Kernel{k}(x2)*w(k);
plot(x2,RBF_phi2_k,'Color',mcp(k,:))
plot([x0(k),x0(k)],[0,RBF_Kernel{k}(x0(k))*w(k)],'Color',mcp(k,:),'LineStyle','--')
end
plot(x2,y2,'Color','k','LineWidth',2)
hold off
%绘制出最终相加的结果
y_RBF=zeros(size(y2));
for k=1:N_k
y_RBF=y_RBF+RBF_Kernel{k}(x2)*w(k);%叠加每一个正态函数
end
figure()
hold on
plot(x2,y2)
plot(x2,y_RBF,'--')
plot(x0,y0,'o','MarkerSize',8)
legend({'原函数','RBF插值结果'},'Location','best')
2 1维RBF函数
下面为1维RBF函数插值的代码，基本思路和上面第一章节的一样。但是对于计算速度和输入输出等方面简单做了一些优化。
计算结果如下：
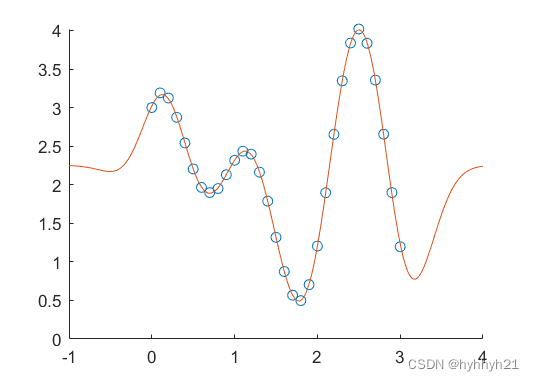
代码如下：
clear
clc
close all
%初始已知点
x0=0:0.1:3;
y0=sin(2*pi*0.5*x0)+cos(2*pi*0.8*x0)+2+0.02*rand(size(x0));
x=(-1:0.01:4);
y=RBF1(x0,y0,x,'gaussian',0.3,0,0.001);
figure()
hold on
plot(x0,y0,'o')
plot(x,y)
hold off
function y=RBF1(x0,y0,x,Method,Rs,Npoly,Error)
%一维RBF插值，输入x0散点，y0值。x是输出插值得到的点。
%Method方法，默认'linear'。
%'linear',|R|
%'gaussian',exp(-(R/Rs)^2)
%'thin_plate',R^2*log(R)
%'linearEpsR',|R|。分段线性插值，要求s更大一些
%'cubic',|R^3|
%Rs，插值核作用半径。Rs对于'linear'，'cubic'，'thin_plate'无影响。Rs大概和点和点之间的距离差不多就行。
%Npoly多项式拟合。默认是1，只拟合1次项。
%Error误差。在(-∞,∞)区间。默认是0，无误差。表示可以在部分误差范围内去插值。
%Error一般在0~1之内。如果只是为了收敛，可以比较小，在0.1以内就可以有很好效果；如果想实现平滑，可适当增大，大于1。
%示例：x0=0:0.3:pi;y0=sin(2*x0)+0.2*x0;x=-1:0.01:4;y=RBF1(x0,y0,x,'linear',0.2,1,0.0);
%示例：x0=0:0.1:3;y0=0.25*x0.^2-0.5*x0+0.1*rand(size(x0));x=-1:0.01:4;y=RBF1(x0,y0,x,'gaussian',0.3,2,0.01);
N=length(x0);%点的数量，也是RBF核的数量
%整理为列向量
x0=x0(:);
y0=y0(:);
x=x(:);
%函数默认信息
if nargin<4 || isempty(Method)
Method='linear';%默认线性核函数
elseif nargin<5 || isempty(Rs)
Rs=1.1*(max(x0)-min(x0))/N;%假设空间均匀分布
elseif nargin<6 || isempty(Npoly)
Npoly=1;%默认拟合1次项
elseif nargin<7 || isempty(Error)
Error=0;%默认输入数据没有误差
end
%选择核函数
K_method=0;
switch Method
case 'linear'
K_method=1;
fun=@(RMat) Kernel_Linear(RMat,Rs);
case 'gaussian'
K_method=2;
fun=@(RMat) Kernel_Gaussian(RMat,Rs);
Error=-Error;%因为零点不是零，远点是0，所以这里误差为负
case 'thin_plate'
K_method=3;
fun=@(RMat) Kernel_Thin_plate(RMat,Rs);
case 'linearEpsR'
K_method=4;
fun=@(RMat) Kernel_LinearEpsR(RMat,Rs);
Error=-Error;%因为零点不是零，远点是0，所以这里误差为负
end
%将原始数据分离出多项式项Npoly
if Npoly==0
C=ones(N,1);%常数项
wC=mean(y0);
elseif Npoly==1
C=[ones(N,1),x0];%常数项+一次项
wC=C\y0;
elseif Npoly==2
C=[ones(N,1),x0,x0.^2];%常数项+一次项+二次项
wC=C\y0;
else
error('只支持Npoly=0,1,2')
end
yC=C*wC;%多项式项
y1=y0-yC;
%计算每个基函数在各个点的值
K2=zeros(N);%每一列对应一个函数
%计算距离矩阵
DisMat=squareform(pdist(x0));
K3=fun(DisMat);%每一个核函数的中心点在节点上
K3=K3-Error*eye(N);%把误差函数加入
w=K3\y1;%计算权重
%根据权重计算插值
y=zeros(size(x));
for k=1:N %计算每个核的贡献，然后叠加
R_k=abs(x-x0(k));
yt=w(k)*fun(R_k );
%plot(t,yt);
y=y+yt;
end
NOut=length(y);
%再还原回多项式项
if Npoly==0
C=ones(NOut,1);%常数项
elseif Npoly==1
C=[ones(NOut,1),x];%常数项+一次项
elseif Npoly==2
C=[ones(NOut,1),x,x.^2];%常数项+一次项+二次项
end
y=y+C*wC;%再加上多项式项
%检查结果
if max(abs(w))/max(abs(y1))>1e3
warning('结果未收敛，建议调整误差Error');
elseif (max(y)-min(y))>5*(max(y0)-min(y0))
warning('结果未收敛，建议增大区间Eps，或者调整误差Error');
end
end
function z=Kernel_Linear(R,s)
%R距离
z=abs(R);%线性函数
end
function z=Kernel_Gaussian(R,s)
%R距离
%s大概和采样点间距差不多就行，可以略大（更胖）
z=exp(-R.^2/2/s^2);%正态函数
end
function z=Kernel_Thin_plate(R,s)
%R距离
z=R.^2.*log(R);%thin_plate
end
function z=Kernel_LinearEpsR(R,s)
%R距离
%s大概和采样点间距差不多就行，可以略大（更胖）
s=2*s;%这里要更大
z=s-R;%线性函数
z(z<0)=0;
end
2.1 参数说明
下面说一下上面函数RBF1的后面各项参数结果：
y=RBF1(x0,y0,x,Method,Rs,Npoly,Error)
2.1.1 核函数选择
RBF函数的核函数有非常多种，比如高斯函数、线性函数、薄板函数等。
下面以分别选择高斯函数和线性函数作为核函数的RBF进行对比：
clear
clc
close all
%初始已知点
x0=0:0.1:3;
y0=sin(2*pi*0.5*x0)+cos(2*pi*0.8*x0)+2+0.02*rand(size(x0));
x=(-1:0.01:4);
y=RBF1(x0,y0,x,'gaussian',0.3,0,0.001);
figure()
hold on
plot(x0,y0,'o')
plot(x,y)
hold off
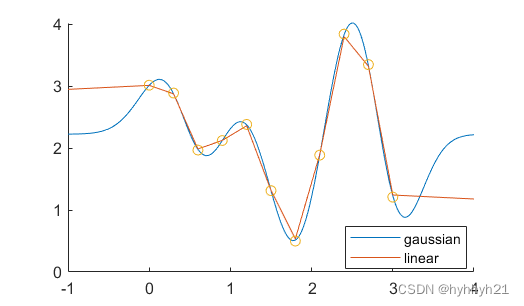
可以看到线性核函数的效果相当于线性插值，而高斯核函数对峰值的拟合预测很好，各有侧重点。
事实上，核函数的选择对RBF插值有重要影响，不同核函数对应着不同的场景。
2.1.2 作用半径
对于某些核函数，还需要确定其作用半径。比如对于高斯函数，半径越大，核越宽。
对于高斯函数，作用半径通常要大于两个散点之间距离，但最好不要太大。如果太小，会导致每个点都是一个孤立的峰。如果太大，会导致求系数时方程求解困难。
下面代码展示了作用半径为0.05、0.3和0.8半径的插值效果。
%初始节点
x0=0:0.3:3;
y0=sin(2*pi*0.5*x0)+cos(2*pi*0.8*x0)+2+0.02*rand(size(x0));
x=(-1:0.01:4);
y=RBF1(x0,y0,x,'gaussian',0.3,0,0.01);
y3=RBF1(x0,y0,x,'gaussian',0.05,0,0.0001);
y4=RBF1(x0,y0,x,'gaussian',0.8,0,0.0001);
figure()
hold on
plot(x,y3)
plot(x,y)
plot(x,y4)
plot(x0,y0,'o')
hold off
legend({'Rs=0.05','Rs=0.3','Rs=0.7'},'location','best')
ylim([-0.5,4.5])
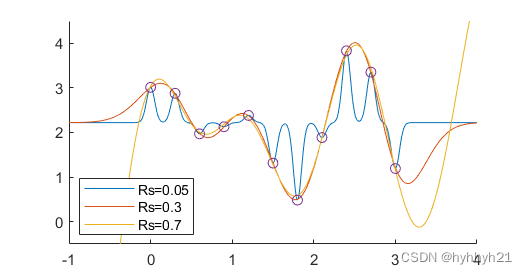
可以看到上面每个点的间距为0.2。当Rs很小的时候，每个点只有一个孤立的高斯峰。当Rs大于间距时，比如Rs=0.3和0.7，都可以求解出结果。
但当Rs比较大，比如Rs=0.7时，会出现计算很奇怪的解，比如系数w特别大。这种如果适当的加一小点误差Error（有一点就行，1e-3量级的已经足够了），放宽求解精度，可以避免这种系数w很大不收敛的情况。
2.1.3 多项式拟合
本RBF插值函数默认带一个常数项。因为像高斯函数等函数无穷大处是0，对于本身数值在0附近的函数插值效果还可以，但是函数距离x轴很远时，再用这些基函数去拟合效果就会非常差。
因此在RBF插值之前，需要先求出常数项C，然后将所有散点的yi减去这个常数项C。之后计算完系数再插值后，再把这个常数项C加上。
一次项也是同样的原理，就是先拟合出y’=kx+b，然后把所有散点yi-y’，得到计算系数用的y值。之后再把这个一次项加上即可。
通常常数项一般就够，除非数据有很明显的线性度。
下面代码展示了常数项和一次项对比插值的效果：
x0=0:0.3:3;
x=(-1:0.01:4);
y0=sin(2*pi*0.5*x0)+cos(2*pi*0.8*x0)+1+2*x0+0.02*rand(size(x0));
y1=RBF1(x0,y0,x,'gaussian',0.3,0,0.0001);
y2=RBF1(x0,y0,x,'gaussian',0.3,1,0.0001);
figure()
hold on
plot(x,y1)
plot(x,y2)
plot(x0,y0,'o')
hold off
legend({'常数项','一次项'},'location','best')
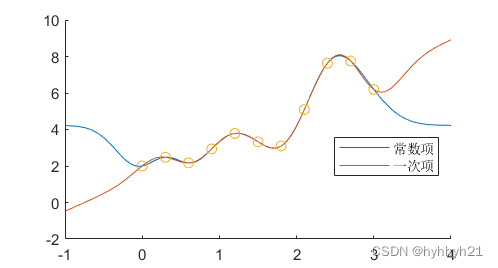
2.1.4 误差项（光滑项）
当数据采集具有一定的误差，或者计算不需要完全贴合每一个点的数据，或者拟合出的曲线太曲折需要光滑，或者计算出的系数w过大甚至不收敛，都可以适当的添加误差项来解决。
其中系数w不收敛的问题，可能是由于核半径Rs过大，或者原始数据本身不太好导致的。适当添加一点误差，1e-3甚至更小，就可以解决这个问题。
而如果想要消除误差，光滑曲线，则需要较大的数，比如0.2，甚至超过1。这个根据具体效果来看。
这个的原理是直接在矩阵K的对角线上减去一个数。这样可以略微放宽求解的约束，使得节点处的数值不一定是控制点数值。
下面展示了添加了随机项后，大误差和小误差项的对比代码和结果：
x0=0:0.1:3;
y0=sin(2*pi*0.5*x0)+cos(2*pi*0.8*x0)+1+0.4*randn(size(x0));
x=(-0.0:0.01:3.0);
y1=RBF1(x0,y0,x,'gaussian',0.15,0,0.0001);
y2=RBF1(x0,y0,x,'gaussian',0.15,0,0.3);
figure()
hold on
plot(x,y1)
plot(x,y2)
plot(x0,y0,'o')
hold off
legend({'小误差项','大误差项'},'location','best')
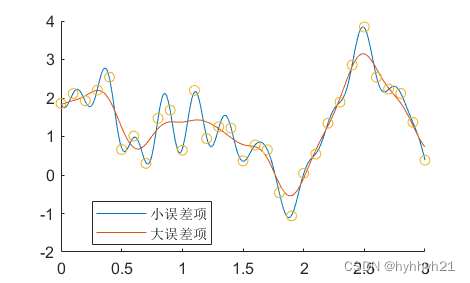
可以看到小误差项，曲线经过了每一个散点。大误差项，曲线只是大致经过了散点。
3 2维RBF函数
二维RBF函数的原理和一维相同。
z=RBF2(x0,y0,z0,x,y,Method,Rs,Npoly,ExtrapMethod,Error)
其中x0、y0是已知散点，z0是对应的值。然后要插值出x、y对应的值。
二维RBF函数额外考虑了外插的方法。通常并不建议数据外插，因为缺乏足够的信息。
本函数总共考虑了三种外插方法：
第一个是’rbf’，其实就是RBF方法算出来多少就是多少。
第二个是’nearest’，就是不外插，超出包线的点的数值直接等于相邻数据点数值。
第三个是’ploy’，是多项式外插，超出包线的点，按照多项式拟合的值计算得到，适用于波动不大的数据。
推荐’rbf’方法，因为不需要计算包线，如果不怎么考虑外插的话，非常节省时间。
下面展示了二维RBF插值计算的结果：
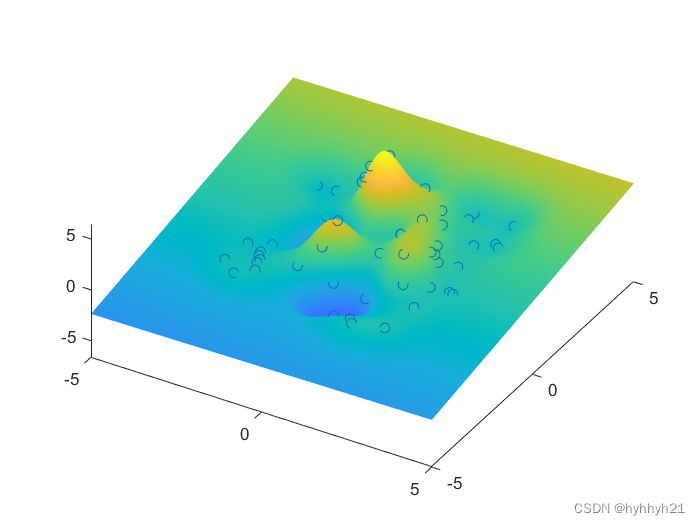
可以看到RBF插值可以较好的拟合出预期的效果。
展示的代码如下：
clear
clc
close all
%初始节点
N=60;
x0=rand(N,1)*6-3;%-3~3
y0=rand(N,1)*6-3;%-3~3
z0=peaks(x0,y0)+0.05*x0;
[x,y]=meshgrid(-5:0.02:5);
%二维RBF插值
z3=RBF2(x0,y0,z0,x,y,'gaussian',0.5,1,'rbf',0.001);
z=zeros(size(x));z(:)=z3(:);
figure()
hold on
surf(x,y,z,'EdgeColor','none');
scatter3(x0,y0,z0)
hold off
function z=RBF2(x0,y0,z0,x,y,Method,Rs,Npoly,ExtrapMethod,Error)
%二维RBF插值，输入x0，y0散点，z0值。x，y是输出插值得到的点。
%Method方法，默认'linear'。
%'linear',|R|
%'gaussian',exp(-(R/Rs)^2)
%'thin_plate',R^2*log(R)
%'linearEpsR',|R|。分段线性插值，要求s更大一些
%'cubic',|R^3|
%Rs，插值核作用半径。Rs对于'linear'，'cubic'，'thin_plate'无影响。Rs大概和点和点之间的距离差不多就行。
%Npoly多项式拟合。默认是1，只拟合1次项。
%ExtrapMethod,外插方法。某个数，全部赋值为这个数。'nearest'，按照临近值外插。'ploy'，多项式外插。'rbf'，默认用RBF插值得到的值。
%Error误差。在(-∞,∞)区间。默认是0，无误差。表示可以在部分误差范围内去插值。
%Error一般在0~1之内。如果只是为了收敛，可以比较小，在0.1以内就可以有很好效果；如果想实现平滑，可适当增大，大于1。
%示例：
N=numel(x0);%点的数量，也是RBF核的数量
%整理为列向量
x0=x0(:);
y0=y0(:);
z0=z0(:);
x=x(:);
y=y(:);
%计算包线
[k_ch,V]=convhull(x0,y0);
if V<=0
warning('输入散点过于集中');
end
%函数默认信息
narginchk(5,10)
if nargin<7 || isempty(Method)
Method='linear';%默认线性核函数
elseif nargin<8 || isempty(Rs)
Rs=1.1*(max(x0)-min(x0))/N;%假设空间均匀分布
elseif nargin<9 || isempty(Npoly)
Npoly=1;%默认拟合1次项
elseif nargin<10 || isempty(Npoly)
ExtrapMethod='rbf';%默认不外插
elseif nargin<11 || isempty(Error)
Error=0;%默认输入数据没有误差
end
%选择核函数
switch Method
case 'linear'
fun=@(RMat) Kernel_Linear(RMat,Rs);
case 'gaussian'
fun=@(RMat) Kernel_Gaussian(RMat,Rs);
Error=-Error;%因为零点不是零，远点是0，所以这里误差为负
case 'thin_plate'
fun=@(RMat) Kernel_Thin_plate(RMat,Rs);
case 'linearEpsR'
fun=@(RMat) Kernel_LinearEpsR(RMat,Rs);
Error=-Error;%因为零点不是零，远点是0，所以这里误差为负
end
%将原始数据分离出多项式项Npoly
if Npoly==0
C=ones(N,1);%常数项
wC=mean(z0);
elseif Npoly==1
if N<2;warning('点数太少，建议Npoly等于0');end
C=[ones(N,1),x0,y0];%常数项+一次项
wC=C\z0;
elseif Npoly==2
if N<5;warning('点数太少，建议Npoly等于1');end
C=[ones(N,1),x0,y0,x0.^2,y0.^2,x0.*y0];%常数项+一次项+二次项
wC=C\z0;
else
error('只支持Npoly=0,1,2')
end
zC=C*wC;%多项式项
z1=z0-zC;
%计算距离矩阵
DisMat=squareform(pdist([x0,y0]));
K3=fun(DisMat);%每一个核函数的中心点在节点上
K3=K3-Error*eye(N);%把误差函数加入
w=K3\z1;%计算权重
%根据权重计算插值
z=zeros(size(x));
for k=1:N %计算每个核的贡献，然后叠加
R_k=sqrt((x-x0(k)).^2+(y-y0(k)).^2);
zt=w(k)*fun(R_k );
z=z+zt;
end
NOut=length(z);
%再还原回多项式项
if Npoly==0
C=ones(NOut,1);%常数项
elseif Npoly==1
C=[ones(NOut,1),x,y];%常数项+一次项
elseif Npoly==2
C=[ones(NOut,1),x,y,x.^2,y.^2,x.*y];%常数项+一次项+二次项
end
zC2=C*wC;%再加上多项式项
%判断外插方法
Inpoly=inpolygon(x,y,x0(k_ch),y0(k_ch));%多边形内
indxInpoly=find(Inpoly);
if isnumeric(ExtrapMethod)
z(Inpoly)=z(Inpoly)+zC1(Inpoly);%内部的正常
z(~Inpoly)=ExtrapMethod;%外部的固定值
elseif ischar(ExtrapMethod)
switch ExtrapMethod
case 'rbf'
z=z+zC2;%再加上多项式项
case 'ploy'
z(Inpoly)=z(Inpoly)+zC2(Inpoly);%内部的正常
z(~Inpoly)=zC2(~Inpoly);%外部的直接用多项式值
case 'nearest'
z(Inpoly)=z(Inpoly)+zC2(Inpoly);%内部的正常
%找到最近的点
F = scatteredInterpolant(x(Inpoly),y(Inpoly),z(Inpoly),'nearest','nearest');
%外部的直接插值
z(~Inpoly)=F(x(~Inpoly),y(~Inpoly));
end
else
error('未识别ExtrapMethod')
end
%检查结果
if max(abs(w))/max(abs(z1))>1e3
warning('结果未收敛，建议调整误差Error');
elseif (max(z)-min(z))>5*(max(z0)-min(z0))
warning('结果未收敛，建议增大区间Eps，或者调整误差Error');
end
end
function z=Kernel_Linear(R,s)
%R距离
z=abs(R);%线性函数
end
function z=Kernel_Gaussian(R,s)
%R距离
%s大概和采样点间距差不多就行，可以略大（更胖）
z=exp(-R.^2/2/s^2);%正态函数
end
function z=Kernel_Thin_plate(R,s)
%R距离
z=R.^2.*log(R);%thin_plate
end
function z=Kernel_LinearEpsR(R,s)
%R距离
%s大概和采样点间距差不多就行，可以略大（更胖）
s=2*s;%这里要更大
z=s-R;%线性函数
z(z<0)=0;
end
4 3维RBF函数
计算方法和二维的方法一致。其实更高维的数据计算方法也相差不多。
对于实际工程的几何插值使用，最高维度也就是三维。对于其它应用可能还是需要高维的插值，本文暂不涉及，由于RBF代码较为简单，因此稍加改动即可更改为高维RBF插值结果。
三维RBF函数的原理和二维也相同。
P=RBF3(x0,y0,z0,P0,x,y,z,Method,Rs,Npoly,ExtrapMethod,Error)
其中x0、y0、z0是已知散点，P0是对应的值。然后要插值出x、y、z对应的值。
下面展示了三维RBF插值计算的结果和对应代码：
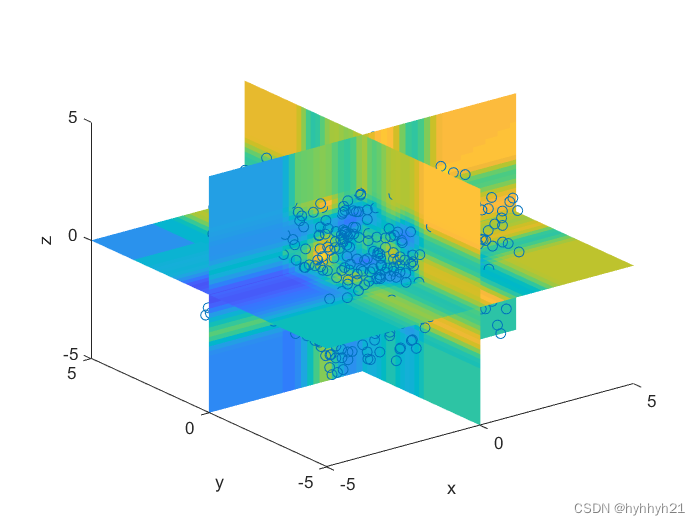
clear
clc
close all
%初始节点
N=1000;
x0=rand(N,1)*6-3;%-3~3
y0=rand(N,1)*6-3;%-3~3
z0=rand(N,1)*6-3;%-3~3
P0=sin(1*pi*x0)+cos(1.5*pi*y0)+sin(1*pi*z0)+1;
[x,y,z]=meshgrid(-5:0.2:5);
P3=RBF3(x0,y0,z0,P0,x,y,z,'linear',0.5,1,'nearest',0.01);%RBF插值
P=zeros(size(x));P(:)=P3(:);
%实际插值结果
figure()
hold on
s=slice(x,y,z,P,[0],[0],[0]);
set(s,'LineStyle','none');
scatter3(x0,y0,z0)
hold off
xlabel('x');ylabel('y');zlabel('z');
view(3)
%理论目标结果
figure()
P3=sin(1*pi*x)+cos(1.5*pi*y)+sin(1*pi*z)+1;
P3(x>3)=0;P3(y>3)=0;P3(z>3)=0;P3(x<-3)=0;P3(y<-3)=0;P3(z<-3)=0;
s=slice(x,y,z,P3,[0],[0],[0]);
xlabel('x');ylabel('y');zlabel('z');
view(3)
function P=RBF3(x0,y0,z0,P0,x,y,z,Method,Rs,Npoly,ExtrapMethod,Error)
%二维RBF插值，输入x0，y0散点，z0值。x，y是输出插值得到的点。
%Method方法，默认'linear'。
%'linear',|R|
%'gaussian',exp(-(R/Rs)^2)
%'thin_plate',R^2*log(R)
%'linearEpsR',|R|。分段线性插值，要求s更大一些
%'cubic',|R^3|
%Rs，插值核作用半径。Rs对于'linear'，'cubic'，'thin_plate'无影响。Rs大概和点和点之间的距离差不多就行。
%Npoly多项式拟合。默认是1，只拟合1次项。
%ExtrapMethod,外插方法。某个数，全部赋值为这个数。'nearest'，按照临近值外插。'rbf'，默认用RBF插值得到的值。三维外插判据复杂，不建议用。
%Error误差。在(-∞,∞)区间。默认是0，无误差。表示可以在部分误差范围内去插值。
%Error一般在0~1之内。如果只是为了收敛，可以比较小，在0.1以内就可以有很好效果；如果想实现平滑，可适当增大，大于1。
N=numel(x0);%点的数量，也是RBF核的数量
%整理为列向量
x0=x0(:);
y0=y0(:);
z0=z0(:);
P0=P0(:);
x=x(:);
y=y(:);
z=z(:);
%计算包线
[k_ch,V]=convhull(x0,y0,z0);
%函数默认信息
narginchk(7,12)
if nargin<7 || isempty(Method)
Method='linear';%默认线性核函数
elseif nargin<8 || isempty(Rs)
Rs=1.1*(max(x0)-min(x0))/N;%假设空间均匀分布
elseif nargin<9 || isempty(Npoly)
Npoly=1;%默认拟合1次项
elseif nargin<10 || isempty(Npoly)
ExtrapMethod='rbf';%默认不外插
elseif nargin<11 || isempty(Error)
Error=0;%默认输入数据没有误差
end
%选择外插包线
if strcmp(ExtrapMethod,'rbf')
Inpoly=[];
else
k_ch=unique(k_ch);
Inpoly=IsPointInShape3([x0(k_ch),y0(k_ch),z0(k_ch)],[x,y,z]);
end
if V<=0
warning('输入散点过于集中');
end
%选择核函数
switch Method
case 'linear'
fun=@(RMat) Kernel_Linear(RMat,Rs);
case 'gaussian'
fun=@(RMat) Kernel_Gaussian(RMat,Rs);
Error=-Error;%因为零点不是零，远点是0，所以这里误差为负
case 'thin_plate'
fun=@(RMat) Kernel_Thin_plate(RMat,Rs);
case 'linearEpsR'
fun=@(RMat) Kernel_LinearEpsR(RMat,Rs);
Error=-Error;%因为零点不是零，远点是0，所以这里误差为负
end
%将原始数据分离出多项式项Npoly
if Npoly==0
C=ones(N,1);%常数项
wC=mean(P0);
elseif Npoly==1
if N<3;warning('点数太少，建议Npoly等于0');end
C=[ones(N,1),x0,y0,z0];%常数项+一次项
wC=C\P0;
elseif Npoly==2
if N<9;warning('点数太少，建议Npoly等于1');end
C=[ones(N,1),x0,y0,z0,x0.^2,y0.^2,z0.^2,x0.*y0,x0.*z0,z0.*y0];%常数项+一次项+二次项
wC=C\P0;
else
error('只支持Npoly=0,1,2')
end
PC=C*wC;%多项式项
P1=P0-PC;
%计算距离矩阵
DisMat=squareform(pdist([x0,y0,z0]));
K3=fun(DisMat);%每一个核函数的中心点在节点上
K3=K3-Error*eye(N);%把误差函数加入
w=K3\P1;%计算权重
%根据权重计算插值
P=zeros(size(x));
for k=1:N %计算每个核的贡献，然后叠加
R_k=sqrt((x-x0(k)).^2+(y-y0(k)).^2+(z-z0(k)).^2);
Pt=w(k)*fun(R_k );
P=P+Pt;
end
NOut=length(P);
%再还原回多项式项
if Npoly==0
C=ones(NOut,1);%常数项
elseif Npoly==1
C=[ones(NOut,1),x,y,z];%常数项+一次项
elseif Npoly==2
C=[ones(NOut,1),x,y,z,x.^2,y.^2,z.^2,x.*y,x.*z,z.*y];%常数项+一次项+二次项
end
PC2=C*wC;%再加上多项式项
%判断外插方法
if isnumeric(ExtrapMethod)
P(Inpoly)=P(Inpoly)+zC1(Inpoly);%内部的正常
P(~Inpoly)=ExtrapMethod;%外部的固定值
elseif ischar(ExtrapMethod)
switch ExtrapMethod
case 'rbf'
P=P+PC2;%再加上多项式项
case 'ploy'
P(Inpoly)=P(Inpoly)+PC2(Inpoly);%内部的正常
P(~Inpoly)=PC2(~Inpoly);%外部的直接用多项式值
case 'nearest'
P(Inpoly)=P(Inpoly)+PC2(Inpoly);%内部的正常
%找到最近的点
F = scatteredInterpolant(x(Inpoly),y(Inpoly),z(Inpoly),P(Inpoly),'nearest','nearest');
%外部的直接插值
P(~Inpoly)=F(x(~Inpoly),y(~Inpoly),z(~Inpoly));
end
else
error('未识别ExtrapMethod')
end
%检查结果
if max(abs(w))/max(abs(P1))>1e3
warning('结果未收敛，建议调整误差Error');
elseif (max(P)-min(P))>5*(max(P0)-min(P0))
warning('结果未收敛，建议增大区间Eps，或者调整误差Error');
end
end
function z=Kernel_Linear(R,s)
%R距离
z=abs(R);%线性函数
end
function z=Kernel_Gaussian(R,s)
%R距离
%s大概和采样点间距差不多就行，可以略大（更胖）
z=exp(-R.^2/2/s^2);%正态函数
end
function z=Kernel_Thin_plate(R,s)
%R距离
z=R.^2.*log(R);%thin_plate
end
function z=Kernel_LinearEpsR(R,s)
%R距离
%s大概和采样点间距差不多就行，可以略大（更胖）
s=2*s;%这里要更大
z=s-R;%线性函数
z(z<0)=0;
end
function IsInShape=IsPointInShape3(A,points)
%判断点是否在某个三维凸多面体内
%A，凸多面体的顶点。points，N行3列。
%例子：A=[0,0,0;0,0,1;0,1,0;0,1,1;1,0,0;1,0,1;1,1,0;1,1,1];points=rand(1000,3)*3-1;
%IsInShape=IsPointInShape3(A,points)
NPoints=size(points,1);%计算有多少个点
IsInShape=false(NPoints,1);
NConvhull=size(A,1);%计算凸包上有多少个点
BD_A=[min(A,[],1);max(A,[],1)];
for kp=1:NPoints
P_k=points(kp,:);
if any(P_k<BD_A(1,:)) || any(P_k>BD_A(2,:)) %如果超过A的矩形边界，说明肯定不在A内
continue
end
NewA=[A;P_k];%把这个点加入新凸包计算
NewP=max(unique(convhull(NewA,'Simplify',false)));%查看新凸包这个点会不会涉及到新点
IsInShape(kp)=(NewP==NConvhull);
end
end
