【数据结构】 栈（Stack）的应用场景

news2024/9/24 23:27:59

文章目录

  • 🌏前言
  • 🍀改变元素的序列
    • 🚩场景一
      • 📌解析：
    • 🚩场景二
      • 📌解析：
  • 🎍将递归转化为循环
  • 🌳[括号匹配](https://leetcode.cn/problems/valid-parentheses/)
    • 🚩题目描述：
    • 🚩示例：
    • 🚩思路解析：
    • 🚩代码实现：
  • 🎄[逆波兰表达式求值](https://leetcode.cn/problems/evaluate-reverse-polish-notation/)
    • 🐱‍👤拓展逆波兰式
      • 🐱‍👓什么叫做逆波兰表达式
      • 🐱‍🐉逆波兰表达式算法步骤
    • 🚩题目描述
    • 🚩示例：
    • 🚩解法思路
  • 🌴[出栈入栈次序匹配](https://www.nowcoder.com/practice/d77d11405cc7470d82554cb392585106?tpId=13&&tqId=11174&rp=1&ru=/activity/oj&qru=/ta/coding-interviews/question-ranking)
    • 🚩题目描述：
    • 🚩示例
    • 🚩解法思路：
    • 🚩代码实现：
  • 🌲[最小栈](https://leetcode.cn/problems/min-stack/description/)
    • 🚩题目描述：
    • 🚩示例：
    • 🚩思路解析：
      • 📌将元素val推入堆栈
      • 📌删除堆栈顶部的元素
      • 📌获取堆栈顶部的元素
      • 📌获取堆栈中的最小元素
    • 🚩完整代码：
  • ⭕总结

🌏前言

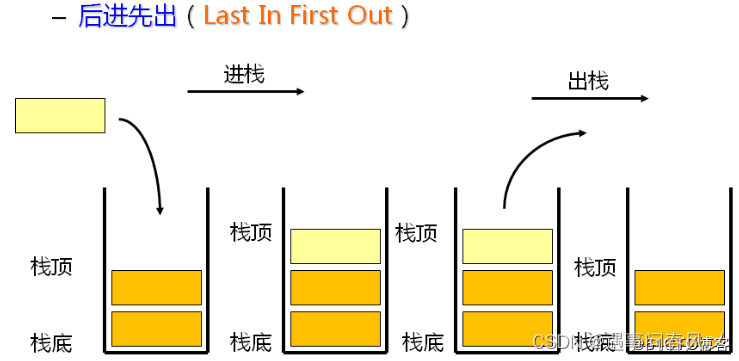
栈（Stack）又名堆栈，作为一个== 先进后出== 的数据结构。

它是一种运算受限的线性表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。
在这里插入图片描述

🍀改变元素的序列

🚩场景一

  1. 若进栈序列为 1,2,3,4 ，进栈过程中可以出栈，则下列不可能的一个出栈序列是（C）
    A: 1,4,3,2 B: 2,3,4,1 C: 3,1,4,2 D: 3,4,2,1

📌解析：

  • A选项进出入栈顺序：
  • push(1)->push(2)->push(3)->push(4)->pop(4)->pop(3)->pop(2);
  • B选型的出入栈顺序：
  • push(1)->push(2)->pop(2)->push(3)->pop(3)->push(4)->pop(4)->pop(1);
  • C选项出入栈顺序：
  • push(1)->push(2)->push(3)->pop(3)------->？pop(1)
  • 这时候我们的我们的栈内元素为：
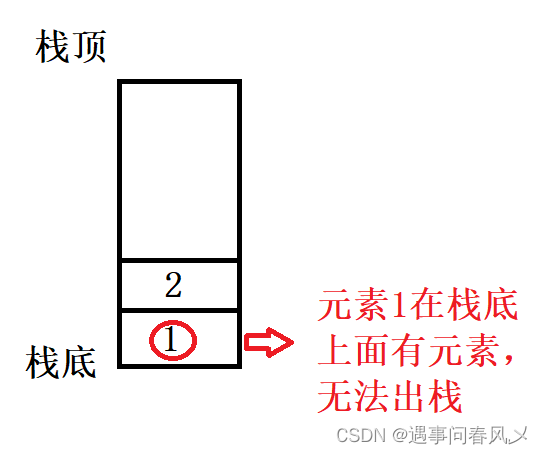
  • 在这里插入图片描述
  • 所以C选项错误
  • D选项出入栈顺序：
  • pusn(1)->push(2)->push(3)->pop(3)->push(4)->pop(4)->pop(2)->pop(1);

🚩场景二

  1. 一个栈的初始状态为空。现将元素1、2、3、4、5、A、B、C、D、E依次入栈，然后再依次出栈，则元素出栈的顺序是（ B ）。
    A: 12345ABCDE B: EDCBA54321
    C: ABCDE12345 D: 54321EDCBA

📌解析：

依次入栈后，栈内元素为：
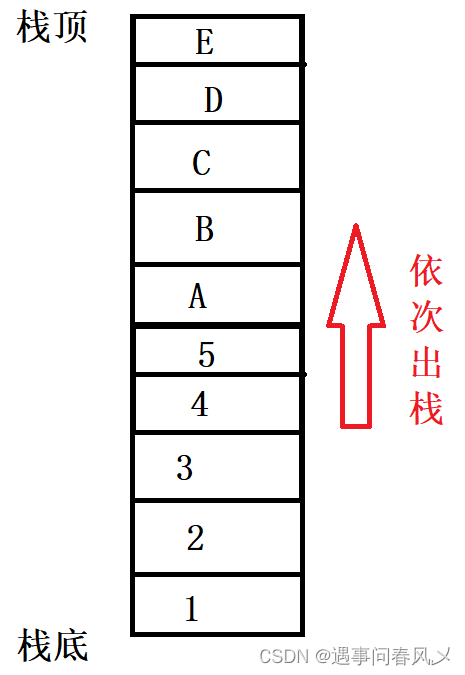
在这里插入图片描述
所以答案为B；

🎍将递归转化为循环

比如：逆序打印链表

在我们没有学习栈以前，我们可能会使用递归的方法进行打印，如下所示：

    // 递归方式
    void printList(Node head){
        if(null != head){
            printList1(head.next);
            System.out.print(head.val + " ");
        }
    }
    // 循环方式
    void printList1(Node head) {
        if (null == head) {
            return;
        }
    }

其实我们发现逆序打印链表的本质不就是：排在前面的后打印，排在后面的先打印

这不就是栈先进后出的思想吗

所以我们可以先让链表的每一个依次进栈，再出栈即可，实现如下：

        Stack<Node> s = new Stack<>();
// 将链表中的结点保存在栈中
        Node cur = head;
        while(null != cur){
            s.push(cur);
            cur = cur.next;
        }
        // 将栈中的元素出栈
        while(!s.empty()){
            System.out.print(s.pop().val + " ");
        }

🌳括号匹配

🚩题目描述：

给定一个只包括 ‘(’，‘)’，‘{’，‘}’，‘[’，‘]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。
  3. 每个右括号都有一个对应的相同类型的左括号。
class Solution {
    public boolean isValid(String s) {
        
    }
}

🚩示例：

在这里插入图片描述

🚩思路解析：

我们利用栈的方法进行解决：

  • 如果是左括号，就让他进栈
  • 如果是右括号，就让它与栈顶元素进行比较
  • 如果栈顶元素与该右括号构成一对，则让栈顶元素出栈
  • 若不是一对，则返回false；

特殊情况考虑：

  • 右括号进来时栈为空，此时直接返回false就好
  • 左括号太多，遍历完后，栈内还有元素，这时候需要进行为空的判断
  • 若为空，返回true；反之则为false；

🚩代码实现：

class Solution {
    public boolean isValid(String s) {
        Stack<Character> characterStack = new Stack<>();
        for(int i = 0;i < s.length(); i++) {
            char ch1 = s.charAt(i);
            if(ch1 == '('||ch1 == '{' || ch1 == '[') {
                characterStack.push(ch1);
            } else {
                if(characterStack.empty()) {
                    return false;
                }
                char ch2 = characterStack.peek();
                if(ch2 == '('&&ch1 == ')' ||ch2 == '{'&&ch1 == '}' ||ch2 == '['&&ch1 == ']') {
                    characterStack.pop();
                } else {
                    return false;
                }
            }
        }
       if(characterStack.empty()) {
            return true;
        }
        return false;
    }
}

🎄逆波兰表达式求值

🐱‍👤拓展逆波兰式

🐱‍👓什么叫做逆波兰表达式

逻辑提问式类似于算术表达式，对于检索而言，这种表达式并不是最优和最简洁的形式，需要进行必要的转换。

1929年波兰的逻辑学家卢卡西维兹(Jan Lucasiewicz)提出了将运算符放在运算项后面的逻辑表达式，又称“逆波兰表达式”。

采用这种表达式组织逻辑提问式非常方便检索运算，是日本的福岛先生最早将逆波兰表达式应用于情报检索的，故又称为“福岛方法”。 [2]

逆波兰表达式又叫做后缀表达式，是一种没有括号，并严格遵循“从左到右”运算的后缀式表达方法，如下表所示：
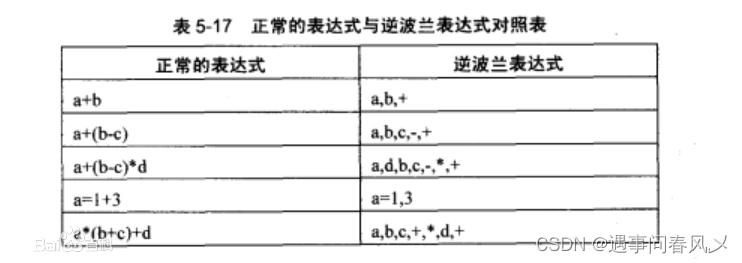
在这里插入图片描述

🐱‍🐉逆波兰表达式算法步骤

  1. 首先构造一个运算符栈，此运算符在栈内遵循越往栈顶优先级越高的原则。

  2. 读入一个用中缀表示的简单算术表达式，为方便起见，设该简单算术表达式的右端多加上了优先级最低的特殊符号“#”。

  3. 从左至右扫描该算术表达式，从第一个字符开始判断，如果该字符是数字，则分析到该数字串的结束并将该数字串直接输出。

  4. 如果不是数字，该字符则是运算符，此时需比较优先关系。具体做法是：将该字符与运算符栈顶的运算符的优先关系相比较。如果该字符优先关系高于此运算符栈顶的运算符，则将该运算符入栈。若不是的话，则将栈顶的运算符从栈中弹出，直到栈项运算符的优先级低于当前运算符，将该字符入栈。

  5. 重复步骤1～2，直至扫描完整个简单算术表达式，确定所有字符都得到正确处理，便可以将中缀式表示的简单算术表达式转化为逆波兰表示的简单算术表达式。

🚩题目描述

给你一个字符串数组 tokens ，表示一个根据 逆波兰表示法 表示的算术表达式。

请你计算该表达式。返回一个表示表达式值的整数。

🚨注意：

  • 有效的算符为 ‘+’、‘-’、‘*’ 和 ‘/’ 。
  • 每个操作数（运算对象）都可以是一个整数或者另一个表达式。
  • 两个整数之间的除法总是 向零截断 。
  • 表达式中不含除零运算。
  • 输入是一个根据逆波兰表示法表示的算术表达式。
  • 答案及所有中间计算结果可以用 32 位 整数表示。
class Solution {
    public int evalRPN(String[] tokens) {

    }
}

🚩示例：

在这里插入图片描述

🚩解法思路

如果当前字符为数字，则压栈，如果是运算符，则将栈顶两个元素弹出作相应运算，结果再入栈，最后当表达式扫描完后，栈里的就是结果。

🚨注意：先出来的数为左操作数，后出来的数为右操作数

代码实现如下：

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        for(String x : tokens){
            if(!isOperation(x)) {
                stack.push(Integer.parseInt(x));
            }else {
                int num2 = stack.pop();
                int num1 = stack.pop();
                switch (x) {
                    case "+":
                        stack.push(num1+num2);
                        break;
                    case "-":
                        stack.push(num1-num2);
                        break;
                    case "*":
                        stack.push(num1*num2);
                        break;
                    case "/":
                        stack.push(num1/num2);
                        break;
                }
            }
        }
        return stack.pop();
    }
    private boolean isOperation(String x) {
        if (x.equals("+") || x.equals("-") || x.equals("/") || x.equals("*")) {
            return true;
        }
        return false;
    }
    
}

🌴出栈入栈次序匹配

🚩题目描述：

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。

  1. 0<=pushV.length == popV.length <=1000
  2. -1000<=pushV[i]<=1000
  3. pushV 的所有数字均不相同

🚩示例

在这里插入图片描述

🚩解法思路：

我们就可以用一个栈来模拟。对于入栈序列，只要栈为空，序列肯定要依次入栈。那什么时候出来呢？自然是遇到一个元素等于当前的出栈序列的元素，那我们就放弃入栈，让它先出来。

具体做法：

  • 准备一个辅助栈，两个下标分别访问两个序列。
  • 辅助栈为空或者栈顶不等于出栈数组当前元素，就持续将入栈数组加入栈中。
  • 栈顶等于出栈数组当前元素就出栈。
  • 当入栈数组访问完，出栈数组无法依次弹出，就是不匹配的，否则两个序列都访问完就是匹配的。
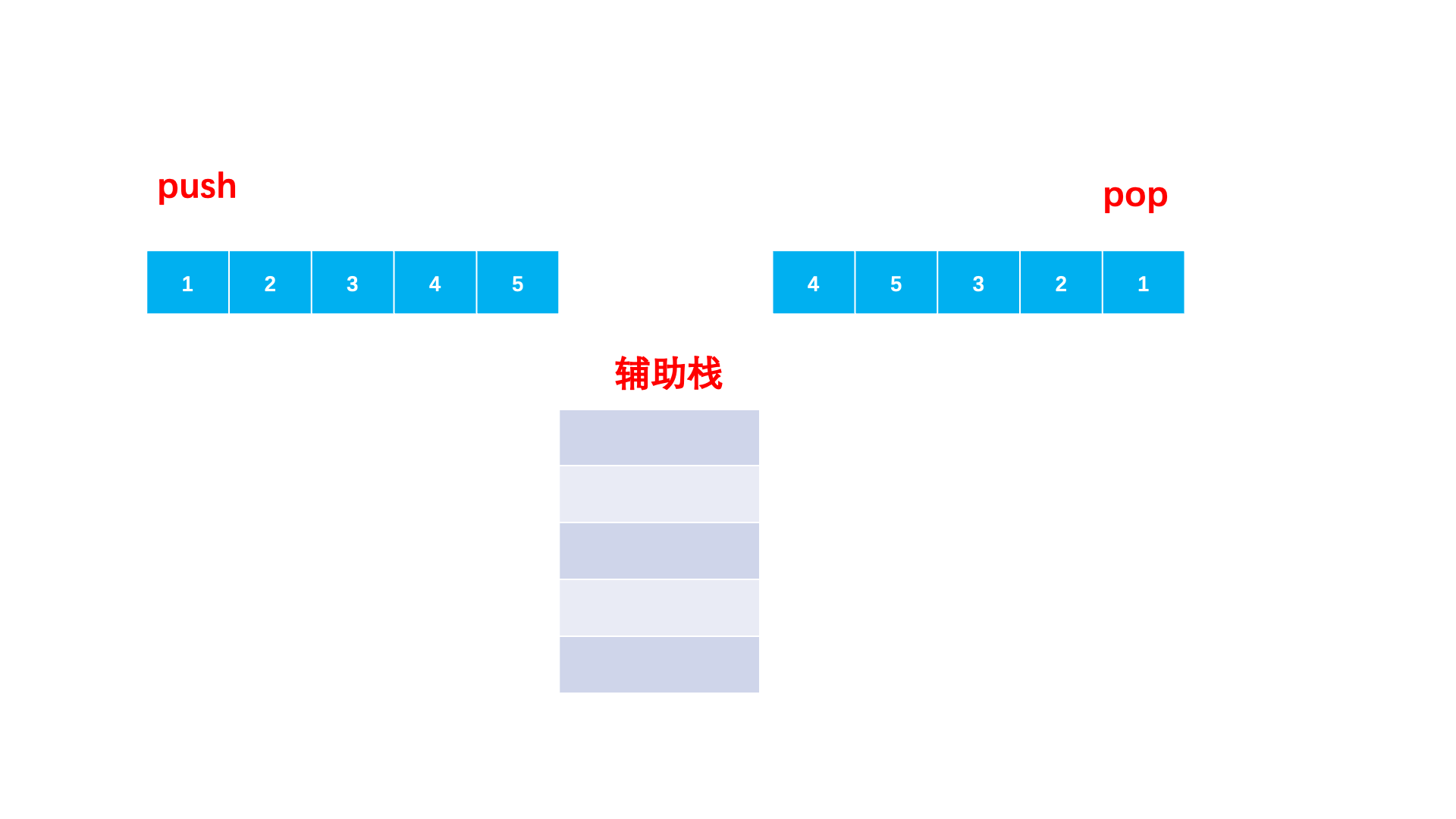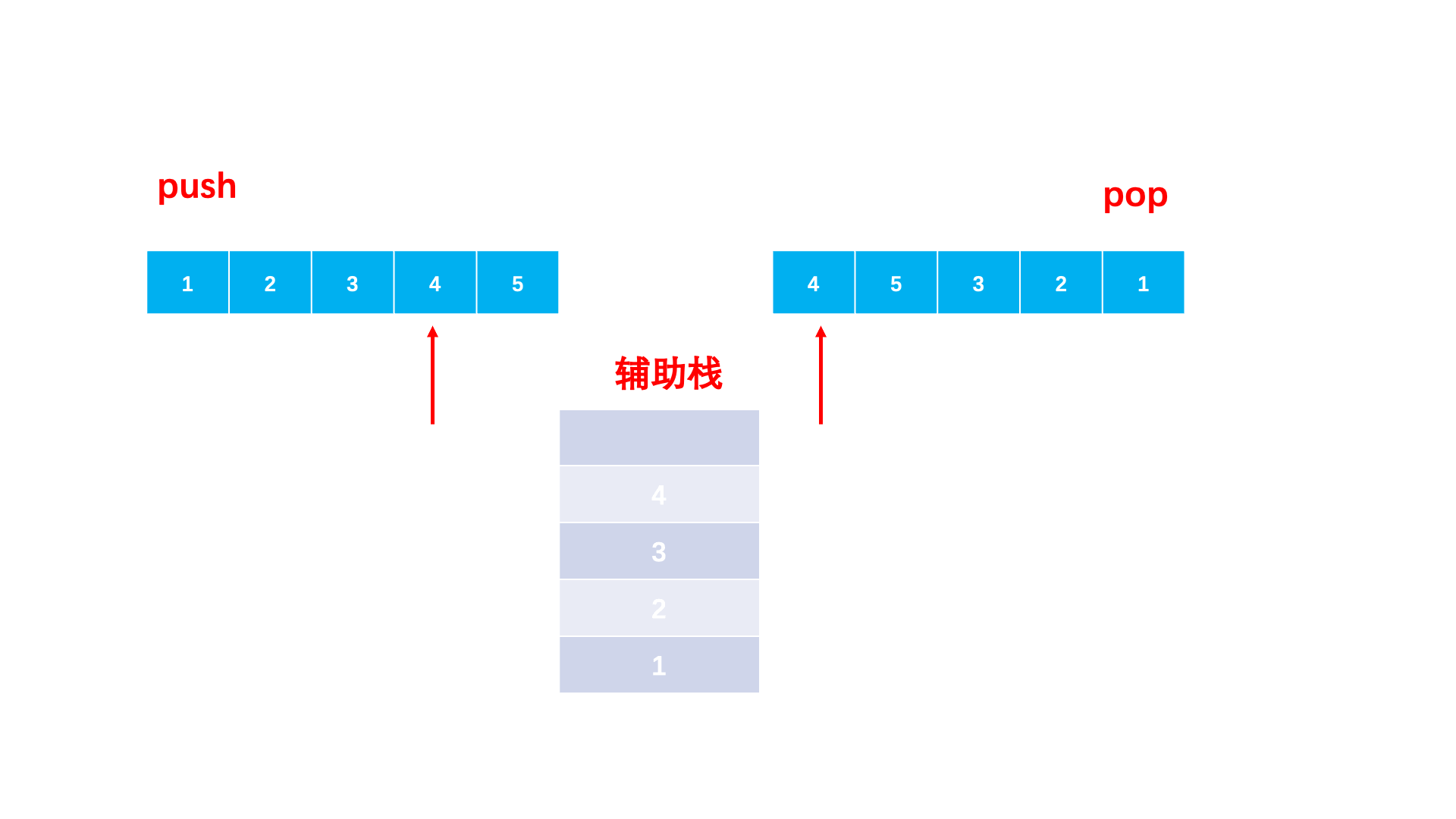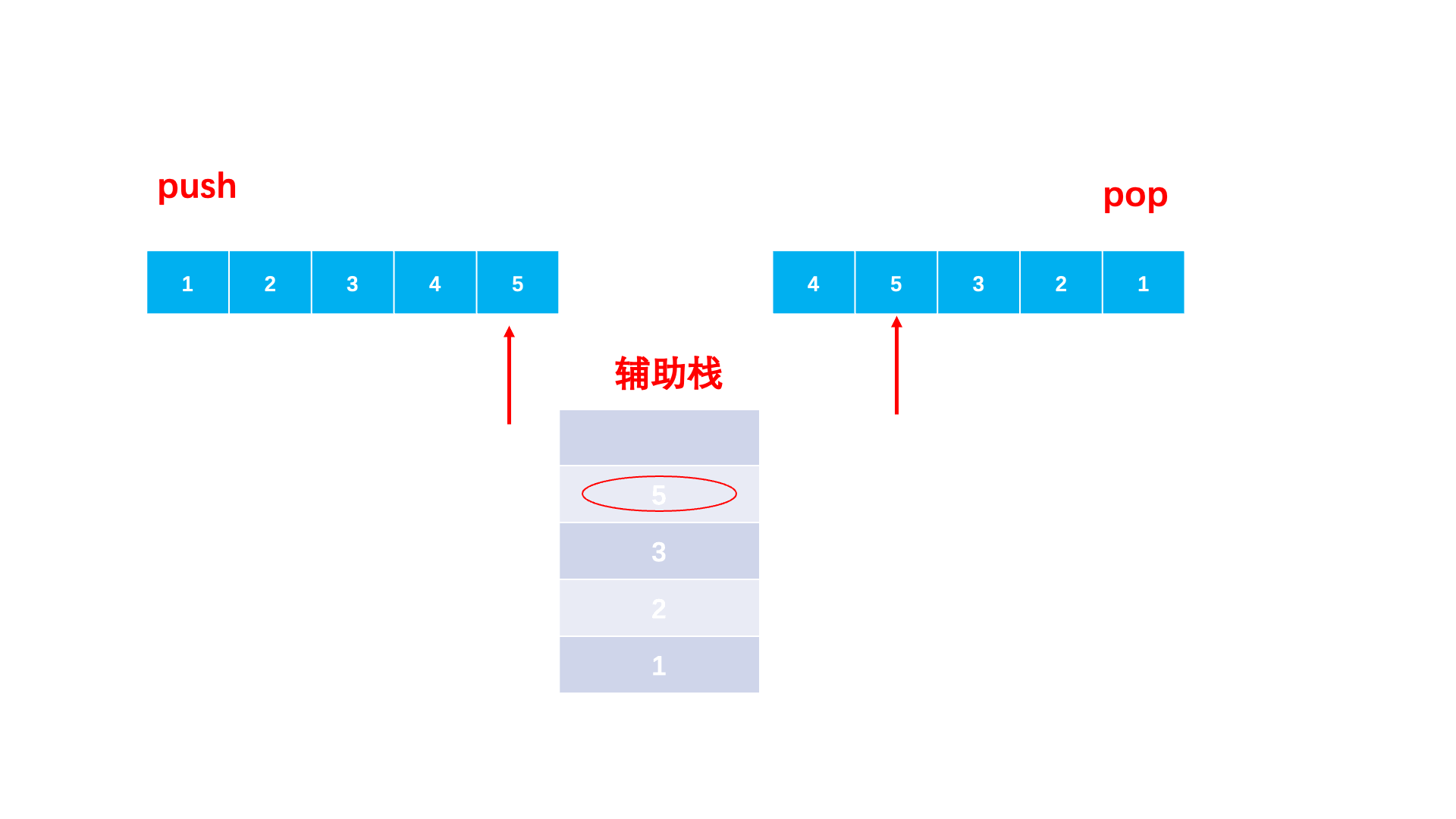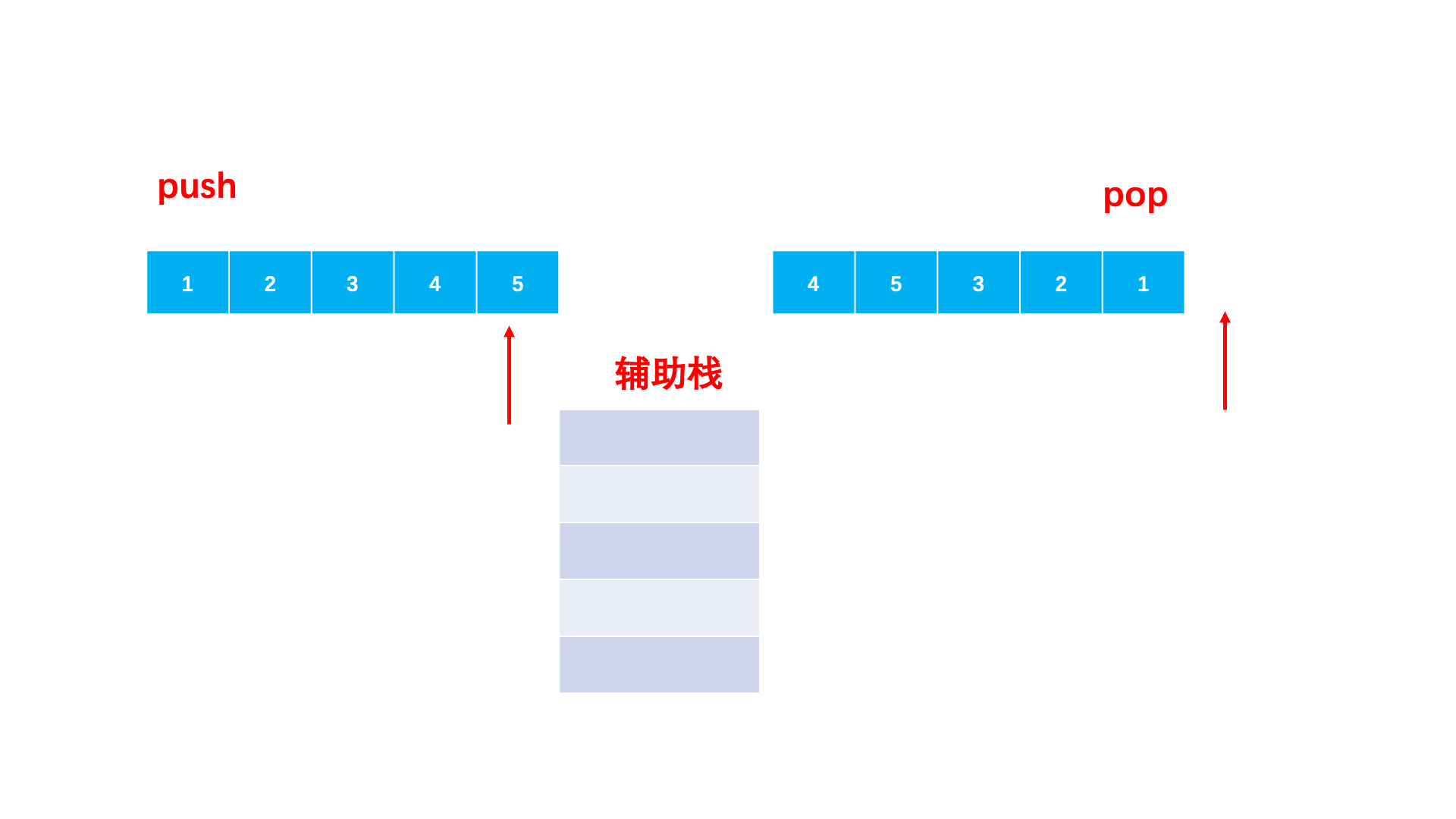
    在这里插入图片描述

🚩代码实现：

import java.util.Stack;
public class Solution {
    public boolean IsPopOrder(int [] pushA,int [] popA) {
        int n = pushA.length;
        //辅助栈
        Stack<Integer> s = new Stack<>();
        //遍历入栈的下标
        int j = 0;
        //遍历出栈的数组
        for(int i = 0; i < n; i++){
            //入栈：栈为空或者栈顶不等于出栈数组
            while(j < n && (s.isEmpty() || s.peek() != popA[i])){
                s.push(pushA[j]);
                j++;
            }
            //栈顶等于出栈数组
            if(s.peek() == popA[i])
                s.pop();
            //不匹配序列
            else
                return false;
        }
        return true;
    }
}

🌲最小栈

🚩题目描述：

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

  • MinStack() 初始化堆栈对象。
  • void push(int val) 将元素val推入堆栈。
  • void pop() 删除堆栈顶部的元素。
  • int top() 获取堆栈顶部的元素。
  • int getMin() 获取堆栈中的最小元素。
class MinStack {

    public MinStack() {

    }
    
    public void push(int val) {

    }
    
    public void pop() {

    }
    
    public int top() {

    }
    
    public int getMin() {

    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

🚩示例：

在这里插入图片描述

🚩思路解析：

我们创建两个栈

  • 一个用来存放我们的全部数据->stack
  • 一个用来存放最小栈->minStack
	private Stack<Integer> stack ;
    private Stack<Integer> minStack ;
    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }

📌将元素val推入堆栈

做法如下：

  • stack无差别推入
  • 对于minStack进行判断，若为空，直接压入
  • 若不为空，则需要与栈顶元素进行比较
  • 若小于等于，则压入

代码实现如下：

    public void push(int val) {
        stack.push(val);
        if(minStack.empty()) {
            minStack.push(val);
        }else {
            if(val <= minStack.peek()) {
                minStack.push(val);
            }
        }
    }

📌删除堆栈顶部的元素

做法如下：

  • 对stack进行判断判断，若不为空。怎进行删除
  • 同样我们的minStack也需要进行判断，判断条件为：若栈顶元素等于stack所删除元素
  • 则minStack栈顶元素也要删除，目的时维护最小栈

代码实现如下:

    public void pop() {
        if(!stack.empty()) {
            Integer val = stack.pop();
            //维护最小栈
            if (val.equals(minStack.peek())) {
                minStack.pop();
            }
        }
    }

📌获取堆栈顶部的元素

  • 做一个是否为空的判断

  • 若不为直接返回栈顶元素就好

  • 若为空返回-1

代码实现如下：

    // peek
    public int top() {
        if(!stack.empty()) {
            return stack.peek();
        }
        return -1;
    }

📌获取堆栈中的最小元素

直接返回minStack栈顶元素就好

    public int getMin() {
        return minStack.peek();
    }

🚩完整代码：

class MinStack {

    private Stack<Integer> stack ;
    private Stack<Integer> minStack ;
    public MinStack() {
        stack = new Stack<>();
        minStack = new Stack<>();
    }
    
    public void push(int val) {
        stack.push(val);
        if(minStack.empty()) {
            minStack.push(val);
        }else {
            if(val <= minStack.peek()) {
                minStack.push(val);
            }
        }
    }
    
    public void pop() {
        if(!stack.empty()) {
            Integer val = stack.pop();
            //维护最小栈
            if (val.equals(minStack.peek())) {
                minStack.pop();
            }
        }
    }
    // peek
    public int top() {
        if(!stack.empty()) {
            return stack.peek();
        }
        return -1;
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(val);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.getMin();
 */

⭕总结

关于《【数据结构】 栈（Stack）的应用场景》就讲解到这儿，感谢大家的支持，欢迎各位留言交流以及批评指正，如果文章对您有帮助或者觉得作者写的还不错可以点一下关注，点赞，收藏支持一下！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/930560.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

指针-C语言（初阶）

指针-C语言（初阶）

目录 一、什么是指针 二、指针和指针类型 2.1 指针-整数 2.2 指针的解引用 三、野指针 3.1 野指针形成原因 3.2 如何规避野指针 四、指针运算 4.1 指针-整数 4.2 指针-指针 4.3 指针的关系运算 五、指针和数组 六、二级指针 七、指针数组 一、什么是指针 指针是内存中一个…
阅读更多...
k-近邻算法概述,k-means与k-NN的区别对比

k-近邻算法概述,k-means与k-NN的区别对比

目录 k-近邻算法概述 k-近邻算法细节 k值的选取 分类器的决策 k-means与k-NN的区别对比 k-近邻算法概述 k近邻&#xff08;k-nearest neighbor, k-NN&#xff09;算法由 Cover 和 Hart 于1968年提出&#xff0c;是一种简单的分类方法。通俗来说&#xff0c;就是给定一个…
阅读更多...
Linux操作系统--网络配置(2)

Linux操作系统--网络配置(2)

在上一次课程中，我们对Linux课程中的网络有了一个了解，下面我们来看看如何配置网络IP。 1.配置网络IP地址 在Linux操作系统中，比如搭建集群，这一个时候如果使用DHCP实现动态IP的分配，那么如果需要访问管理其中一个节点操作时候，就需要通过其IP访问。这一个时候还得去查看…
阅读更多...
十五、systemctl命令如何使用？

十五、systemctl命令如何使用？

在Linux系统中&#xff0c;一些内置服务可以通过systemctl控制&#xff0c;部分第三方软件也可以通过systemctl控制。 1、基础语法 start&#xff1a;开启服务&#xff1b; stop&#xff1a;关闭服务&#xff1b; status&#xff1a;查看服务当前状态&#xff1b; enable&a…
阅读更多...
【推荐】Spring与Mybatis集成整合

【推荐】Spring与Mybatis集成整合

目录 1.概述 2.集成 2.1代码演示&#xff1a; 3.整合 3.1概述 3.2 进行整合分页 接着上两篇&#xff0c;我已经写了Mybatis动态之灵活使用&#xff0c;mybatis的分页和特殊字符的使用方式接下来把它们集成起来&#xff0c;是如何的呢&#x1f447;&#x1f447;&#x1…
阅读更多...
Stm32的时钟系统以及使用SysTick滴答定时器实现延时

Stm32的时钟系统以及使用SysTick滴答定时器实现延时

前言 STM32的时钟系统由多个时钟源和时钟树组成时钟源包括主时钟源&#xff08;HSE&#xff09;、内部高速时钟源&#xff08;HSI&#xff09;、内部低速时钟源&#xff08;LSI&#xff09;和外部低速时钟源&#xff08;LSE&#xff09;。时钟树由多个时钟分频器和时钟门控器组…
阅读更多...
五、多表查询-2.概述分类

五、多表查询-2.概述分类

一、多表查询概述 二、演示 1、准备数据 &#xff08;1&#xff09;创建emp1表并注入数据&#xff0c;添加外键&#xff1a; 2、多表查询 一共 102条数据&#xff1a;17个员工&#xff0c;6个部门&#xff0c;176102 3、消除笛卡尔积 一共16条记录&#xff1a; 为啥17个员工&…
阅读更多...
Aos插件实现滚动动画效果

Aos插件实现滚动动画效果

aos文档 aos使用感受跟wow相似&#xff0c;但比wow多了浏览器回滚&#xff0c;动画效果会再次展现 安装 npm install aos使用 main.js全局导入css import aos/dist/aos.cssvue文件 <template><div class"box"><div class"code" v-for&q…
阅读更多...
Java接收json参数

Java接收json参数

JSON 并不是唯一能够实现在互联网中传输数据的方式&#xff0c;除此之外还有一种 XML 格式。JSON 和 XML 能够执行许多相同的任务&#xff0c;那么我们为什么要使用 JSON&#xff0c;而不是 XML 呢&#xff1f; 之所以使用 JSON&#xff0c;最主要的原因是 JavaScript。众所周知…
阅读更多...
搭建 Qt6 开发环境

搭建 Qt6 开发环境

作者&#xff1a; 一去、二三里 个人微信号&#xff1a; iwaleon 微信公众号&#xff1a; 高效程序员 Qt 是一个跨平台的 C 应用程序开发框架&#xff0c;它提供了丰富的组件库和工具&#xff0c;使得开发人员可以在各种平台上轻松地开发 GUI 应用程序。 由于我们的教程 《细说…
阅读更多...
嵌入式设备应用开发（发现需求和提升价值）

嵌入式设备应用开发（发现需求和提升价值）

【 声明：版权所有，欢迎转载，请勿用于商业用途。 联系信箱：feixiaoxing @163.com】 很多做技术的同学，都会陷入到技术的窠臼之中。对于如何做具体的产品、实现具体的技术，他们可能很感兴趣。但是做出来的东西做什么用，或者说是有没有竞争力，事实上他们不是很关心…
阅读更多...
二叉搜索树-----红黑树

二叉搜索树-----红黑树

✅<1>主页&#xff1a;我的代码爱吃辣&#x1f4c3;<2>知识讲解&#xff1a;数据结构——红黑树☂️<3>开发环境&#xff1a;Visual Studio 2022&#x1f4ac;<4>前言&#xff1a;红黑树也是一颗二叉搜索树&#xff0c;其作为map&#xff0c;set的底层…
阅读更多...
AttributeError: module ‘torchvision.io.image‘ has no attribute ‘ImageReadMode‘

AttributeError: module ‘torchvision.io.image‘ has no attribute ‘ImageReadMode‘

我的torch和torchvision版本 import torch torch.__version__‘1.7.1cu110’ import torchvision torchvision.__version__‘0.8.2cu110’ 原代码 mode torchvision.io.image.ImageReadMode.RGB labels.append(torchvision.io.read_image(os.path.join(voc_dir, Segmentat…
阅读更多...
文生图模型之Stable Diffusion

文生图模型之Stable Diffusion

原始文章地址 autoencoder CLIP text encoder tokenizer最大长度为77&#xff08;CLIP训练时所采用的设置&#xff09;&#xff0c;当输入text的tokens数量超过77后&#xff0c;将进行截断&#xff0c;如果不足则进行paddings&#xff0c;这样将保证无论输入任何长度的文本&…
阅读更多...
Vue2向Vue3过度核心技术综合案例

Vue2向Vue3过度核心技术综合案例

目录 1 面经基础版-案例效果分析1.面经效果演示2.功能分析3.实现思路分析&#xff1a;配置路由功能实现 2 面经基础版-一级路由配置3 面经基础版-二级路由配置1.使用场景2.语法3.代码实现 4 面经基础版-二级导航高亮1.实现思路2.代码实现 5 面经基础版-首页请求渲染1.步骤分析2…
阅读更多...
新开通的抖店体验分太低，达人不愿意合作怎么办？解决办法如下

新开通的抖店体验分太低，达人不愿意合作怎么办？解决办法如下

我是王路飞。 找达人带货的玩法是最适合新手抖店商家的&#xff0c;同时也是最适合长线去玩的方法。 但是新手前期找达人的时候&#xff0c;会有一个难点&#xff0c;就是自己的抖店因为是新开通的&#xff0c;所以要么没体验分&#xff0c;要么就是体验分太低了&#xff0c;…
阅读更多...
崔东树：汽车行业正在迎来令人兴奋的时代，智能座舱推动私车普及

崔东树：汽车行业正在迎来令人兴奋的时代，智能座舱推动私车普及

随着新能源汽车和智能座舱的不断发展&#xff0c;汽车行业正经历着一场革命性的变革。当前&#xff0c;不仅汽车电动化的进程在加速推进&#xff0c;智能座舱的升级与完善也成为了行业的热点话题。崔东树指出&#xff0c;随着汽车电动化和智能化的发展&#xff0c;智能座舱的快…
阅读更多...
学习高等数学需要的初等数学知识

学习高等数学需要的初等数学知识

文章目录 名词解释常用希腊字符读音幂、根式和对数常用的三角函数值三角函数变换一元二次方程求解充分条件和必要条件切线方程、斜率和法线隐函数极坐标排列组合 名词解释 教材中存在着许多熟悉且陌生的词汇&#xff0c;作者在此进行了整理&#xff1a; 概念&#xff1a;概念…
阅读更多...
开始MySQL之路—— DDL语法、DML语法、DQL语法基本操作详解

开始MySQL之路—— DDL语法、DML语法、DQL语法基本操作详解

DDL语法 DDL&#xff08;Data Definition Language&#xff09; 数据定义语言&#xff0c;该语言部分包括以下内容。 对数据库的常用操作 对表结构的常用操作 修改表结构 对数据库的常用操作 1: 查看当前所有的数据库 show databases; 2&#xff1a;创建数据库 create dat…
阅读更多...
Linux下的Shell基础——流程控制（三）

Linux下的Shell基础——流程控制（三）

前言&#xff1a; 每门编程都有它独特的语法&#xff0c;比如C语言&#xff0c;Java等编程语言&#xff0c;有相同的地方也有自己独特的地方&#xff0c;但都离不开变量、运算符&#xff0c;条件判断、循环和函数这几个地方的学习&#xff0c;下面就让我们学习一下shell编程里…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023