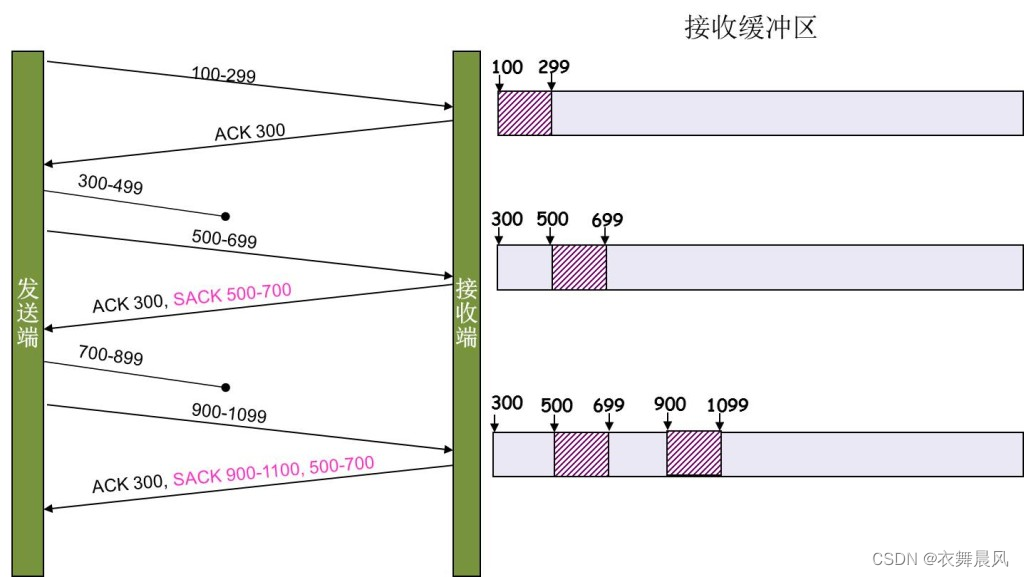
文章目录
- 名词解释
- 常用希腊字符读音
- 幂、根式和对数
- 常用的三角函数值
- 三角函数变换
- 一元二次方程求解
- 充分条件和必要条件
- 切线方程、斜率和法线
- 隐函数
- 极坐标
- 排列组合
名词解释
教材中存在着许多熟悉且陌生的词汇,作者在此进行了整理:
- 概念:概念是人类在认识过程中,从感性认识上升到理性认识,把所感知的事物的共同本质特点抽象出来,加以概括,是自我认知意识的一种表达,形成概念式思维惯性。
- 定义:定义是对一种事物的本质特征或一个概念的内涵和外延的确切而简要的说明;或是透过列出一个事件或者一个物件的基本属性来描述或规范一个词或一个概念的意义。
- 公理:公理是不能也不需要被证明,被大家公认的直接可以使用的道理。
- 定理:定理是可以被证明而且已经通过其他公理和定理证明出来的道理。
- 性质:事物本身所具有的、区别于其他事物的特征。
常用希腊字符读音
- α \alpha α:/ælfə/
- β \beta β:/betə/
- Γ \Gamma Γ、 γ \gamma γ:/gama/
- Δ \Delta Δ、 δ \delta δ:/deltə/
- ε \varepsilon ε:/epsilon/
- υ \upsilon υ:/apsilon/
- θ \theta θ:/θitə/
- π \pi π:/paɪ/
- η \eta η:/ita/
- Λ \Lambda Λ、 λ \lambda λ:/læmdə/
- μ \mu μ:/mju/
- ξ \xi ξ:/ksi/
- Σ \Sigma Σ、 σ \sigma σ:/sigmə/
- τ \tau τ:/taʊ/
- Φ \varPhi Φ、 φ \varphi φ:/faɪ/
- ψ \psi ψ:/psi/
- Ω \Omega Ω、 ω \omega ω:/omiga/
- ρ \rho ρ:/ru:/
幂、根式和对数
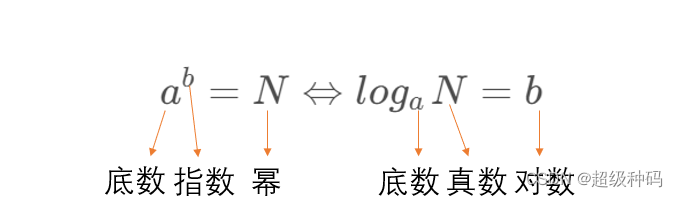
- 幂运算:
a m a n = a m + n a m ÷ a n = a m − n ( a m ) n = a m n ( a b ) m = a m b m ( a b ) m = a m b m a m + n = a m a n a − m = 1 a m ( m ∈ N + , a ≠ 0 ) a 1 m = a m ( 当 m 为偶数时 a ≥ 0 ; m 为奇数时 a ∈ R ) a^ma^n=a^{m+n}\\ a^m\div a^n=a^{m-n}\\ (a^m)^n=a^{mn}\\ (ab)^m=a^mb^m\\ (\frac{a}{b})^m=\frac{a^m}{b^m}\\ a^{m+n}=a^ma^n\\ a^{-m}=\frac{1}{a^m}(m\in N^+,a\ne0)\\ a^{\frac{1}{m}}=\sqrt[m]{a}(当m为偶数时a\ge 0;m为奇数时a\in R) aman=am+nam÷an=am−n(am)n=amn(ab)m=ambm(ba)m=bmamam+n=amana−m=am1(m∈N+,a=0)am1=ma(当m为偶数时a≥0;m为奇数时a∈R) - 根式运算:
a 2 = a a 2 = ∣ a ∣ a b = a b a b = a b \sqrt{a}^2=a\\ \sqrt{a^2}=|a|\\ \sqrt{ab}=\sqrt{a}\sqrt{b}\\ \sqrt{\frac{a}{b}}=\frac{\sqrt a}{\sqrt b} a2=aa2=∣a∣ab=abba=ba - 对数运算:
a l o g a N = N l o g a M N = l o g a M + l o g a N l o g a N n = n l o g a N l o g a m N = 1 m l o g a N l o g a N = l o g c N l o g c a alog_aN=N\\ log_aMN=log_aM+log_aN\\ log_aN^n=nlog_aN\\ log_{a^m}N=\frac{1}{m}log_aN\\ log_aN=\frac{log_cN}{log_ca} alogaN=NlogaMN=logaM+logaNlogaNn=nlogaNlogamN=m1logaNlogaN=logcalogcN
常用的三角函数值
| 函数/角度 | 0 | 30 | 45 | 60 | 90 |
|---|---|---|---|---|---|
| sin | 0 | 1 2 \frac{1}{2} 21 | 2 2 \frac{\sqrt2}{2} 22 | 3 2 \frac{\sqrt3}{2} 23 | 1 |
| cos | 1 | 3 2 \frac{\sqrt3}{2} 23 | 2 2 \frac{\sqrt2}{2} 22 | 1 2 \frac{1}{2} 21 | 0 |
| tan | 0 | 3 3 \frac{\sqrt3}{3} 33 | 1 | 3 \sqrt3 3 | - |
三角函数变换
- 三角函数关系式:
t a n a c o t a = 1 s i n a c s c a = 1 c o s a s e c a = 1 t a n a = s i n a c o s a c o t a = c o s a s i n a s i n a + c o s a = 1 1 + t a n 2 a = s e c 2 a 1 + c o t 2 a = c s c 2 a tanacota=1\\ sinacsca=1\\ cosaseca=1\\ tana=\frac{sina}{cosa}\\ cota=\frac{cosa}{sina}\\ sin^a+cos^a=1\\ 1+tan^2a=sec^2a\\ 1+cot^2a=csc^2a tanacota=1sinacsca=1cosaseca=1tana=cosasinacota=sinacosasina+cosa=11+tan2a=sec2a1+cot2a=csc2a - 诱导公式:
| 角\函数 | s i n sin sin | c o s cos cos | t a n tan tan | c o t cot cot |
|---|---|---|---|---|
| − a -a −a | − s i n a -sina −sina | c o s a cosa cosa | − t a n a -tana −tana | − c o t a -cota −cota |
| π 2 − a \frac{\pi}{2}-a 2π−a | c o s a cosa cosa | s i n a sina sina | c o t a cota cota | t a n a tana tana |
| π 2 + a \frac{\pi}{2}+a 2π+a | c o s a cosa cosa | − s i n a -sina −sina | − c o t a -cota −cota | − t a n a -tana −tana |
| π − a \pi-a π−a | s i n a sina sina | − c o s a -cosa −cosa | − t a n a -tana −tana | − c o t a -cota −cota |
| π + a \pi+a π+a | − s i n a -sina −sina | − c o s a -cosa −cosa | t a n a tana tana | c o t a cota cota |
| 3 π 4 − a \frac{3\pi}{4}-a 43π−a | − c o s a -cosa −cosa | − s i n a -sina −sina | c o t a cota cota | t a n a tana tana |
| 3 π 4 + a \frac{3\pi}{4}+a 43π+a | − c o s a -cosa −cosa | s i n a sina sina | − c o t a -cota −cota | − t a n a -tana −tana |
| π − a \pi-a π−a | − s i n a -sina −sina | c o s a cosa cosa | − t a n a -tana −tana | − c o t a -cota −cota |
| π + a \pi+a π+a | s i n a sina sina | c o s a cosa cosa | t a n a tana tana | c o t a cota cota |
-
和差角公式:
s i n ( a ± b ) = s i n a c o s b ± c o s a s i n b c o s ( a + b ) = c o s a c o s b ∓ s i n a s i n b t a n ( a ± b ) = t a n a ± t a n b 1 ∓ t a n a t a n b c o t ( a ± b ) = c o t a c o t b ∓ 1 c o t b ± c o t a sin(a\pm b)=sinacosb\pm cosasinb\\ cos(a+b)=cosacosb\mp sinasinb\\ tan(a\pm b)=\frac{tana\pm tanb}{1\mp tanatanb}\\ cot(a\pm b)=\frac{cotacotb\mp 1}{cotb\pm cota} sin(a±b)=sinacosb±cosasinbcos(a+b)=cosacosb∓sinasinbtan(a±b)=1∓tanatanbtana±tanbcot(a±b)=cotb±cotacotacotb∓1 -
和差化积公式:
s i n a + s i n b = 2 s i n a + b 2 c o s a − b 2 s i n a − s i n b = 2 c o s a + b 2 s i n a − b 2 c o s a + c o s b = 2 c o s a + b 2 c o s a − b 2 c o s a − c o s b = − 2 s i n a + b 2 s i n a − b 2 sina+sinb=2sin\frac{a+b}{2}cos\frac{a-b}{2}\\ sina-sinb=2cos\frac{a+b}{2}sin\frac{a-b}{2}\\ cosa+cosb=2cos\frac{a+b}{2}cos\frac{a-b}{2}\\ cosa-cosb=-2sin\frac{a+b}{2}sin\frac{a-b}{2} sina+sinb=2sin2a+bcos2a−bsina−sinb=2cos2a+bsin2a−bcosa+cosb=2cos2a+bcos2a−bcosa−cosb=−2sin2a+bsin2a−b -
积化和差公式:
s i n a s i n b = − 1 2 [ c o s ( a + b ) − c o s ( a − b ) ] c o s a c o s b = 1 2 [ c o s ( a + b ) + c o s ( a − b ) ] s i n a c o s b = 1 2 [ s i n ( a + b ) + s i n ( a − b ) ] c o s a s i n b = 1 2 [ s i n ( a + b ) − s i n ( a − b ) ] sinasinb=-\frac{1}{2}[cos(a+b)-cos(a-b)]\\cosacosb=\frac{1}{2}[cos(a+b)+cos(a-b)]\\sinacosb=\frac{1}{2}[sin(a+b)+sin(a-b)]\\cosasinb=\frac{1}{2}[sin(a+b)-sin(a-b)] sinasinb=−21[cos(a+b)−cos(a−b)]cosacosb=21[cos(a+b)+cos(a−b)]sinacosb=21[sin(a+b)+sin(a−b)]cosasinb=21[sin(a+b)−sin(a−b)] -
倍角公式:
s i n 2 a = 2 s i n a c o s a s i n 3 a = 3 s i n a − 4 s i n 3 a c o s 2 a = 2 c o s 2 a − 1 = 1 − 2 s i n 2 a = c o s 2 a − s i n 2 a c o s 3 a = 4 c o s 3 a − 3 c o s a c o t 2 a = c o t 2 a − 1 2 c o t a t a n 2 a = 2 t a n a 1 − t a n 2 a sin2a=2sinacosa\\ sin3a=3sina-4sin^3a\\ cos2a=2cos^2a-1=1-2sin^2a=cos^2a-sin^2a\\ cos3a=4cos^3a-3cosa\\ cot2a=\frac{cot^2a-1}{2cota}\\ tan2a=\frac{2tana}{1-tan^2a} sin2a=2sinacosasin3a=3sina−4sin3acos2a=2cos2a−1=1−2sin2a=cos2a−sin2acos3a=4cos3a−3cosacot2a=2cotacot2a−1tan2a=1−tan2a2tana -
半角公式:
s i n a 2 = ± 1 − c o s a 2 c o s a 2 = ± 1 + c o s a 2 t a n a 2 = ± 1 − c o s a 1 + c o s a = 1 − c o s a s i n a = s i n a 1 + c o s a c o t a 2 = ± 1 + c o s a 1 − c o s a = 1 + c o s a s i n a = s i n a 1 − c o s a sin\frac{a}{2}=\pm\sqrt{\frac{1-cosa}{2}}\\ cos\frac{a}{2}=\pm\sqrt{\frac{1+cosa}{2}}\\ tan\frac{a}{2}=\pm\sqrt{\frac{1-cosa}{1+cosa}}=\frac{1-cosa}{sina}=\frac{sina}{1+cosa}\\ cot\frac{a}{2}=\pm\sqrt{\frac{1+cosa}{1-cosa}}=\frac{1+cosa}{sina}=\frac{sina}{1-cosa} sin2a=±21−cosacos2a=±21+cosatan2a=±1+cosa1−cosa=sina1−cosa=1+cosasinacot2a=±1−cosa1+cosa=sina1+cosa=1−cosasina -
万能公式:
s i n a = 2 t a n a 2 1 + t a n 2 a 2 c o s a = 1 − t a n 2 a 2 1 + t a n 2 a 2 t a n a = 2 t a n a 2 1 − t a n 2 a 2 sina=\frac{2tan\frac{a}{2}}{1+tan^2\frac{a}{2}}\\ cosa=\frac{1-tan^2\frac{a}{2}}{1+tan^2\frac{a}{2}}\\ tana=\frac{2tan\frac{a}{2}}{1-tan^2\frac{a}{2}} sina=1+tan22a2tan2acosa=1+tan22a1−tan22atana=1−tan22a2tan2a -
其它公式:
a s i n a + b c o s a = a 2 + b 2 s i n ( a + c ) , 其中 t a n c = b a a s i n a − b c o s a = a 2 + b 2 c o s ( a − c ) , 其中 t a n c = a b 1 + s i n a = ( s i n a 2 + c o s a 2 ) 2 1 − s i n a = ( s i n a 2 − c o s a 2 ) 2 asina+bcosa=\sqrt{a^2+b^2}sin(a+c),其中tanc=\frac{b}{a}\\ asina-bcosa=\sqrt{a^2+b^2}cos(a-c),其中tanc=\frac{a}{b}\\ 1+sina=(sin\frac{a}{2}+cos\frac{a}{2})^2\\ 1-sina=(sin\frac{a}{2}-cos\frac{a}{2})^2 asina+bcosa=a2+b2sin(a+c),其中tanc=abasina−bcosa=a2+b2cos(a−c),其中tanc=ba1+sina=(sin2a+cos2a)21−sina=(sin2a−cos2a)2
一元二次方程求解

充分条件和必要条件
- 充分条件:由前一个条件推出后一个条件。
- 必要条件:由后一个条件推出前一个条件。
- 充要条件:前一个条件能推出后一个条件,后一个条件也能推出前一个条件。
切线方程、斜率和法线
- 切线指的是一条刚好触碰到曲线上某一点的直线。更准确地说,当切线经过曲线上的某点(即切点)时,切线的方向与曲线上该点的方向是相同的。
- 斜率:表示直线关于坐标轴倾斜程度的量。通常用直线与横坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。
- k = t a n θ k=tan\theta k=tanθ
- k = y 1 − y 2 x 1 − x 2 k=\frac{y_1-y_2}{x_1-x_2} k=x1−x2y1−y2
- 法线:法线就是垂直于切线的线。
- 函数在某一点的切线斜率乘法线斜率等于负一。
- 已知直线方程求斜率: a x + b y + c = 0 ⇒ k = − a b ax+by+c=0\Rightarrow k=-\frac{a}{b} ax+by+c=0⇒k=−ba
- 已知斜率和一点求直线: y − y 0 = k ( x − x 0 ) y-y_0=k(x-x_0) y−y0=k(x−x0)
隐函数
如果方程 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0能确定 y y y是 x x x的函数,那么称这种方式表示的函数是隐函数。而函数就是指:在某一变化过程中,两个变量 x 、 y x、y x、y,对于某一范围内的 x x x的每一个值, y y y都有确定的值和它对应, y y y就是 x x x的函数。这种关系一般用 y = f ( x ) y=f(x) y=f(x)即显函数来表示。 F ( x , y ) = 0 F(x,y)=0 F(x,y)=0即隐函数是相对于显函数来说的。
极坐标
- 极坐标:极坐标是指在平面内取一个定点 O O O,叫极点,引一条射线 O x Ox Ox,叫做极轴,再选定一个长度单位和角度的正方向(通常取逆时针方向)。对于平面内任何一点 M M M,用 ρ ρ ρ表示线段 O M OM OM的长度, θ θ θ表示从 O x Ox Ox到 O M OM OM的角度, ρ ρ ρ叫做点 M M M的极径, θ θ θ叫做点 M M M的极角,有序数对 ( ρ , θ ) (ρ,θ) (ρ,θ)就叫点 M M M的极坐标,这样建立的坐标系叫做极坐标系。
- 参数方程:一般地,在平面直角坐标系中,如果曲线上任意一点的坐标 x 、 y x、y x、y都是某个变数 t t t的函数,并且对于 t t t的每一个允许的取值,由方程组确定的点 ( x , y ) (x, y) (x,y)都在这条曲线上,那么这个方程就叫做曲线的参数方程,联系变数 x 、 y x、y x、y的变数 t t t叫做参变数,简称参数。相对而言,直接给出点坐标间关系的方程即称为普通方程。
- 极坐标和直角坐标的相互转换:
- x = ρ c o s θ x=\rho cos\theta x=ρcosθ
- y = ρ s i n θ y=\rho sin\theta y=ρsinθ
- t a n θ = y x tan\theta=\frac{y}{x} tanθ=xy
排列组合
分类计数原理(加法原理):完成一件事,有 n n n类办法,在第一类办法中有 m 1 m_1 m1种不同的方法,在第二类办法中有 m 2 m_2 m2种不同的方法, … \dots …,在第 n n n类办法中有 m n m_n mn种不同的方法,那么完成这件事共有 N = m 1 + m 2 + … … + m n N=m_1+m_2+……+m_n N=m1+m2+……+mn种不同的方法。
分步计数原理(乘法原理):完成一件事,需要分成 n n n个步骤,做第 1 1 1步有 m 1 m_1 m1种不同的方法,做第 2 2 2步有 m 2 m_2 m2种不同的方法, … \dots …,做第 n n n步有 m n m_n mn种不同的方法,那么完成这件事共有 N = m 1 × m 2 × … … × m n N=m_1×m_2×……×m_n N=m1×m2×……×mn种不同的方法。
排列:定义:从 n n n个不同元素中取出 m ( m ≤ n ) m(m≤n) m(m≤n)个按照一定顺序排成一列,叫做从 n n n个不同元素中取出 m m m个元素的一个排列。
排列数:从 n n n个不同元素中取出 m ( m ≤ n ) m(m≤n) m(m≤n)个的所有排列的个数,叫做从 n n n个不同元素中取出 m m m个元素的排列数,记作 A n m A_n^m Anm
公式:
- A n m = n ! ( n − m ) ! A_n^m=\frac{n!}{(n-m)!} Anm=(n−m)!n!
- A n n = n ! A_n^n=n! Ann=n!
- $ A_n^0=1$
- 0 ! = 1 0!=1 0!=1
组合:
定义:一般地,从 n n n个不同元素中取出 m ( m ≤ n ) m(m≤n) m(m≤n)个元素合成一组,叫做从 n n n个不同元素中取出 m m m个元素的一个组合。
组合数:从 n n n个不同元素中取出 m ( m ≤ n ) m(m≤n) m(m≤n)个元素的所有不同组合的个数,叫做从 n n n个不同元素中取出 m m m个元素的组合数,记作 C n m C_n^m Cnm
公式:
- C n m = n ! m ! ( n − m ) ! C_n^m=\frac{n!}{m!(n-m)!} Cnm=m!(n−m)!n!
- C n m = c n n − m C_n^m=c_n^{n-m} Cnm=cnn−m
- C n + 1 m = C n m + C n m − 1 C_{n+1}^m=C_n^m+C_n^{m-1} Cn+1m=Cnm+Cnm−1
- C n 0 = 1 C_n^0=1 Cn0=1