二分查找
1、基础版
public static int binarySearch(int[] a, int target) {
int i = 0, j = a.length - 1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) { // 在左边
j = m - 1;
} else if (a[m] < target) { // 在右边
i = m + 1;
} else {
return m;
}
}
return -1;
}
i 是插入点
2、左闭右开区间
核心:j索引位置的元素,一定不是要查找的元素
public static int binarySearch(int[] a, int target) {
int i = 0, j = a.length;
while (i < j) {
int m = (i + j) >>> 1;
if (target < a[m]) { // 在左边
j = m;
} else if (a[m] < target) { // 在右边
i = m + 1;
} else {
return m;
}
}
return -1;
}
3、平衡版
问题:当查找的元素在数组最左边或者最右边时,就会导致不平衡
public static int binarySearchBalance(int[] a, int target) {
int i = 0, j = a.length;
while (1 < j - i) { //j-i是指还未被比较的元素个数,只有一个时,直接跳出循环
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m;
} else {
i = m;
}
}
return (a[i] == target) ? i : -1;
}
优点:循环内比较次数少了
缺点:必须等退出循环了才能得到结果
注意:i不能等于m+1,因为else的情况包括target==a[m],如果i=m+1,那就略过了这个正确的查询结果
4、二分查找 Java 版
private static int binarySearch0(long[] a, int fromIndex, int toIndex,
long key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
long midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
- 例如
[
1
,
3
,
5
,
6
]
[1,3,5,6]
[1,3,5,6] 要插入
2
2
2 ,那么就是找到一个位置,这个位置左侧元素都比它小
- 等循环结束,若没找到,low 左侧元素肯定都比 target 小,因此 low 即插入点
- 插入点取负是为了与找到情况区分
- -1 是为了把索引 0 位置的插入点与找到的情况进行区分
5、最左/最右
-
对于数组 [ 1 , 2 , 3 , 4 , 4 , 5 , 6 , 7 ] [1, 2, 3, 4, 4, 5, 6, 7] [1,2,3,4,4,5,6,7],查找元素4,结果是索引3
-
对于数组 [ 1 , 2 , 4 , 4 , 4 , 5 , 6 , 7 ] [1, 2, 4, 4, 4, 5, 6, 7] [1,2,4,4,4,5,6,7],查找元素4,结果也是索引3,并不是最左侧的元素
如果希望返回的是要查找的元素中最左侧元素
public static int binarySearchLeftmost1(int[] a, int target) {
int i = 0, j = a.length - 1;
int candidate = -1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m - 1;
} else if (a[m] < target) {
i = m + 1;
} else {
candidate = m; // 记录候选位置
j = m - 1; // 继续向左
}
}
return candidate;
}
如果希望返回的是要查找的元素中最右侧元素
public static int binarySearchRightmost1(int[] a, int target) {
int i = 0, j = a.length - 1;
int candidate = -1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m - 1;
} else if (a[m] < target) {
i = m + 1;
} else {
candidate = m; // 记录候选位置
i = m + 1; // 继续向右
}
}
return candidate;
}
6、最左/最右升级版
对于 Leftmost 与 Rightmost,可以返回一个比 -1 更有用的值
Leftmost 改为
public static int binarySearchLeftmost(int[] a, int target) {
int i = 0, j = a.length - 1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target <= a[m]) {
j = m - 1;
} else {
i = m + 1;
}
}
return i;
}
- leftmost 返回值的另一层含义: < t a r g e t \lt target <target 的元素个数
- 小于等于中间值,都要向左找
Rightmost 改为
public static int binarySearchRightmost(int[] a, int target) {
int i = 0, j = a.length - 1;
while (i <= j) {
int m = (i + j) >>> 1;
if (target < a[m]) {
j = m - 1;
} else {
i = m + 1;
}
}
return i - 1;
}
- 大于等于中间值,都要向右找
7、范围查询
- 查询 x < 4 x \lt 4 x<4, 0.. l e f t m o s t ( 4 ) − 1 0 .. leftmost(4) - 1 0..leftmost(4)−1
- 查询 x ≤ 4 x \leq 4 x≤4, 0.. r i g h t m o s t ( 4 ) 0 .. rightmost(4) 0..rightmost(4)
- 查询 4 < x 4 \lt x 4<x,$rightmost(4) + 1 … \infty $
- 查询 4 ≤ x 4 \leq x 4≤x, l e f t m o s t ( 4 ) . . ∞ leftmost(4) .. \infty leftmost(4)..∞
- 查询 4 ≤ x ≤ 7 4 \leq x \leq 7 4≤x≤7, l e f t m o s t ( 4 ) . . r i g h t m o s t ( 7 ) leftmost(4) .. rightmost(7) leftmost(4)..rightmost(7)
- 查询 4 < x < 7 4 \lt x \lt 7 4<x<7, r i g h t m o s t ( 4 ) + 1.. l e f t m o s t ( 7 ) − 1 rightmost(4)+1 .. leftmost(7)-1 rightmost(4)+1..leftmost(7)−1
8、求排名
l e f t m o s t ( t a r g e t ) + 1 leftmost(target) + 1 leftmost(target)+1
- t a r g e t target target 可以不存在,如: l e f t m o s t ( 5 ) + 1 = 6 leftmost(5)+1 = 6 leftmost(5)+1=6
- t a r g e t target target 也可以存在,如: l e f t m o s t ( 4 ) + 1 = 3 leftmost(4)+1 = 3 leftmost(4)+1=3
9、求前任
l e f t m o s t ( t a r g e t ) − 1 leftmost(target) - 1 leftmost(target)−1
- l e f t m o s t ( 3 ) − 1 = 1 leftmost(3) - 1 = 1 leftmost(3)−1=1,前任 a 1 = 2 a_1 = 2 a1=2
- l e f t m o s t ( 4 ) − 1 = 1 leftmost(4) - 1 = 1 leftmost(4)−1=1,前任 a 1 = 2 a_1 = 2 a1=2
10、求后任
r i g h t m o s t ( t a r g e t ) + 1 rightmost(target)+1 rightmost(target)+1
- r i g h t m o s t ( 5 ) + 1 = 5 rightmost(5) + 1 = 5 rightmost(5)+1=5,后任 a 5 = 7 a_5 = 7 a5=7
- r i g h t m o s t ( 4 ) + 1 = 5 rightmost(4) + 1 = 5 rightmost(4)+1=5,后任 a 5 = 7 a_5 = 7 a5=7
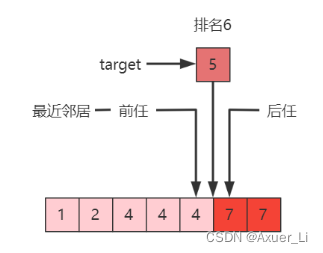
11、求最近邻居
- 前任和后任距离更近者
12、二分查找性能(复杂度)
下面分析二分查找算法的性能
时间复杂度
- 最坏情况: O ( log n ) O(\log n) O(logn)
- 最好情况:如果待查找元素恰好在数组中央,只需要循环一次 O ( 1 ) O(1) O(1)
空间复杂度
- 需要常数个指针 i , j , m i,j,m i,j,m,因此额外占用的空间是 O ( 1 ) O(1) O(1)