简介

🥥二分查找，又叫折半查找，通过找到数据二段性每次都能将原来的数据筛选掉一半，通过这个算法我们能够将一个一个查找的 O(n) 的时间复杂度优化到 O(logn) ，极大地提升了查找的效率。但使用二分进行查找必须要有一个前提，那就是查找的区间必须是有序的。如数组并非有序，则找不到该数组的的二段性。下面一起看看二分的基本步骤吧。

基本步骤

找一个区间 [L , R]，使答案一定在该区间中。
找一个判断条件，使得该判断条件具有二段性，并且答案一定是该二段性的分界点。
分析中点 mid 在该判断条件下是否成立，如果成立，考虑答案在哪个区间，如果不成立，答案在哪个区间。
如果更新方式为 R = mid, 则不做处理，若更新方式是L = mid，在计算 mid 时需要 +1。

第一种二分

🥥假设当前我们有一个 1~9 的有序数组，现在我们要查找数组中的7。由此我们可以通过数字的大小将其分为小于 7 和 大于等于 7 的两个部分。

🥥若算出来 mid 在左区间，由于其左边的值都是小于 7 的所以不需要保留，便可以将迭代区间缩短至 [mid+1,R] 。

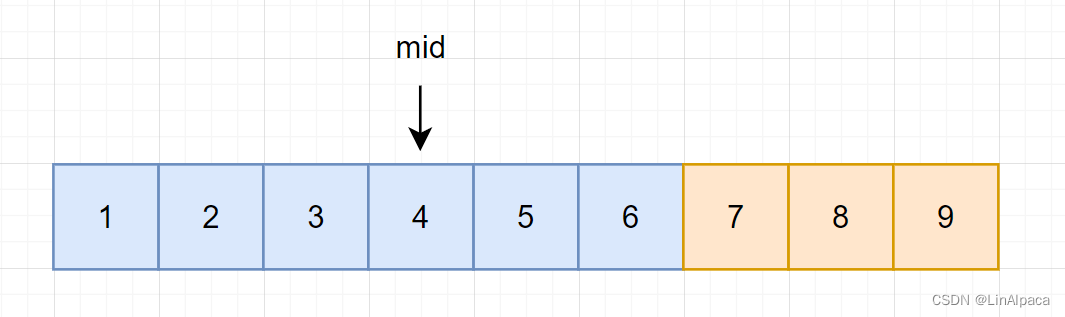
🥥而如果 mid 在右区间，这个区间的范围是大于等于 7 的，当前的值是有可能等于 7 的。

🥥所以需要将当前 mid 位保留，所以递增区间便保留至[L , mid]。

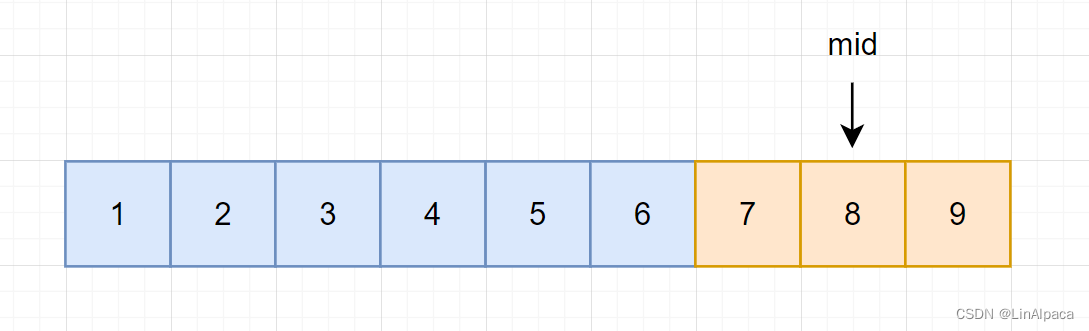
🥥并且根据上面的基本步骤的最后一步，因为更新方式为 R = mid , 则计算mid的时候不做处理。因此 mid = (L+R) / 2 。

int main()
{
	int arr[] = { 1,2,3,4,5,6,7,8,9 };
	int l = 0, r = 8,num = 7;
	while (l < r)
	{
		int mid = (l + r) / 2;  //迭代mid
		if (arr[mid] >= num)    //mid在右区间
		{
			r = mid;
		}
		else                    //mid在左区间
		{
			l = mid + 1;
		}
	}
	printf("%d\n", r);          //最后l和r一定相等
	return 0;
}

第二种二分

🥥与上面那种不一样，这次我们将原数组分作小于等于7，以及大于7的两部分。

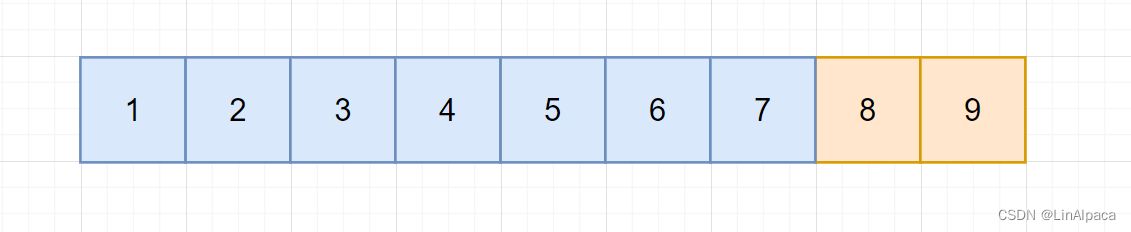
🥥且这次若 mid 在左区间，由于该区间都是小于等于目标值的，因此该部分的数据需要保留，由此迭代区间至 [mid, R] 。

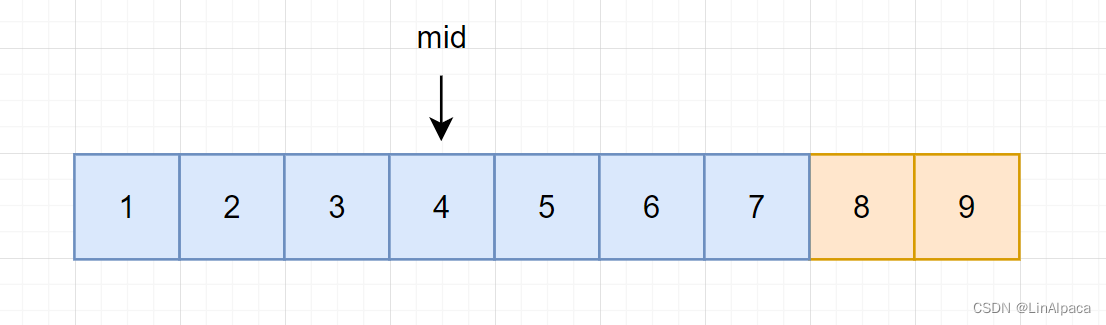
🥥而当 mid 在右区间时，由于右区间并没有我们所需要的值，所以可以不用保留，所以迭代区间至 [L,mid-1] 。

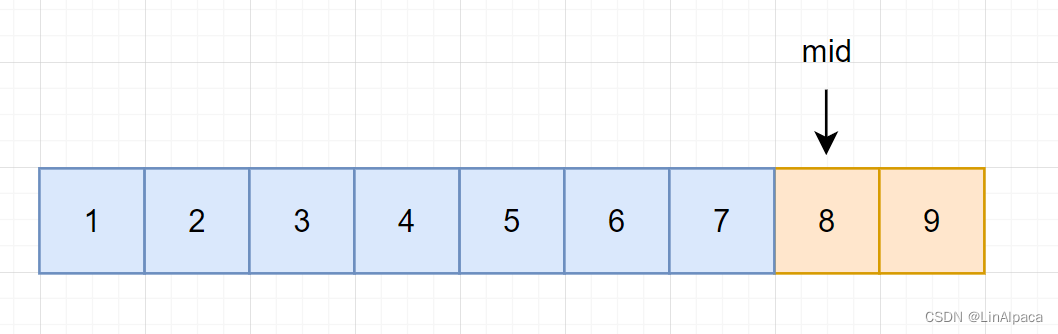
🥥而现在，由于我们使用 L = mid 进行区间的更新，因此在计算 mid 的时候还需要加上1。

int main()
{
	int arr[] = { 1,2,3,4,5,6,7,8,9 };
	int l = 0, r = 8,num = 7;
	while (l < r)
	{
		int mid = (l + r + 1) / 2;   //计算mid时要+1
		if (arr[mid] <= num)         //mid在左区间
		{
			l = mid;                 //区间缩至[mid,r]
		}
		else                         //mid在右区间
		{
			r = mid - 1;             //区间缩至[l,mid-1]
		} 
	}
	printf("%d\n", r);               //最后l一定等于r
	return 0;
}

🥥根据不同的二分法，二分查找有这两种不同的写法，因此在编写程序前，要先思考当前写法该如何迭代。mid 在左区间时是怎样一种情况，在右区间又是什么情况。考虑好迭代关系，最后再处理 mid 的计算就相当简单，且不容易出错了。

例题

搜索插入位置

传送门：搜索插入位置

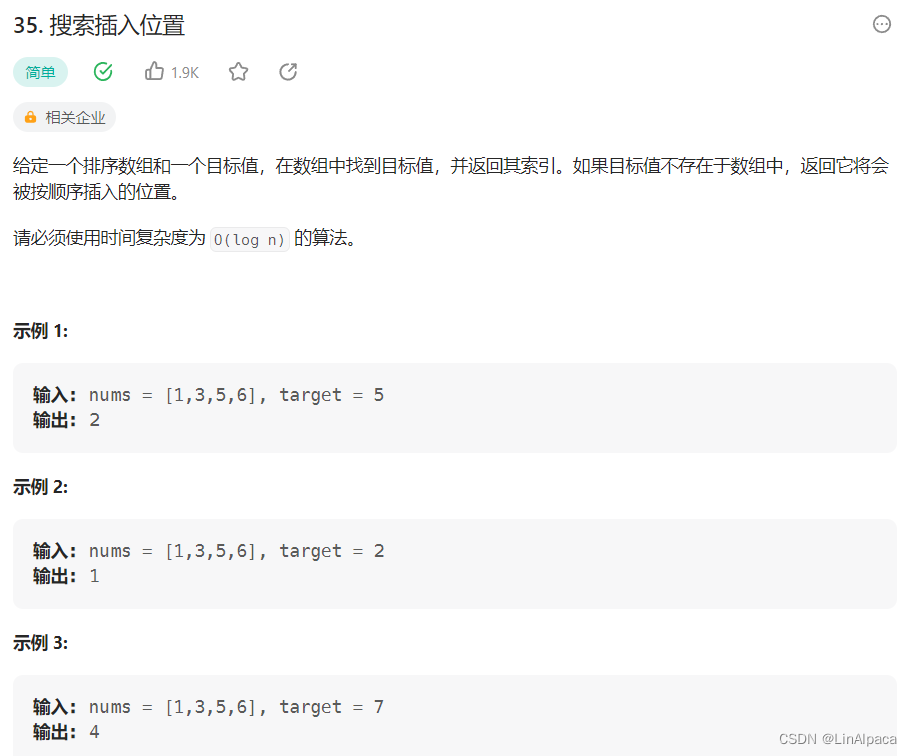
🥥这题难度相对简单，要我们在数组中找目标值，若找不到则返回目标值若插入到这个数组时的所在的下标。

🥥用我们上面的思路进行分析，我们不妨将数组分作小于目标值的以及大于等于目标值的两个区间。同时我们还要注意到目标值可能不存在或大于数组中的所有值，因此初始范围应当多扩展一位。由此便可得到代码。

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int l = 0,r = nums.size();
        while(l<r)
        {
            int mid = (l+r)/2;
            if (nums[mid] >= target)
		    {
			    r = mid;
		    }
		    else
		    {
			    l = mid + 1;
		    }
        }
        return r;
    }
};

数的范围

🥥传送门：AcWing 789. 数的范围

🥥通过读题我们可以知道，在这个数组之中有若干个重复的数，我们要根据题目找到一个数的区间，若无这个数则输出 -1 。但我们知道二分查找最后只能找一个数，那我们不妨这样想，因为这是个有序的数组，因此只要找到首尾两个端点就能够找到这个区间。

🥥而首尾两个点就能够用二分查找找到。分别是将数组由小于目标值和大于等于目标值、小于等于目标值和大于目标值两种分法进行划分，即进行两次二分查找，而这两次二分查找的两个分界点恰好就是一个区间的两个端点。

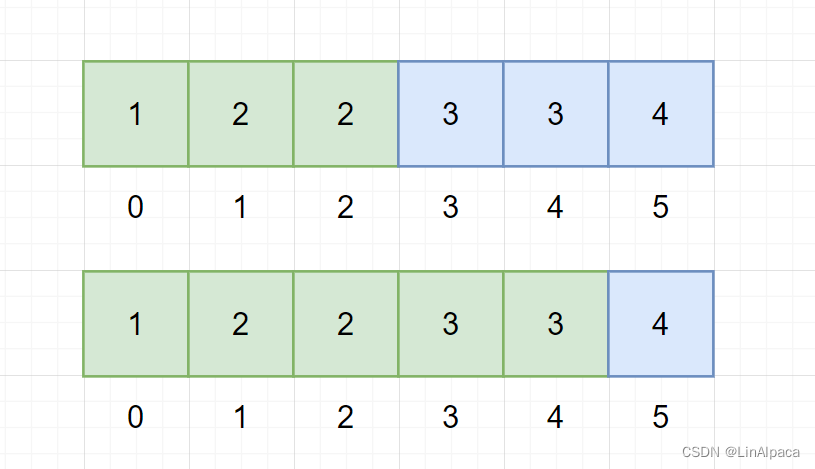
🥥即经过两次二分，分别查找左边界及右边界（若只有一个数则左右边界相等），查找一个边界后我们还可以进行一次特判，若当前端点并非我们要求的目标值，则说明这个数组之中并没有我们想要的值，因此便可以直接输出 -1 ，否则就再继续查找另一端点。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>

const int N = 100000;
int n, m;
int arr[N];

int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &arr[i]);
	}
	for (int i = 0; i < m; i++)  //  m组数据
	{
		int num;
		scanf("%d", &num);
		//求左端点
		int left = 0, right = n - 1;
		while (left < right)
		{
			int mid = (left + right) / 2;
			if (arr[mid] >= num)
			{
				right = mid;
			}
			else
			{
				left = mid + 1;
			}
		}
		if (arr[left] == num)
		{
			printf("%d ", left);
			//找右端点
			right = n - 1;
			while (left < right)
			{
				int mid = (left + right + 1) / 2;
				if (arr[mid] <= num)
				{
					left = mid;
				}
				else
				{
					right = mid - 1;
				}
			}
			printf("%d\n", left);
		}
		else
		{
			printf("-1 -1\n");
		}
	}
	return 0;
}