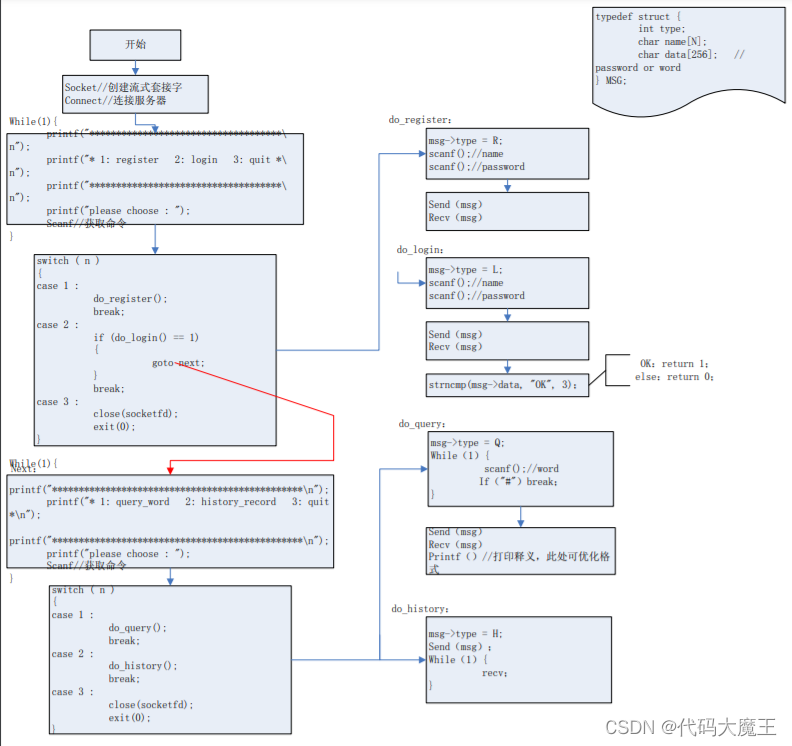
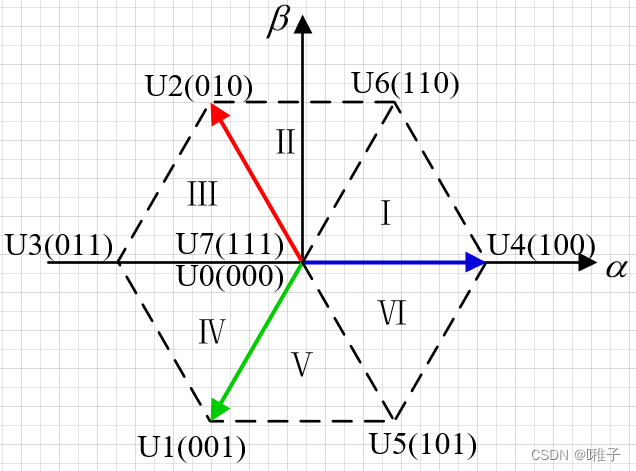
IMU根据其属性,可以知道其主要测量是线加速度和角加速度:
(1)
(2)
其中和
分别是线加速度偏差和角加速度偏差,可以利用随机游走模型建模,
,
,且符合高斯分布
;
和
是噪声,一般认为符合高斯分布
;
表示全球坐标下的重力加速度;
表示旋转变量,将
变换到t时刻坐标系下。我们可以得到从k到k+1时刻IMU的位置、速度和旋转为:
(3)
(4)
(5)
(6)
其中分别为第k时刻和第k+1时刻body在世界坐标系下的位置,速度和旋转;
代表t时刻body在
坐标系下的旋转四元数。
由于IMU状态量发生变化,就需要重新计算积分,且积分计算量大,所以提出了预积分,缓解计算量问题。参考系由世界坐标系转到坐标系,即(3)、(4)、(5)左乘
如下:
其中预计分为: