你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

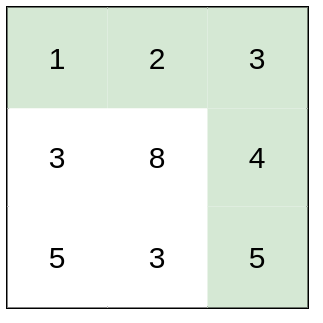
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

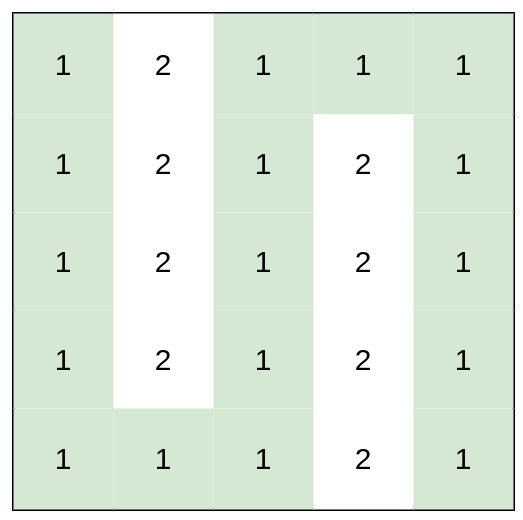
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

• rows == heights.length
• columns == heights[i].length
• 1 <= rows, columns <= 100
• 1 <= heights[i][j] <= 106

 

int minimumEffortPath(vector<vector<int>>& heights)
{
    int r = heights.size();
    int c = heights[0].size();
    vector<int> x{ -1,1,0,0 };
    vector<int> y{ 0,0,-1,1 };

    //最小值先出队
    auto tupleCmp = [](const auto& e1, const auto& e2) {
        return get<2>(e1) > get<2>(e2); 
    };
    priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, decltype(tupleCmp)> que(tupleCmp);
    que.emplace(0, 0, 0);

    vector<vector<bool>>visited(r+1, vector<bool>(c + 1, false));
    vector<int>ret(r *c+1, INT32_MAX);
    ret[0] = 0;
    while (!que.empty())
    {
        auto item = que.top();

        std::cout << get<2>(item) << std::endl;
        
        if (get<0>(item) == r - 1 && get<1>(item) == c - 1)
        {
            break;
        }
        que.pop();
        int row = get<0>(item);
        int col = get<1>(item);    
        if (visited[row][col] == true)
        {
            continue;
        }
        visited[row][col] = true;

        for (int i = 0; i < 4; i++)
        {
            if (row + x[i] < 0 || col + y[i] < 0 || row + x[i] >= heights.size()
                || col + y[i] >= heights[0].size())
            {
                continue;
            }
            
            int tmp = std::max(get<2>(item), abs(heights[row + x[i]][col + y[i]] - heights[row][col]));//保存之前最大值，get<2>(item)
            if (tmp < ret[(row + x[i])*c + col + y[i]])
            {
                ret[(row + x[i])*c + col + y[i]] = tmp;    
                que.emplace(row + x[i], col + y[i], tmp);
            }    
        }
    
    }
    return ret[r*c-1];

}