概念和性质:
强连通:在有向图G中,如果两个点u和v是互相可达的,即从u出发可以到达v,从v出发也可以到达u,则成u和v是强连通的。
强连通分量:如果一个有向图G不是强连通图,那么可以把它分成躲个子图,其中每个子图的内部是强连通的,而且这些子图已经扩展到最大,不能与子图外的任一点强连通,成这样的一个“极大连通”子图是G的一个强连通分量(SCC)。
强连通分量的一些性质:
(1)一个点必须有出度和入度,才会与其他点强连通。
(2)把一个SCC从图中挖掉,不影响其他点的强连通性。
求强连通分量的方法:
Kosaraju算法:
算法原理及步骤:
(1)将有向图G的所有边反向,建立返图rG,反图rG不会改变原图G的强连通性(也就不会改变SCC的数量)。
(2)对原图G做一次DFS,确定各点的先后顺序(可以用vector数组来记录顺序)。
(3)确定了顺序之后,在反图上做DFS,按顺序从优先级最高的点开始,到最低的点。
为什么要在反图上做DFS?这样做可以求得被隔离的岛。我们以下图为例,图a为原图G,图b为反图rG,我们将每个SCC都打上阴影,将其想象成一个个岛屿(也可以理解为一个个缩点),那么我们可以发现{a,b,e}这个SCC与其他SCC之间只有出边没有入边,所以这个SCC在第二次DFS中是要首先被遍历的,
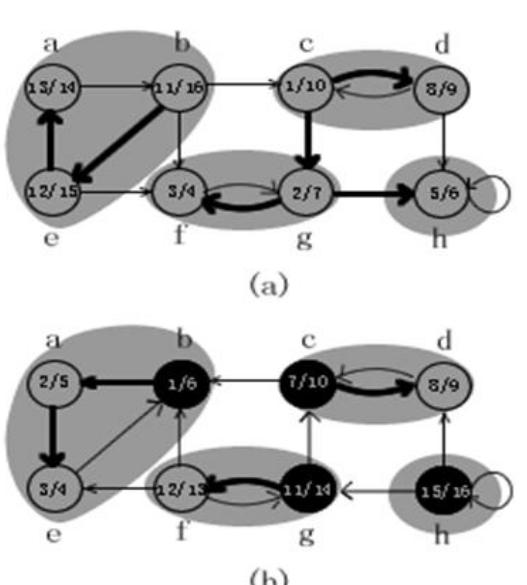
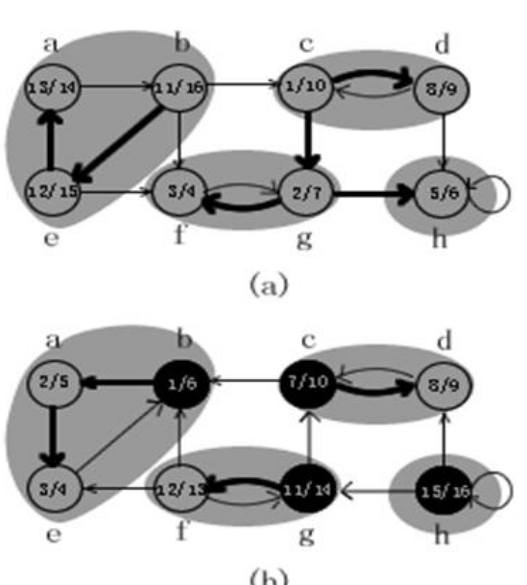
那么我们在反图上遍历它的好处就是,可以发现在反图中,{a,b,e}这个SCC变成了只有入边没有出边,所以我们的遍历一定只会被限制在当前的SCC中,确定了第一个SCC。当我们遍历完这个SCC,我们将其删除(在代码中可以体现为将其标记为已经遍历),然后继续从剩下的优先级最高的点开始搜索,这一次从c开始搜索,因为反边,这次搜索也被限制在{c,d}内,确定了第二个SCC,删除这个SCC,然后按照这个步骤确定剩下的SCC。
参考代码:
题目来自hdu 1269,标准的模板题,判断整个图是否强连通,求出SCC数量是否为1即可。
在进行第一次dfs确定先后顺序时,我们有在递归进入时和递归返回时标记两种方法。分别给出代码:
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e4 + 10;
const int INF = 0x3fffffff;
const int mod = 1000000007;
vector<int> G[maxn], rG[maxn]; // 原图G和它的反图
vector<int> S; // 存储第一次dfs的结果:标记点的先后顺序
int vis[maxn]; // 访问标记
int sccno[maxn]; // sccno[i]表示第i个点所属的强连通分量
int cnt; // 强连通分量的个数
int n, m;
void dfs1(int u) { // 在原图G上做一次dfs,标记点的先后顺序
S.push_back(u); // 记录点的先后顺序
vis[u] = true;
for (int i = 0; i < G[u].size(); i++) {
if (!vis[G[u][i]]) {
dfs1(G[u][i]);
}
}
}
void dfs2(int u) { // 在反图rG上做一次dfs,顺序从标记最大的点开始,到标记最小的点。
sccno[u] = cnt;
for (int i = 0; i < rG[u].size(); i++) {
if (!sccno[rG[u][i]]) {
dfs2(rG[u][i]);
}
}
}
void Kosaraju() {
cnt = 0;
S.clear();
memset(sccno, 0, sizeof sccno);
memset(vis, 0, sizeof vis);
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
dfs1(i);
}
}
for (int i = 0; i < n; i++) {
if (!sccno[S[i]]) {
cnt++;
dfs2(S[i]);
}
}
}
void solve() {
int u, v;
while (cin >> n >> m, n != 0 || m != 0) {
for (int i = 1; i <= n; i++) {
G[i].clear();
rG[i].clear();
}
for (int i = 0; i < m; i++) {
cin >> u >> v;
G[u].push_back(v); // 原图
rG[v].push_back(u); // 反图
}
Kosaraju();
cout << (cnt == 1 ? "Yes\n" : "No\n");
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(18);
solve();
return 0;
}#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e4 + 10;
const int INF = 0x3fffffff;
const int mod = 1000000007;
vector<int> G[maxn], rG[maxn]; // 原图G和它的反图
vector<int> S; // 存储第一次dfs的结果:标记点的先后顺序
int vis[maxn]; // 访问标记
int sccno[maxn]; // sccno[i]表示第i个点所属的强连通分量
int cnt; // 强连通分量的个数
int n, m;
void dfs1(int u) { // 在原图G上做一次dfs,标记点的先后顺序
vis[u] = true;
for (int i = 0; i < G[u].size(); i++) {
if (!vis[G[u][i]]) {
dfs1(G[u][i]);
}
}
S.push_back(u); // 记录点的先后顺序,标记大的放在S的后面
}
void dfs2(int u) { // 在反图rG上做一次dfs,顺序从标记最大的点开始,到标记最小的点。
sccno[u] = cnt;
for (int i = 0; i < rG[u].size(); i++) {
if (!sccno[rG[u][i]]) {
dfs2(rG[u][i]);
}
}
}
void Kosaraju() {
cnt = 0;
S.clear();
memset(sccno, 0, sizeof sccno);
memset(vis, 0, sizeof vis);
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
dfs1(i);
}
}
for (int i = n - 1; i >= 0; i--) {
if (!sccno[S[i]]) {
cnt++;
dfs2(S[i]);
}
}
}
void solve() {
int u, v;
while (cin >> n >> m, n != 0 || m != 0) {
for (int i = 1; i <= n; i++) {
G[i].clear();
rG[i].clear();
}
for (int i = 0; i < m; i++) {
cin >> u >> v;
G[u].push_back(v); // 原图
rG[v].push_back(u); // 反图
}
Kosaraju();
cout << (cnt == 1 ? "Yes\n" : "No\n");
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(18);
solve();
return 0;
}Tarjan算法:
算法原理及步骤:
在讲Tarjan算法之前,我们需要给出一个定理:一个SCC,从其中任意一点出发,都至少有一条路径可以回到自己。那么其实从任意一点开始DFS,这个点都会成为这个SCC的祖先。
我们可以在DFS求low值的同时把点按SCC(有相同的low值)分开,用栈分离不同的SCC。关于low值的定义可以看看我之前关于割点割边的随笔。
大体步骤:
dfn[u]表示dfs时达到顶点u的次序号(时间戳),low[u]表示以u为根节点的dfs树中次序号最小的顶点的次序号,所以当dfn[u]=low[u]时,以u为根的搜索子树上所有节点是一个强连通分量。 先将顶点u入栈,dfn[u]=low[u]=++idx,扫描u能到达的顶点v,如果v没有被访问过,则dfs(v),low[u]=min(low[u],low[v]),如果v在栈里,low[u]=min(low[u],dfn[v]),扫描完v以后,如果dfn[u]=low[u],则将u及其以上顶点出栈。
考虑最先入栈的点,每进入一个新的SCC,访问并入栈的第1个点都是这个SCC的祖先,它的num值和low值相等,这个SCC中所有的点的low值都与它相等。
参考代码:
例题仍然是hdu1269
#include <bits/stdc++.h>
using namespace std;
#define endl '\n'
typedef long long ll;
typedef unsigned long long ull;
const int maxn = 1e4 + 10;
const int INF = 0x3fffffff;
const int mod = 1000000007;
int num[maxn]; // 记录每个节点的dfs次序,时间戳
int low[maxn]; // low[v]表示v以及v的后代能退回到的节点的num值最小是多少
int sccno[maxn]; // sccno[u]表示u点属于哪个强连通分量
int st[maxn], top; // 模拟栈
vector<int> G[maxn]; // 图
int dfn; // dfs次序,时间戳
int cnt; // 强连通分量的个数
int n, m;
void dfs(int u) {
st[top++] = u; // u入栈
low[u] = num[u] = ++dfn;
for (int i = 0; i < G[u].size(); i++) {
int v = G[u][i];
if (!num[v]) { // 未访问过的点,继续dfs
dfs(v); // dfs的最底层,是最后一个SCC
low[u] = min(low[u], low[v]);
} else if (!sccno[v]) { // 处理回退边
low[u] = min(low[u], num[v]);
}
}
if (low[u] == num[u]) { // 栈底的点是SCC的祖先,它的low == num
cnt++;
while (1) {
int v = st[--top]; // v弹出栈
sccno[v] = cnt;
if (u == v) { // 栈底的点是SCC的祖先
break;
}
}
}
}
void tarjan() {
cnt = top = dfn = 0;
memset(sccno, 0, sizeof sccno);
memset(num, 0, sizeof num);
memset(low, 0, sizeof low);
for (int i = 1; i <= n; i++) {
if (!num[i]) {
dfs(i);
}
}
}
void solve() {
int u, v;
while (cin >> n >> m, n != 0 || m != 0) {
for (int i = 1; i <= n; i++) {
G[i].clear();
}
for (int i = 0; i < m; i++) {
cin >> u >> v;
G[u].push_back(v);
}
tarjan();
cout << (cnt == 1 ? "Yes\n" : "No\n");
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cout << fixed;
cout.precision(18);
solve();
return 0;
}




![[保研/考研机试] KY207 二叉排序树 清华大学复试上机题 C++实现](https://img-blog.csdnimg.cn/9aceff213b5d4973a7e73264b6517849.png)


