广义线性模型
考虑单点可微函数
g
(
⋅
)
g(\cdot)
g(⋅),令
y
=
g
−
1
(
ω
T
x
+
b
)
y=g^{-1}(\omega^{T}x+b)
y=g−1(ωTx+b),这样得到的模型称为“广义线性模型”,其中函数
g
(
⋅
)
g(\cdot)
g(⋅)称为“联系函数”。显然,对数线性回归是广义线性模型在
g
(
⋅
)
=
ln
(
⋅
)
g(\cdot)=\ln (\cdot)
g(⋅)=ln(⋅)时的特例。
对数几率回归
在线性回归模型的基础上,改进以完成分类任务。关键在于寻找一个单调可微函数,将分类任务的真实标记
y
y
y与线性回归模型的预测值联系起来。
考虑二分类任务
y
∈
{
0
,
1
}
⇔
z
=
ω
T
x
+
b
y\in \{0,1\}\Leftrightarrow z=\omega^Tx+b
y∈{0,1}⇔z=ωTx+b
于是,我们需将实值z转换为0/1值。
- 单位跃阶函数:
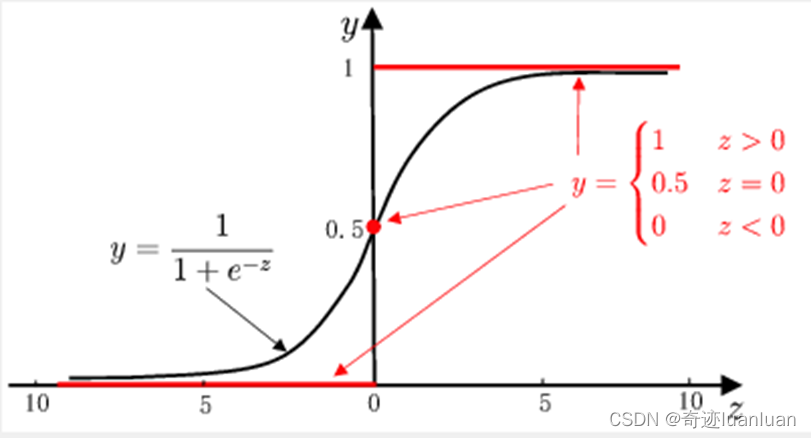
y = { 0 , z < 0 0.5 , z = 0 1 , z > 0 y= \left\{ \begin{aligned} 0,\quad z<0\\ 0.5,\quad z=0\\ 1,\quad z>0 \end{aligned} \right. y=⎩ ⎨ ⎧0,z<00.5,z=01,z>0
单位跃阶函数不连续,从而不可微,故不能直接作为联系函数。 - 对数几率函数
y = 1 1 + e − z y=\frac{1}{1+e^{-z}} y=1+e−z1
对数几率函数是一种Sigmoid函数。
Sigmoid函数即形似S的函数,对率函数是Sigmoid函数最重要代表。
代入广义线性模型中得到
y
=
1
1
+
e
−
(
ω
T
x
+
b
)
=
e
ω
T
x
+
b
1
+
e
ω
T
x
+
b
1
−
y
=
e
−
(
ω
T
x
+
b
)
1
+
e
−
(
ω
T
x
+
b
)
=
1
1
+
e
ω
T
x
+
b
y
1
−
y
=
e
ω
T
x
+
b
ln
y
1
−
y
=
ω
T
x
+
b
\begin{aligned} &y=\frac{1}{1+e^{-(\omega^{T}x+b)}}=\frac{e^{\omega^Tx+b}}{1+e^{\omega^Tx+b}} \\ &1-y=\frac{e^{-(\omega^Tx+b)}}{1+e^{-(\omega^Tx+b)}}=\frac{1}{1+e^{\omega^Tx+b}}\\ &\frac{y}{1-y}=e^{\omega^Tx+b}\\ &\ln \frac{y}{1-y}=\omega^Tx+b \end{aligned}
y=1+e−(ωTx+b)1=1+eωTx+beωTx+b1−y=1+e−(ωTx+b)e−(ωTx+b)=1+eωTx+b11−yy=eωTx+bln1−yy=ωTx+b
若将y视为样本x作为正例的可能性,则1-y为样本x为反例的可能性,两者的比值
y
1
−
y
\frac{y}{1-y}
1−yy称为“几率”,反映了样本x作为正例的可能性。对几率取对数则得到“对数几率”:
ln
y
1
−
y
\ln \frac{y}{1-y}
ln1−yy。
l
n
y
1
−
y
=
ω
T
x
+
b
ln \frac{y}{1-y}=\omega^Tx+b
ln1−yy=ωTx+b
实际上是用线性回归模型的预测结果去逼近真实的对数几率,因此该模型也称为“对数几率回归”。(虽然名字叫做回归,但实际上是一种分类学习方法)
对数几率回归的优点
- 它是直接对分类的可能性进行建模,无需事先假设数据的分布,这样就避免了假设分布不准确所带来的问题。
- 它不仅预能预测出类别,而是可以得到近似概率预测,这对许多需要利用概率辅助决策的任务很有用。
- 对率函数是任意阶可导的凸函数,有很好的数学性质,现有的很多数值优化算法都可以直接用于求取最优解。
求解对率回归模型中的参数
将y视为类后验概率估计
p
(
y
=
1
∣
x
)
p(y=1|x)
p(y=1∣x),则对率函数可重写为
ln
p
(
y
=
1
∣
x
)
p
(
y
=
0
∣
x
)
=
ω
T
x
+
b
\ln \frac{p(y=1|x)}{p(y=0|x)}=\omega^Tx+b
lnp(y=0∣x)p(y=1∣x)=ωTx+b
由于
p
(
y
=
1
∣
x
)
+
p
(
y
=
0
∣
x
)
=
1
p(y=1|x)+p(y=0|x)=1
p(y=1∣x)+p(y=0∣x)=1,从而有
y
=
p
(
y
=
1
∣
x
)
=
e
ω
T
x
+
b
1
+
e
ω
T
x
+
b
1
−
y
=
p
(
y
=
0
∣
x
)
=
1
1
+
e
ω
T
x
+
b
\begin{aligned} y=p(y=1|x)=\frac{e^{\omega^Tx+b}}{1+e^{\omega^Tx+b}} \\ 1-y=p(y=0|x)=\frac{1}{1+e^{\omega^Tx+b}} \end{aligned}
y=p(y=1∣x)=1+eωTx+beωTx+b1−y=p(y=0∣x)=1+eωTx+b1于是可以通过极大似然法来估计
ω
\omega
ω和
b
b
b。给定数据集
{
(
x
i
,
y
i
)
}
i
=
1
m
\{(x_i,y_i)\}_{i=1}^m
{(xi,yi)}i=1m,对率回归模型最大化“对数似然”
l
(
ω
;
b
)
=
∑
i
=
1
m
ln
p
(
y
i
∣
x
i
;
ω
,
b
)
l(\omega;b)=\sum_{i=1}^m{\ln p(y_i|x_i;\omega,b)}
l(ω;b)=i=1∑mlnp(yi∣xi;ω,b)即令每个样本属于其真实标记的概率越大越好。为了便于讨论,令
β
=
(
ω
;
b
)
,
x
^
=
(
x
;
1
)
\beta=(\omega;b),\quad \hat{x}=(x;1)
β=(ω;b),x^=(x;1),则
ω
T
x
+
b
\omega^Tx+b
ωTx+b可以简写为
β
T
x
^
\beta^T\hat{x}
βTx^。再令
p
1
(
x
^
;
β
)
=
p
(
y
=
1
∣
x
^
;
β
)
,
p
0
(
x
^
;
β
)
=
p
(
y
=
0
∣
x
^
;
β
)
=
1
−
p
1
(
x
^
;
β
)
p_1(\hat{x};\beta)=p(y=1|\hat{x};\beta),p_0(\hat{x};\beta)=p(y=0|\hat{x};\beta)=1-p_1(\hat{x};\beta)
p1(x^;β)=p(y=1∣x^;β),p0(x^;β)=p(y=0∣x^;β)=1−p1(x^;β),则上式中的似然项可重写为
p
(
y
i
∣
x
i
;
ω
,
b
)
=
y
i
p
1
(
x
^
i
;
β
)
+
(
1
−
y
i
)
p
0
(
x
^
i
;
β
)
p(y_i|x_i;\omega,b)=y_ip_1(\hat{x}_i;\beta)+(1-y_i)p_0(\hat{x}_i;\beta)
p(yi∣xi;ω,b)=yip1(x^i;β)+(1−yi)p0(x^i;β),进一步代入得
l
(
ω
;
b
)
=
∑
i
=
1
m
ln
[
y
i
p
1
(
x
^
i
;
β
)
+
(
1
−
y
i
)
p
0
(
x
^
i
;
β
)
]
=
∑
i
=
1
m
ln
[
y
i
e
ω
T
x
i
+
b
1
+
e
ω
T
x
i
+
b
+
(
1
−
y
i
)
1
1
+
e
ω
T
x
i
+
b
]
=
∑
i
=
1
m
ln
[
y
i
e
β
T
x
^
i
1
+
e
β
T
x
^
i
+
(
1
−
y
i
)
1
1
+
e
β
T
x
^
i
]
=
∑
i
=
1
m
ln
[
y
i
e
β
T
x
^
i
−
y
i
+
1
1
+
e
β
T
x
^
i
]
=
∑
i
=
1
m
[
ln
(
y
i
e
β
T
x
^
i
−
y
i
+
1
)
−
ln
(
1
+
e
β
T
x
^
i
)
]
=
∑
y
i
=
0
−
ln
(
1
+
e
β
T
x
^
i
)
+
∑
y
i
=
1
[
ln
(
e
β
T
x
^
i
)
−
ln
(
1
+
e
β
T
x
^
i
)
]
=
−
∑
y
i
=
0
ln
(
1
+
e
β
T
x
^
i
)
+
∑
y
i
=
1
[
β
T
x
^
i
−
ln
(
1
+
e
β
T
x
^
i
)
]
=
∑
i
=
1
m
[
y
i
β
T
x
^
i
−
ln
(
1
+
e
β
T
x
^
i
)
]
\begin{aligned} l(\omega;b)&=\sum_{i=1}^m{\ln \left[ y_ip_1(\hat{x}_i;\beta)+(1-y_i)p_0(\hat{x}_i;\beta)\right]}\\ &=\sum_{i=1}^m{\ln \left[y_i\frac{e^{\omega^Tx_i+b}}{1+e^{\omega^Tx_i+b}}+(1-y_i)\frac{1}{1+e^{\omega^Tx_i+b}}\right]}\\ &=\sum_{i=1}^m{\ln \left[y_i\frac{e^{\beta^T\hat{x}_i}}{1+e^{\beta^T\hat{x}_i}}+(1-y_i)\frac{1}{1+e^{\beta^T\hat{x}_i}}\right]}\\ &=\sum_{i=1}^m{\ln \left[\frac{y_ie^{\beta^T\hat{x}_i}-y_i+1}{1+e^{\beta^T\hat{x}_i}}\right]}\\ &=\sum_{i=1}^m{\left[\ln (y_ie^{\beta^T\hat{x}_i}-y_i+1)-\ln (1+e^{\beta^T\hat{x}_i})\right]}\\ &=\sum_{y_i=0}{-\ln (1+e^{\beta^T\hat{x}_i})}+\sum_{y_i=1}{\left[\ln(e^{\beta^T\hat{x}_i})-\ln(1+e^{\beta^T\hat{x}_i})\right]}\\ &=-\sum_{y_i=0}{\ln (1+e^{\beta^T\hat{x}_i})}+\sum_{y_i=1}{\left[\beta^T\hat{x}_i-\ln(1+e^{\beta^T\hat{x}_i})\right]}\\ &=\sum_{i=1}^m{\left[y_i\beta^T\hat{x}_i-\ln(1+e^{\beta^T\hat{x}_i})\right]} \end{aligned}
l(ω;b)=i=1∑mln[yip1(x^i;β)+(1−yi)p0(x^i;β)]=i=1∑mln[yi1+eωTxi+beωTxi+b+(1−yi)1+eωTxi+b1]=i=1∑mln[yi1+eβTx^ieβTx^i+(1−yi)1+eβTx^i1]=i=1∑mln[1+eβTx^iyieβTx^i−yi+1]=i=1∑m[ln(yieβTx^i−yi+1)−ln(1+eβTx^i)]=yi=0∑−ln(1+eβTx^i)+yi=1∑[ln(eβTx^i)−ln(1+eβTx^i)]=−yi=0∑ln(1+eβTx^i)+yi=1∑[βTx^i−ln(1+eβTx^i)]=i=1∑m[yiβTx^i−ln(1+eβTx^i)]
从而最大化
l
(
ω
;
b
)
l(\omega;b)
l(ω;b)等价于最小化
l
(
β
)
=
∑
i
=
1
m
(
−
y
i
β
T
x
^
i
+
ln
(
1
+
e
β
T
x
^
i
)
)
l(\beta)=\sum_{i=1}^m{\left(-y_i\beta^T\hat{x}_i+\ln(1+e^{\beta^T\hat{x}_i})\right)}
l(β)=i=1∑m(−yiβTx^i+ln(1+eβTx^i))
l
(
β
)
l(\beta)
l(β)是关于
β
\beta
β的高阶可导函数,根据凸优化理论,经典的数值优化方法如梯度下降法、牛顿法等都可求得其最优解,于是就得到
β
∗
=
a
r
g
m
i
n
β
l
(
β
)
\beta^*=argmin_{\beta}l(\beta)
β∗=argminβl(β)
例如牛顿法,其第t+1次轮迭代解的更新公式为
β
t
+
1
=
β
t
−
(
∂
2
l
(
β
)
∂
β
∂
β
T
)
−
1
∂
l
(
β
)
∂
β
\beta^{t+1}=\beta^{t}-{\left(\frac{\partial^2l(\beta)}{\partial\beta\partial\beta^T}\right)^{-1}\frac{\partial l(\beta)}{\partial\beta}}
βt+1=βt−(∂β∂βT∂2l(β))−1∂β∂l(β)
其中关于
β
\beta
β的一阶、二阶导数分别为
∂
l
(
β
)
∂
β
=
−
∑
i
=
1
m
x
^
i
(
y
i
−
p
1
(
x
^
i
;
β
)
)
∂
2
l
(
β
)
∂
β
∂
β
T
=
∑
i
=
1
m
x
^
i
x
^
i
T
p
1
(
x
^
i
;
β
)
(
1
−
p
1
(
x
^
i
;
β
)
)
\begin{aligned} \frac{\partial l(\beta)}{\partial \beta}&=-\sum_{i=1}^m{\hat{x}_i(y_i-p_1(\hat{x}_i;\beta))}\\ \frac{\partial^2l(\beta)}{\partial\beta\partial\beta^T}&=\sum_{i=1}^m{\hat{x}_i\hat{x}_i^Tp_1(\hat{x}_i;\beta)(1-p_1(\hat{x}_i;\beta))} \end{aligned}
∂β∂l(β)∂β∂βT∂2l(β)=−i=1∑mx^i(yi−p1(x^i;β))=i=1∑mx^ix^iTp1(x^i;β)(1−p1(x^i;β))
【小试牛刀】
编程实现对率回归,并给出西瓜数据集3.0a上的结果。
import numpy as np
import pandas as pd
import xlrd
#第一步导入数据
DataSet=pd.read_excel("西瓜数据集3.0a.xlsx")
Data=DataSet.values
#print(Data.shape) #17行4列
X=np.delete(Data,0,1)#在Data的copy基础上删除第一列编号
X=np.delete(X,2,1)
#print(X)
y=Data[:,3]
#print(y)#仍然是ndarray
#利用牛顿法求解
def calp1(x,Beta):
"""
求解样本x在参数beta下取正例的概率p1
此处Beta为列向量(3,1),x为列向量(3,1)
"""
temp=np.exp(np.dot(x.T,Beta))
p1=temp/float(1+temp)
return p1
def calpartial1(X_hat,y,beta):
"""
求解l(beta)关于参数beta的一阶导数
X_hat[i]是行向量,每一行代表一个样本
"""
m=len(y)
partial1=0
for i in range(m):
x_hat=X_hat[i].reshape(3,1)#把样本x变为列矩阵
temp=np.dot(x_hat,y[i]-calp1(x_hat,beta))
partial1=partial1+temp
return -partial1
def calpartial2(X_hat,y,beta):
"""
求解l(beta)关于beta的二阶导数
beta为列向量
"""
m=len(y)
partial2=0
for i in range(m):
x_hat=X_hat[i].reshape(3,1)#把样本x变为列矩阵
xxT=np.dot(x_hat,x_hat.T)
p1=calp1(x_hat,beta)
temp=p1*(1-p1)*xxT
partial2+=temp
return partial2
def LR(X,y,beta,error):
"""
error为误差
"""
#在数据集X(每行为一个样本)添加一列1
#方法一
X_hat=np.insert(X,2,values=1,axis=1)
"""
col=np.ones((17,1))#创建一个17行1列的元素全为1的二维数组
Z=np.c_[X,col]
print(Z)
"""
t=0#迭代次数
while t<10000:
beta1=beta-np.linalg.inv(calpartial2(X_hat,y,beta)).dot(calpartial1(X_hat,y,beta))
if np.linalg.norm(beta-beta1,2)<error:
return beta1
else:
t=t+1
beta=beta1
print("超过最大迭代次数,认为不收敛!")
np.random.seed(1)
beta=np.random.rand(3,1)
Beta=LR(X,y,beta,1e-5)
print(Beta)
输出:

【编程中注意的一些问题】
- DataSet是Pandas内的对象,决策树的构建需要用到scikit-learn。
Pandas和Scikit-learn没有完美整合,而Numpy和scikit-learn能够很好的协同使用。
从而现将Pandas中的值转化为Numpy,然后再配合scikit-learn工作
numpy中的ndarray为多维数组,是numpy中最为重要也是python进行科学计算非常重要和基本的数据类型。 - numpy矩阵运算大全见这篇博客
numpy中文官网:https://www.numpy.org.cn/reference/
numpy英文官网:https://numpy.org/doc/stable/index.html/
特别注意矩阵乘法:ndarray 是 NumPy 的基础元素,NumPy 又主要是用来进行矩阵运算的.首先,在矩阵用 ±*/ 这些常规操作符操作的时候,是对元素进行操作。这和其他诸如 MATLAB 等语言不一样。 ∗ * ∗并没有进行矩阵乘法,而是矩阵和矩阵的元素进行了相乘。想要进行矩阵乘法计算,需要用dot方法
- numpy.dot()用法:
- numpy.dot()如果处理的是一维数组,则代表向量点积,并且结果与两个参数的位置顺序无关
a1=np.array([1,2,3])
b1=np.array([2,2,2])
print(a1.shape,b1.shape)#(3,) (3,)
print(np.dot(a1,b1),np.dot(b1,a1))#12 12
- numpy.dot()如果处理的是二维数组(矩阵),则代表矩阵乘法
a2=np.arange(3,6,1).reshape(1,3)
print(a2,a2.shape)#[[3,4,5]] (1,3)
b2=np.array([[2,4,6]])
print(b2.shape)#(1,3)
#print(np.dot(b2,a2))#报错
c2=b2.reshape(3,1)
print(c2,c2.shape)
"""
[[2]
[4]
[6]] (3,1)
"""
print(np.dot(c2,a2),np.dot(a2,c2))
"""
[[ 6 8 10]
[12 16 20]
[18 24 30]] [[52]]
"""
- 标量p与二维数组A相乘时,直接使用p*A
- 向量与二维数组做运算时,不能直接使用numpy.dot()
#解决(3,1)和(3,)在做矩阵积的时候维度不匹配的问题
np.random.seed(1)
a=np.random.randint(1,10,size=(3,1))
print(a.shape)
b=np.append(X[5],[1],0)
print(b)
c=b.reshape(1,3)
print(c)
print(np.dot(a,c))
线性判别分析
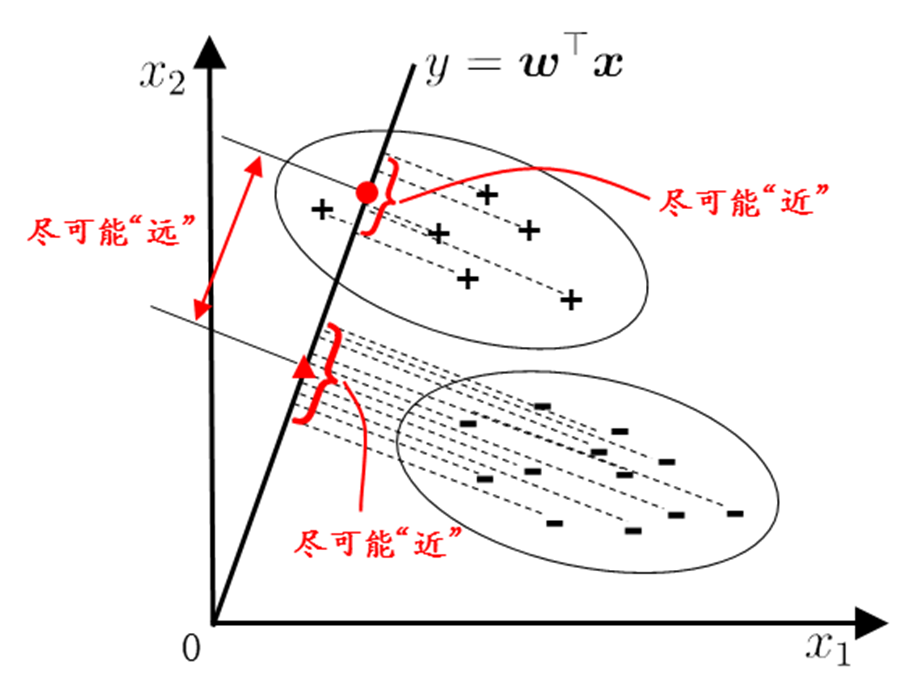
线性判别的思想非常朴素:给定训练样例集,设法将样例投影到一条直线上,使得同类样例的投影点尽可能接近,异样样例的投影点尽可能远离;在对新样本进行分类时,将其投影到同样的直线上,再根据投影点的位置来确定新样本的类别。
理论推导过程:
数据集: D = { ( x i , y i ) } i = 1 m , y i ∈ { 0 , 1 } , x i ∈ R d D=\{(x_i,y_i)\}_{i=1}^m,y_i\in\{0,1\},x_i\in R^d D={(xi,yi)}i=1m,yi∈{0,1},xi∈Rd
X 0 = { x i ∣ y i = 0 } , X 1 = { x i ∣ y i = 1 } X_0=\{x_i|y_i=0\},X_1=\{x_i|y_i=1\} X0={xi∣yi=0},X1={xi∣yi=1}
设
X
i
(
i
=
0
,
1
)
X_i(i=0,1)
Xi(i=0,1)中的样例数量为
n
i
,
n
0
+
n
1
=
m
n_i,n_0+n_1=m
ni,n0+n1=m,均值向量为
μ
i
=
∑
x
∈
X
i
x
\mu_i=\sum_{x\in X_i}x
μi=∑x∈Xix,协方差矩阵
Σ
i
=
1
n
i
∑
x
j
∈
X
i
(
x
j
−
μ
i
)
(
x
j
−
μ
i
)
T
\Sigma_i=\frac{1}{n_i}\sum_{x_j\in X_i}{(x_j-\mu_i)(x_j-\mu_i)^T}
Σi=ni1∑xj∈Xi(xj−μi)(xj−μi)T
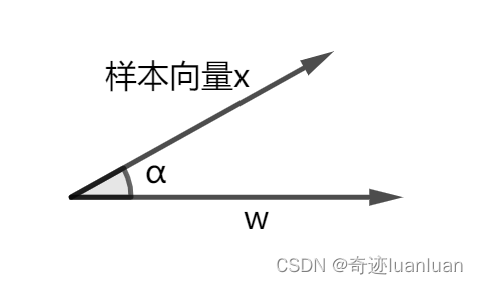
向量x在向量w上的投影
a
(
a
∈
R
)
a(a\in R)
a(a∈R):
a
=
∣
x
∣
c
o
s
α
=
∣
ω
∣
∣
x
∣
c
o
s
α
∣
o
m
e
g
a
∣
=
ω
T
x
∣
ω
∣
a=|x|cos\alpha=\frac{|\omega||x|cos\alpha}{|omega|}=\frac{\omega^Tx}{|\omega|}
a=∣x∣cosα=∣omega∣∣ω∣∣x∣cosα=∣ω∣ωTx
则对应的投影向量为
a
ω
∣
ω
∣
=
ω
T
x
∣
ω
∣
ω
∣
ω
∣
=
ω
T
x
ω
ω
T
ω
a\frac{\omega}{|\omega|}=\frac{\omega^Tx}{|\omega|}\frac{\omega}{|\omega|}=\frac{\omega^Tx\omega}{\omega^T\omega}
a∣ω∣ω=∣ω∣ωTx∣ω∣ω=ωTωωTxω
容易证明,
X
i
X_i
Xi中样例在
ω
\omega
ω上投影的均值=
X
i
X_i
Xi中样例的均值向量在
ω
\omega
ω上的投影,即
1
n
i
∑
x
j
∈
X
i
ω
T
x
j
=
ω
T
(
1
n
i
∑
x
j
∈
X
i
x
j
)
=
ω
T
μ
i
\frac{1}{n_i}\sum_{x_j\in X_i}\omega^Tx_j=\omega^T(\frac{1}{n_i}\sum_{x_j\in X_i}x_j)=\omega^T\mu_i
ni1∑xj∈XiωTxj=ωT(ni1∑xj∈Xixj)=ωTμi
从而将两类样本投影到向量
ω
\omega
ω上,则两类样本投影点的中心分别为
ω
T
μ
0
(
μ
0
T
ω
)
\omega^T\mu_0(\mu_0^T\omega)
ωTμ0(μ0Tω)和
ω
T
μ
1
(
μ
1
T
ω
)
\omega^T\mu_1(\mu_1^T\omega)
ωTμ1(μ1Tω)
两类样本点投影的协方差分别为
X
0
:
1
n
0
∑
x
j
∈
X
0
(
ω
T
x
j
−
ω
T
μ
0
)
(
ω
T
x
j
−
ω
T
μ
0
)
T
【协方差的计算公式之一】
=
1
n
0
∑
x
j
∈
X
0
ω
T
(
x
i
−
μ
0
)
(
x
i
−
μ
0
)
T
ω
=
ω
T
(
1
n
0
∑
x
j
∈
X
0
(
x
i
−
μ
0
)
(
x
i
−
μ
0
)
T
)
ω
=
ω
T
Σ
0
ω
X
1
:
ω
T
Σ
1
ω
【同理】
\begin{aligned} X_0&:\frac{1}{n_0}\sum_{x_j\in X_0}{(\omega^Tx_j-\omega^T\mu_0)(\omega^Tx_j-\omega^T\mu_0)^T}【协方差的计算公式之一】\\ &=\frac{1}{n_0}\sum_{x_j\in X_0}{\omega^T(x_i-\mu_0)(x_i-\mu_0)^T\omega}\\ &=\omega^T\left(\frac{1}{n_0}\sum_{x_j\in X_0}{(x_i-\mu_0)(x_i-\mu_0)^T}\right)\omega\\ &=\omega^T\Sigma_0\omega\\ X_1&:\omega^T\Sigma_1\omega【同理】 \end{aligned}
X0X1:n01xj∈X0∑(ωTxj−ωTμ0)(ωTxj−ωTμ0)T【协方差的计算公式之一】=n01xj∈X0∑ωT(xi−μ0)(xi−μ0)Tω=ωT
n01xj∈X0∑(xi−μ0)(xi−μ0)T
ω=ωTΣ0ω:ωTΣ1ω【同理】
欲使同类样本点的投影点尽可能接近,可以让同类样例投影点的协方差尽可能小,即
ω
T
Σ
0
ω
+
ω
T
Σ
1
ω
\omega^T\Sigma_0\omega+\omega^T\Sigma_1\omega
ωTΣ0ω+ωTΣ1ω尽可能小;欲使异类样本的投影点尽可能远离,可以让异类样本点投影后的中心之间的距离尽可能的大,即
∣
∣
ω
T
μ
0
−
ω
T
μ
1
∣
∣
2
2
{||\omega^T\mu_0-\omega^T\mu_1||}_2^2
∣∣ωTμ0−ωTμ1∣∣22尽可能大。 同时考虑二者,可以得到优化目标:
J
(
ω
)
=
∣
∣
ω
T
μ
0
−
ω
T
μ
1
∣
∣
2
2
ω
T
Σ
0
ω
+
ω
T
Σ
1
ω
=
ω
T
(
μ
0
−
μ
1
)
(
μ
0
−
μ
1
)
T
ω
ω
T
(
Σ
0
+
Σ
1
)
ω
\begin{aligned} J(\omega)&=\frac{{||\omega^T\mu_0-\omega^T\mu_1||}_2^2}{\omega^T\Sigma_0\omega+\omega^T\Sigma_1\omega}\\ &=\frac{\omega^T(\mu_0-\mu_1)(\mu_0-\mu_1)^T\omega}{\omega^T(\Sigma_0+\Sigma_1)\omega} \end{aligned}
J(ω)=ωTΣ0ω+ωTΣ1ω∣∣ωTμ0−ωTμ1∣∣22=ωT(Σ0+Σ1)ωωT(μ0−μ1)(μ0−μ1)Tω
定义类内散度矩阵
S
ω
S_{\omega}
Sω(与
ω
\omega
ω无关)
S
ω
=
Σ
0
+
Σ
1
S_{\omega}=\Sigma_0+\Sigma_1
Sω=Σ0+Σ1
类间散度矩阵
S
b
S_b
Sb(与
ω
\omega
ω无关)
S
b
=
(
μ
0
−
μ
1
)
(
μ
0
−
μ
1
)
T
S_b=(\mu_0-\mu_1)(\mu_0-\mu_1)^T
Sb=(μ0−μ1)(μ0−μ1)T
此时优化目标可重写为
J
(
ω
)
=
ω
T
S
b
ω
ω
T
S
ω
ω
J(\omega)=\frac{\omega^TS_b\omega}{\omega^TS_{\omega}\omega}
J(ω)=ωTSωωωTSbω,即
S
b
S_b
Sb与
S
ω
S_{\omega}
Sω的“广义瑞利商”。
ω
\omega
ω的确定:
分子分母都是关于
ω
\omega
ω的二次项,因此J与
ω
\omega
ω的长度无关
J
(
ω
)
=
(
ω
∣
ω
∣
)
T
S
b
(
ω
∣
ω
∣
)
(
ω
∣
ω
∣
)
T
S
ω
(
ω
∣
ω
∣
)
J(\omega)=\frac{\left(\frac{\omega}{|\omega|}\right)^TS_b\left(\frac{\omega}{|\omega|}\right)}{\left(\frac{\omega}{|\omega|}\right)^TS_{\omega}\left(\frac{\omega}{|\omega|}\right)}
J(ω)=(∣ω∣ω)TSω(∣ω∣ω)(∣ω∣ω)TSb(∣ω∣ω),只与
ω
\omega
ω的方向有关。不是一般性,令
ω
T
S
ω
ω
=
1
\omega^TS_{\omega}\omega=1
ωTSωω=1,则LDA的优化目标等价于
m
i
n
ω
−
ω
T
S
b
ω
s
.
t
.
ω
T
S
ω
ω
=
1
\begin{aligned} min_{\omega}\quad -\omega^TS_b\omega\\ s.t.\quad \omega^TS_{\omega}\omega=1 \end{aligned}
minω−ωTSbωs.t.ωTSωω=1


![[保研/考研机试] KY207 二叉排序树 清华大学复试上机题 C++实现](https://img-blog.csdnimg.cn/9aceff213b5d4973a7e73264b6517849.png)