直方图是根据灰图像绘制的，而不是彩色图像通。查看图像直方图时候，需要先确定图片是否为灰度图，使用MATLAB2019查看图片是否是灰度图片，在读取图片后在MATLAB界面的工作区会显示读取的图像矩阵，如果是，那么该图片是灰度图像，如果是，那么该图片是彩色图像。

通过直方图可以对整幅图像的灰度分布有一个整体的了解：直方图的横轴是灰度级（0 到 255），纵轴是图片中具有同一个灰度值的点的数目。

在MATLAB中，可使用imhist函数来绘制灰度直方图，示例程序如下图所示。

%绘制灰度直方图

I = imread('rice.png') ;

subplot(1,2,1),imshow(I);     %在一个窗口中显示两幅图像，第一幅显示图像I

subplot(1,2,2),imhist(I);      %第二幅显示图像I的灰度直方图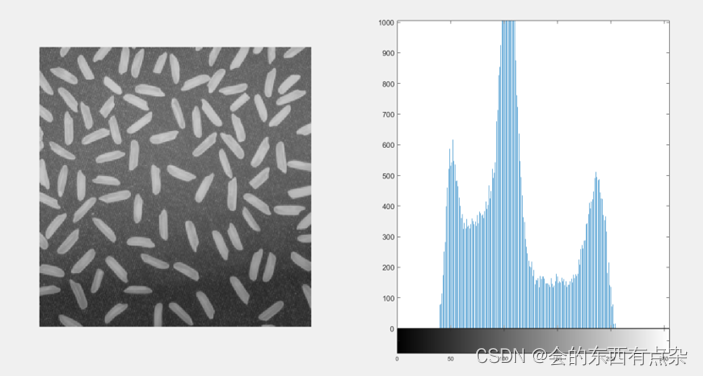

直方图的左边区域像是暗一点的像素数量，右侧显示了亮一点的像素的数量。从这幅图上你可以看到大米为亮一点的像素，背景颜色下方比上方更暗，所以这副图像的直方图波峰大致有三个：直方图左侧波峰为图像背景底部暗像素灰度，直方图中间波峰代表的是图像背景由中部至上部的稍微偏亮的暗像素灰度，直方图右侧波峰为图像中大米的亮像素灰度。

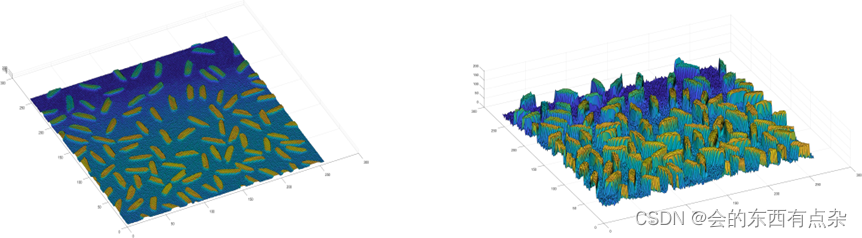
实际工作中，也可以利用三维直方图来综合反映图像灰度分布和邻域空间相关信息。以及灰度图像各分量间的关系。二维直方图实质上是一个二维数组 (三维矩阵 )。表示的是有 二个特征分量象索的分布频度。如下图所示

绘制三维直方图
I = imread('rice.png') ;
surf(I);           %绘制三维直方图