学习目标：对角线遍历算法

• 每日初级算法：对角线遍历

---

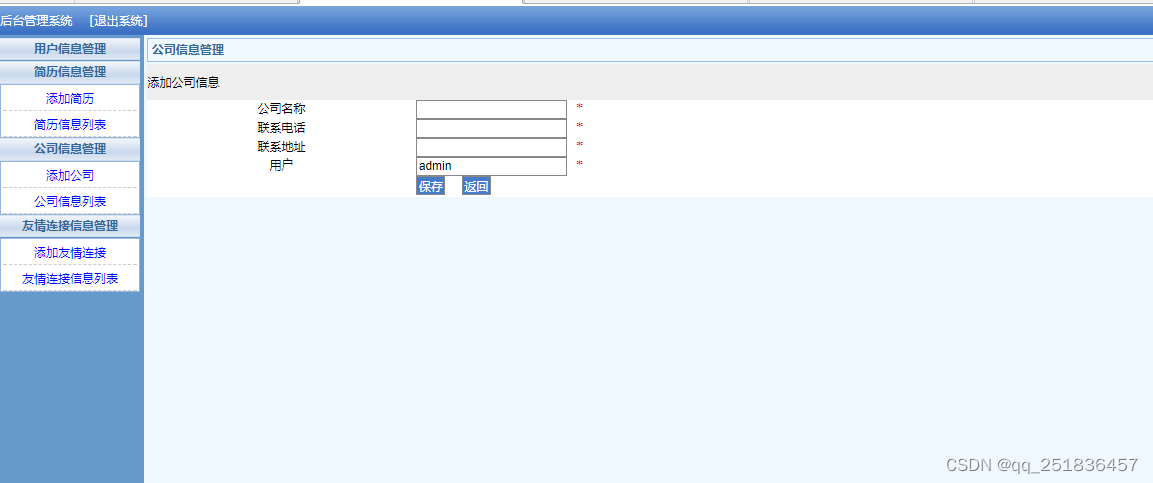
算法要求

给你一个大小为 m x n 的矩阵 mat ，请以对角线遍历的顺序，用一个数组返回这个矩阵中的所有元素

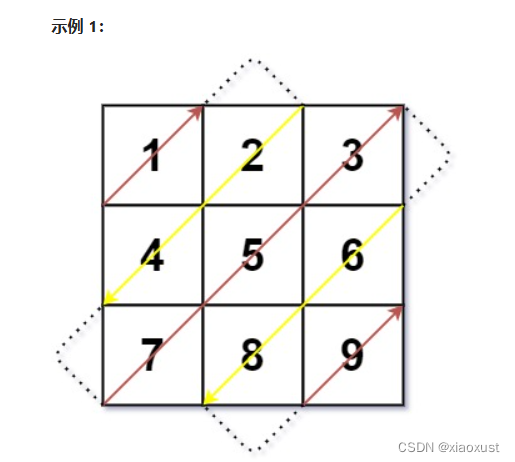
示例二：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,4,7,5,3,6,8,9]

示例三：

输入：mat = [[1,2],[3,4]]
输出：[1,2,3,4]

---

算法思路

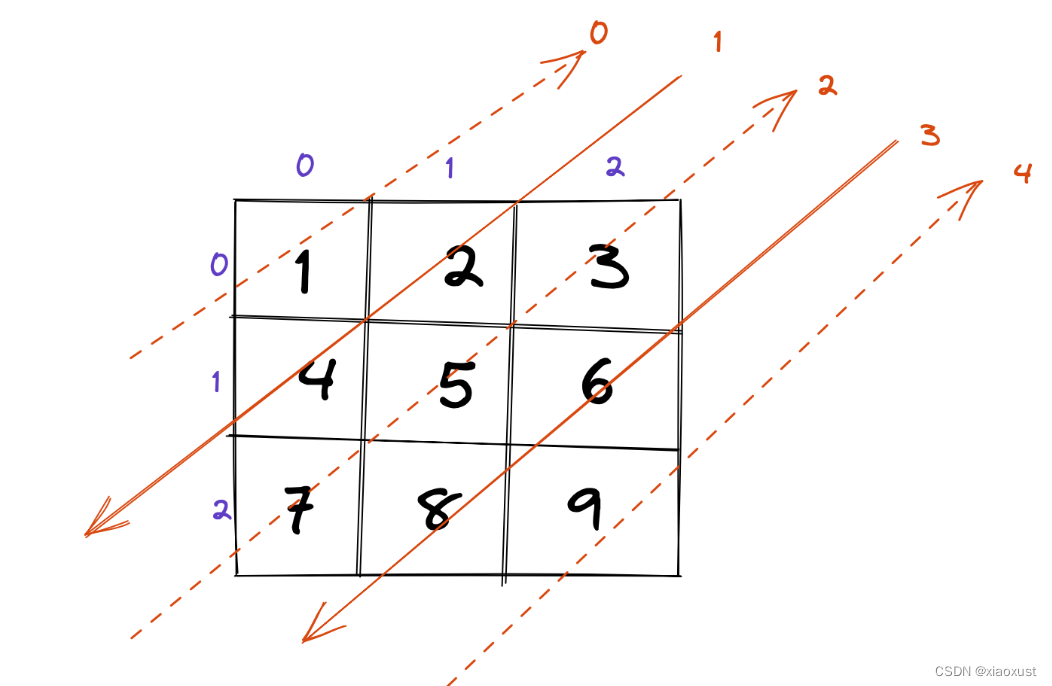
1. 对角线遍历，如图我们是33矩阵，可以看出对角线是5条，如果是22的就是3条，4*4的就是7条，可以得出结论，对角线的条数是 i=n+m-1条，所以便利条件就是 i<n+m-1。
2. 如图，对家线上面的每个元素的坐标和为该对角线的第几条数，如(2,1),(1,2)所在对角线为3，所以得出元素的坐标x,y与i的关系为:x+y = i。
3. 遍历方法：只要我们确定好遍历的起点和终点就好了，通过观察，我们发现，当i为偶数时，对角线从上往下遍历，当i为奇数时，对角线从下往上遍历。
   • 我们发现i为偶数时，当i=0时，他的起始位置跟终止位置都是0，所以i<n-1时，起始坐标为x=i,终止坐标为x=0
   • 当偶数为2时，我们发现起始坐标为（2，0），种植坐标为（0，2），我们得出结论，当i>=n-1时，起始点坐标x=n-1，终止点的坐标为y = m-1，根据1，2中的关系得出，x=i-(m-1)。
   • 所以偶数对角线遍历时起止点的x坐标为min(i,i-1)，结束点的x坐标为max(0,i-(m-1))，而坐标y就是i-x

---

算法实现

class Solution {
    public int[] findDiagonalOrder(int[][] mat) {
        int row = mat.length;
        int col = mat[0].length;
        //结果集
        int[] result = new int[row*col];
        int id = 0;
        for (int i = 0;i<row+col-1;i++){
            //奇数 从上往下遍历 x+1 y-1 起点:(0,1),(0,2),(1,2)
            if (i%2==1){
               int x = i<col?0:i-col+1;
               int y = i<col?i:col-1;
               while(x<row && y>=0) {
                   result[id] = mat[x][y];
                   id++;
                   x++;
                   y--;
               }
            }
            //偶数，从下往上遍历 x-1,y+1。起点:(0,0),(2,0),(2,1)
            if (i%2==0){
                int x = i<row?i:row-1;
                int y = i<row?0:i-row+1;
                while(x>=0 && y<col){
                    result[id] = mat[x][y];
                    id++;
                    x--;
                    y++;
                }
            }
        }
        return result;
    }
}