在这里插入图片描述

阅读导航

前言
一、priority_queue简介
- 1. 概念
- 2. 特点
二、priority_queue使用
- 1. 基本操作
- 2. 底层结构
三、priority_queue模拟实现
- ⭕ C++代码
- ⭕priority_queue中的仿函数
总结
温馨提示

前言

⭕文章绑定了VS平台下std::priority_queue的源码，大家可以下载了解一下😍

前面我们讲了C语言的基础知识，也了解了一些数据结构，并且讲了有关C++的命名空间的一些知识点以及关于C++的缺省参数、函数重载，引用和内联函数也认识了什么是类和对象以及怎么去new一个 ‘对象’ ，以及学习了几个STL的结构也相信大家都掌握的不错，接下来博主将会带领大家继续学习有关C++比较重要的知识点—— priority_queue（STL）优先队列。下面话不多说坐稳扶好咱们要开车了😍

一、priority_queue简介

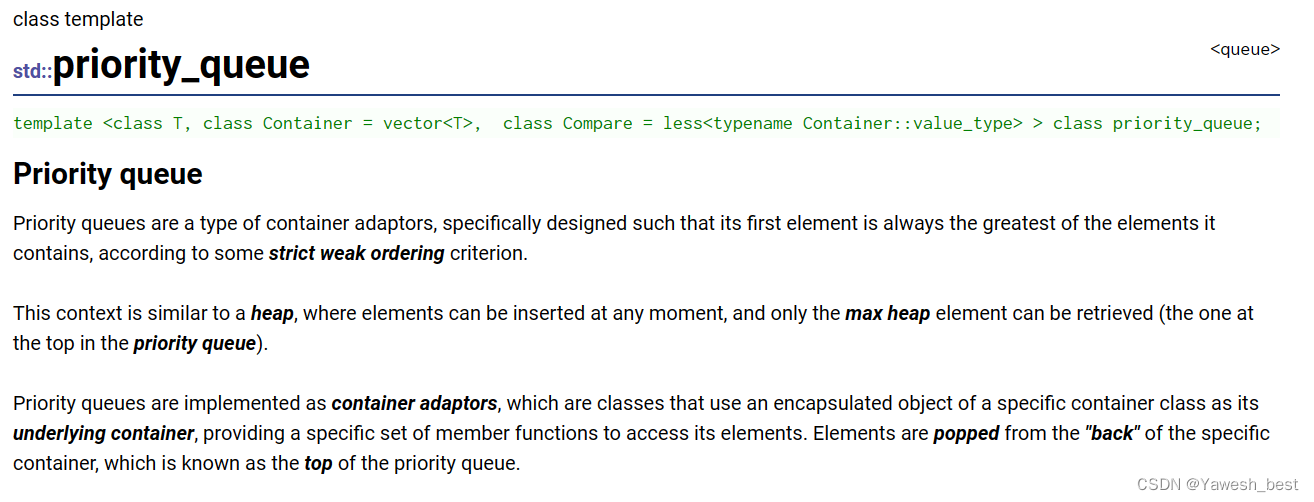
⭕官方文档
在这里插入图片描述

1. 概念

priority_queue是C++标准库中的一个容器适配器（container adapter），用于实现优先队列（priority queue）的数据结构。优先队列是一种特殊的队列，其中的元素按照一定的优先级进行排序，每次取出的元素都是优先级最高的。它的底层实现通常使用堆（heap）数据结构。

在C++中，priority_queue模板类定义在<queue>头文件中，可以通过指定元素类型和比较函数来创建不同类型的优先队列。比较函数用于确定元素的优先级，可以是函数指针、函数对象或Lambda表达式。

⭕需要注意的是，默认情况下，priority_queue使用std::less作为比较函数，即元素的优先级按照从大到小的顺序排列。如果需要按照从小到大的顺序排列，可以使用std::greater作为比较函数。

2. 特点

优先级排序：priority_queue中的元素按照一定的优先级进行排序。默认情况下，元素的优先级按照从大到小的顺序排列，也可以通过自定义的比较函数来指定不同的排序方式。
自动排序：在插入元素时，priority_queue会根据元素的优先级自动进行排序。每次插入新元素时，都会将新元素放置在正确的位置上。
取出优先级最高元素：priority_queue提供了一种方便的方式来取出优先级最高的元素。使用top()函数可以访问优先级最高的元素，而使用pop()函数可以将该元素从队列中移除。
底层实现采用堆：priority_queue通常使用堆（heap）数据结构来实现。堆是一种具有特定性质的二叉树，可以高效地插入新元素和取出优先级最高的元素。
动态大小：priority_queue的大小可以根据需要进行动态调整。可以随时插入新元素和删除已有元素，并在必要时自动重新排序。

⭕需要注意的是，priority_queue并不支持直接访问和修改除了优先级最高元素外的其他元素。如果需要对特定元素进行操作，通常需要先将其取出，然后再进行操作，最后再将其放回优先队列中。

二、priority_queue使用

1. 基本操作

包含头文件：首先，在使用priority_queue之前，你需要包含<queue>头文件。

#include <queue>

定义容器和比较函数：然后，你需要定义一个priority_queue对象，并指定元素类型和可选的比较函数（默认为std::less）。

std::priority_queue<int, std::vector<int>, std::less<int>> pq;

上面的示例定义了一个存储整数的优先队列，使用std::less作为比较函数，以便元素按照从大到小的顺序排列。

插入元素：你可以使用push()函数插入元素到priority_queue中。插入的元素会根据其优先级自动进行排序。

pq.push(3);
pq.push(1);
pq.push(4);
pq.push(1);

在上面的示例中，我们依次插入了4个整数到优先队列中。

访问和移除元素：你可以使用top()函数访问优先级最高的元素，使用pop()函数移除优先级最高的元素。

std::cout << pq.top() << std::endl;  // 访问优先级最高的元素
pq.pop();                           // 移除优先级最高的元素

在上面的示例中，我们先输出了优先级最高的元素，然后将其从队列中移除。

检查队列是否为空：你可以使用empty()函数来检查priority_queue是否为空。

if (pq.empty()) {
    // 队列为空
} else {
    // 队列不为空
}

下面的代码，演示了如何使用priority_queue：

#include <queue>
#include <iostream>

int main() {
    std::priority_queue<int, std::vector<int>, std::less<int>> pq;

    pq.push(3);
    pq.push(1);
    pq.push(4);
    pq.push(1);

    while (!pq.empty()) {
        std::cout << pq.top() << " ";
        pq.pop();
    }

    return 0;
}

输出结果为：4 3 1 1

在上面的代码中，我们创建了一个存储整数的优先队列pq，并依次插入了4个元素。然后，我们使用top()函数和pop()函数访问和移除元素，最后使用empty()函数检查队列是否为空。

2. 底层结构

priority_queue的底层通常使用堆（heap）数据结构来实现。堆是一种二叉树的数据结构（堆，数据结构详细介绍链接），具有以下特点：

堆结构是一个完全二叉树（Complete Binary Tree），即除了最后一层外，其他层都必须是满的，且最后一层的结点都靠左排列。
二叉堆分为最大堆（Max Heap）和最小堆（Min Heap）两种类型。
- 最大堆：每个父节点的值都大于或等于其子节点的值，即根节点的值最大。
- 最小堆：每个父节点的值都小于或等于其子节点的值，即根节点的值最小。

在priority_queue中，默认情况下采用最大堆实现，即优先级最高的元素存储在根节点，根节点的值最大。根据堆的性质，保证了在插入元素时，优先队列会根据元素的优先级进行自动排序，并在取出元素时能够取出优先级最高的元素。
在这里插入图片描述

三、priority_queue模拟实现

⭕ C++代码

#pragma once
#include<iostream>
using namespace std;
#include<vector>
namespace yws
{
	template<class T, class Container = vector<T>, class Compare = std::less<T>>
	class priority_queue
	{
	public:
		priority_queue()
		{}
		template <class Inputinterpreator>
		priority_queue(Inputinterpreator first, Inputinterpreator last)
		{
			while (first != last)
			{
				_con.push_back(*first);
				++first;
			}
			for (int i = (_con.size() - 1 - 1) / 2; i >= 0; --i)
			{
				adjust_down(i);
			}
		}
		void adjust_up(size_t child)
		{
			Compare com;
			size_t parent = (child - 1) / 2;
			while (child > 0)
			{
				if (com(_con[parent], _con[child]))
				{
					std::swap(_con[child], _con[parent]);
				}
				else
				{
					break;
				}
				child = parent;
				parent = (child - 1) / 2;
			}
		}
		void push(const T& x)
		{
			_con.push_back(x);
			adjust_up(_con.size() - 1);

		}
		void adjust_down(size_t parent)
		{
			Compare com;
			size_t child = (parent * 2) + 1;
			while (child < _con.size())
			{
				if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))
				{
					child = child + 1;
				}
				if (com(_con[parent], _con[child]))
				{
					std::swap(_con[parent], _con[child]);
				}
				else
				{
					break;
				}
				parent = child;
				child = (parent * 2) + 1;
			}
		}
		void pop()
		{
			std::swap(_con[0], _con[_con.size() - 1]);
			_con.pop_back();

			adjust_down(0);
		}
		const T& top()
		{
			return _con[0];
		}
		bool empty()  const
		{
			return _con.empty();
		}
		size_t size() const
		{
			return _con.size();
		}

	private:
		Container _con;
	};
}

⭕priority_queue中的仿函数

在priority_queue中，仿函数用于比较元素的优先级，并根据其返回值确定它们在队列中的位置。默认情况下，priority_queue使用std::less作为仿函数，也就是将元素按照从大到小的顺序进行排序。

你可以使用不同的仿函数来改变元素的排序方式。以下是一些常见的仿函数：

std::less<T>：对于基本数据类型和自定义类型，默认使用<运算符进行比较，按照从大到小的顺序排序。
std::greater<T>：对于基本数据类型和自定义类型，默认使用>运算符进行比较，按照从小到大的顺序排序。

除了上述默认提供的仿函数外，你还可以自定义仿函数来实现自定义的元素比较规则。自定义仿函数需要满足严格弱排序（Strict Weak Ordering）的要求，即：

比较关系必须是可传递的（transitive）：对于任意元素a、b和c，如果a与b比较相等，b与c比较相等，则a与c比较也相等。
比较关系不能是部分顺序（partial order）：对于任意元素a和b，它们不能同时大于、小于或等于彼此。
比较关系必须是可比较的（comparable）：比较关系的结果必须对所有元素定义明确的大小关系。

以下这段代码，演示了如何自定义一个仿函数来实现元素的自定义排序方式：

#include <iostream>
#include <queue>
#include <functional>

struct Person {
    std::string name;
    int age;

    Person(const std::string& n, int a) : name(n), age(a) {}
};

// 自定义仿函数
struct CompareByAge {
    bool operator()(const Person& p1, const Person& p2) const {
        return p1.age > p2.age;  // 按照年龄从小到大排序
    }
};

int main() {
    std::priority_queue<Person, std::vector<Person>, CompareByAge> pq;

    pq.push(Person("Alice", 25));
    pq.push(Person("Bob", 30));
    pq.push(Person("Charlie", 20));

    while (!pq.empty()) {
        Person p = pq.top();
        pq.pop();
        std::cout << p.name << " - " << p.age << std::endl;
    }

    return 0;
}

输出结果为：

Charlie - 20
Alice - 25
Bob - 30

在上面的代码中，我们定义了一个名为CompareByAge的结构体，重载了函数调用运算符operator()，按照Person对象的age成员进行比较。然后，我们将CompareByAge作为优先队列的仿函数类型，并插入3个Person对象到优先队列中。最后，我们按照自定义的排序方式依次取出元素并输出。

总结

优先队列是一种特殊的队列，其中存储的元素按照一定的优先级进行排列。在priority_queue中，优先级最高的元素能够快速被访问和删除。

首先，我们介绍了priority_queue的概念和特点。它是基于堆（heap）这种数据结构实现的，通常使用最大堆来进行内部排序。最大堆保证了根节点的值最大，并且任意节点的值大于或等于其子节点的值。这种特性使得优先队列能够高效地访问和删除具有最高优先级的元素。

接着，我们深入探讨了priority_queue的使用方法。基本操作包括插入元素、删除元素、访问元素和检查队列是否为空。

底层结构是priority_queue的关键部分，它通常使用堆来实现。在堆中，通过使用数组的索引来表示节点之间的关系，能够快速定位和操作元素。

最后，我们探讨了在priority_queue中使用的仿函数。仿函数用于确定元素之间的优先级，决定元素在队列中的位置。默认情况下，priority_queue使用std::less仿函数进行比较，对元素进行降序排列。你还可以选择其他仿函数或自定义仿函数来实现不同的排序方式。

温馨提示

感谢您对博主文章的关注与支持！在阅读本篇文章的同时，可以留下您宝贵的意见和反馈。如果您喜欢这篇文章，可以点赞、评论和分享给您的同学，这将对我提供巨大的鼓励和支持。另外，我计划在未来的更新中持续探讨与本文相关的内容。我会为您带来更多关于C++以及编程技术问题的深入解析、应用案例和趣味玩法等。请继续关注博主的更新，不要错过任何精彩内容！

再次感谢您的支持和关注。期待与您建立更紧密的互动，共同探索C++、算法和编程的奥秘。祝您生活愉快，排便顺畅！
在这里插入图片描述