代码随想录刷题60Day

---

目录

前言

整数拆分

N个数节点的二叉搜索树数量

---

前言

今天问题的难点在于从问题中抽象出dp数组和状态转移方程。

---

整数拆分

	int integerBreak1(int n) 
	{
		vector<int> dp(n + 1, 0);
		dp[1] = 1;
		for (int i = 2; i <= n; ++i)
			for (int j = 1; j < i; ++j)
				dp[i] = max(dp[i], j * max(i - j, dp[i - j]));
		return dp[n];
	}
	//为了减少一定的复杂度，可以进行一定的剪枝操作。
	int integerBreak(const int& n)
	{
		if (n < 4)return n - 1;
		vector<int> dp(n + 1, 0);
		dp[1] = 1;
		dp[2] = 2;
		dp[3] = 3;

		//这几个数都是原数比拆分后的数大
		for (int i = 4; i <= n; ++i)
		{
			for (int j = 2; j < i ; ++j)
				dp[i] = max(dp[i], max(j * dp[i - j], (i - j) * dp[j]));
		}
		return dp[n];
	}

N个数节点的二叉搜索树数量

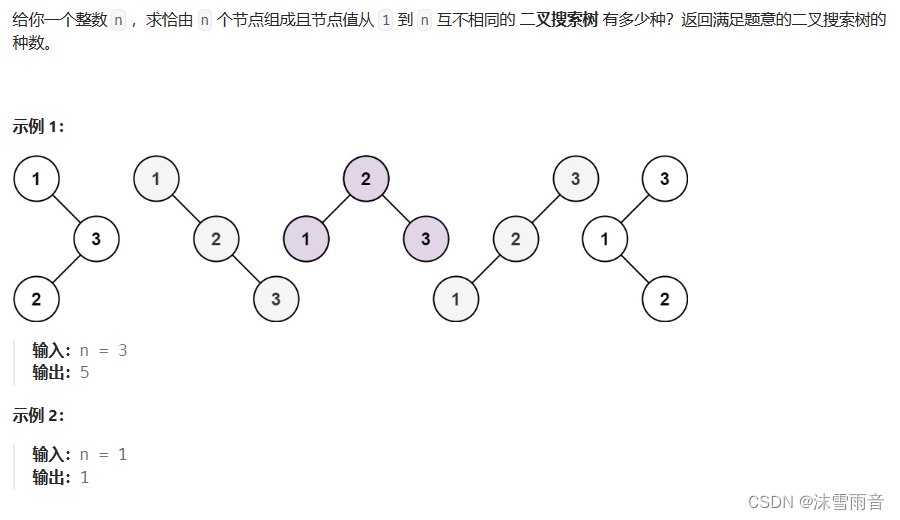
	int numTrees(int n) 
	{
		vector<int> dp(n + 1, 0);
		dp[0] = 1;
		dp[1] = 1;
		for (int i = 2; i <= n; ++i)
		{
			for (int j = 0; j <= (i - 1) / 2; ++j)
			{
				dp[i] += dp[j] * dp[(i - 1) - j] * 2;
				if (j == i - 1 - j)dp[i] -= dp[j] * dp[j];
			}
		}
		return dp[n];
	}