二叉树的顺序存储
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组,在逻辑上是一颗二叉树。

堆
概念
如果有一个关键码的集合K = {k0 ,k1 ,k2 ,k3…,k(n-1) },把它的所有元素按完全二叉树的顺序存储方式存储 在一个一维数组中,并满足Ki <= K(2*i+1)且Ki <= K(2*i+2)(Ki >= K(2*i+1)且Ki >= K(2*i+2)) i = 0,1, 2…,则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。


性质
堆中某个节点的值总是不大于或不小于其父节点的值。
堆总是一棵完全二叉树。
堆的实现
(本篇文章均采用小堆)
由于在物理上是一个数组,我们可以借助顺序表的思想
typedef int hpDataType;
typedef struct heap
{
hpDataType* a;
int size;
int capacity;
}HP;初始化与销毁
void HeapInit(HP* hp)
{
hp->a = NULL;
hp->size = 0;
hp->capacity = 0;
}
void HeapDestroy(HP* hp)
{
assert(hp);
hp->a = NULL;
hp->size = 0;
hp->capacity = 0;
}插入
由于堆的特性,头插改变堆的结构,所以我们选择尾插
void HeapPush(HP* hp, hpDataType x)
{
if (hp->size == hp->capacity)
{
int newCapacity = (hp->capacity + 1) * 2 - 1;
hpDataType* tmp = (hpDataType*)realloc(hp->a, sizeof(hpDataType)*newCapacity);
if (tmp == NULL)
{
printf("realloc error\n");
exit(-1);
}
hp->a = tmp;
hp->capacity = newCapacity;
}
hp->a[hp->size] = x;
hp->size++;
Adjustup(hp->a, hp->size - 1);
}
例如这样的一个堆,当我们在进行尾插时,这个数组的结构已经不符合堆的性质,所以我们要讲新插入的数据调整到合适的位置,我们称之为上调。
例如我们在上面的堆中插入一个20
我们通过比较它与它的父节点来判断是否进行交换
当它小于它的父节点或者它变为根节点时,变为小堆,停止交换

void Swap(hpDataType* m, hpDataType* n)
{
hpDataType mid = 0;
mid = *m;
*m = *n;
*n = mid;
}
void Adjustup(hpDataType* a, int child)
{
int parent = (child - 1) / 2;
while (child!=parent&&a[child] < a[parent])
{
Swap(&a[child], &a[(child - 1)/2]);
child = (child - 1) / 2;
parent = (child - 1) / 2;
}
}
void HeapPush(HP* hp, hpDataType x)
{
if (hp->size == hp->capacity)
{
int newCapacity = (hp->capacity + 1) * 2 - 1;
hpDataType* tmp = (hpDataType*)realloc(hp->a, sizeof(hpDataType)*newCapacity);
if (tmp == NULL)
{
printf("realloc error\n");
exit(-1);
}
hp->a = tmp;
hp->capacity = newCapacity;
}
hp->a[hp->size] = x;
hp->size++;
Adjustup(hp->a, hp->size - 1);
}删除
同样,删除分为头删和尾删,但在二叉树中,尾删并没有什么作用,而头删可以帮助我们选出最小(最大的数据),所以我们只考虑头删。
但若按照常规思路进行头删,会破坏堆的结构。

所以我们并不能采用常规的思路
这里我们可以将根节点与最后一个节点进行交换后进行尾删,然后将根节点(原本的最后一个节点)向下调整

可以看到,在我们进行向下调整的时候,我们比较的是父节点和左右孩子节点中较小的一个,这是因为若是比较较大的孩子节点,交换后被交换的孩子节点依然大于未被交换的孩子节点。无法构成小堆(大堆相反)
例如在第一次调整中,若是比较较大的孩子节点

交换后30依然会大于26
void Adjustdown(hpDataType* a, int size , int parent)
{
int leftChild = (parent + 1) * 2 - 1;
int rightChild = (parent + 1) * 2;
int min = 0;
while (leftChild<size)
{
if (rightChild < size && a[rightChild] < a[leftChild])
min = rightChild;
else
min = leftChild;
if (a[min] < a[parent])
{
Swap(&a[parent], &a[min]);
parent = min;
leftChild = (parent + 1) * 2 - 1;
rightChild = (parent + 1) * 2;
}
else
break;
}
}
void HeapPop(HP* hp)
{
assert(hp);
assert(hp->size);
Swap(&(hp->a)[0], &(hp->a)[hp->size - 1]);
hp->size--;
Adjustdown(hp->a,hp->size, 0);
}堆的相关问题
TopK问题
TopK问题,指的是在一个大小为n的数组中寻找最小(最大)的前K个的问题
在此之前,我们通常会运用排序来解决。
但若n较大,时间复杂度会很大。
同时,我们也可以构建大小为n的小堆(大堆)来解决。
但这同样存在问题,那就是若n较大,栈区无法存储。
因此我们可以构建一个大小为K的小堆(大堆),当存储前K个后,通过比较新数据与根节点数据,来判断是否进行插入,最后选择出最小(最大)的前K个数据。
void PrintTopK(int* a, int n, int k)
{
HP hp;
HeapInit(&hp);
for (int i = 0; i < k; i++)
{
HeapPush(&hp, a[i]);
}
for (int i = k; i < n; i++)
{
if (a[i] > HeapTop(&hp))
{
(hp.a)[0] = a[i];
Adjustdown(hp.a, k ,0);
}
}
for (int i = 0; i < k; i++)
{
printf("%d ", (hp.a)[i]);
}
printf("\n");
}堆排序
堆排序,指的是给出一个大小为n的数组,通过堆进行排序。
通常我们可以想到构建一个小堆(大堆),将数组一个个插入进去。
这样做空间复杂度为O(n)。
那么我们如何使空间复杂度达到O(1)呢?
首先我们默认为降序。
由于堆在物理上就是一个数组,所以我们可以直接对数组进行操作,使其首先构建成小堆(大堆)。我们可以先将第一个数据当做堆,在将后面的数据一个个插入(向上调整)

for (int i = 1; i < n; i++)
{
Adjustup(a, i);
}另外,我们还有另外一种方法
我们可以向下调整。但向下调整的前提是左右子树都为小堆(大堆)。因此,我们需要从最后一个非叶子节点(叶子节点没有左右子树,不需要调整)开始向下调整。

在构建好小堆(大堆)后,我们便可以进行排序的操作。
由于是对原数组进行操作,我们无法做到将根节点赋值给数组后进行删除。但在头删中,我们是将根节点与最后一个节点交换后向下调整,由于小堆的根节点最小,那么最小的数便被放置在数组的末尾,并且将其排除在堆外。

那么在第二次删除后,数组中倒数第二个数据便为15(第二小)。
由此可知,我们只需要不断进行删除操作,便能将小堆转变为降序
(注意:降序需要小堆,升序需要大堆,一定不要搞反)
如此,我们便可以完成堆排序
void HeapSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
Adjustup(a, i);
}
for (int i = n-1; i > 0 ; i--)
{
Swap(&a[i], &a[0]);
Adjustdown(a, i, 0);
}
}构建堆的时间复杂度
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化使用满二叉树来证明(时间复杂度本来看的 就是近似值,多几个节点不影响最终结果)。
在堆排序中,我们讲述了构建堆的方法,我们可以统计各层节点的数量和移动层数来进行计算。

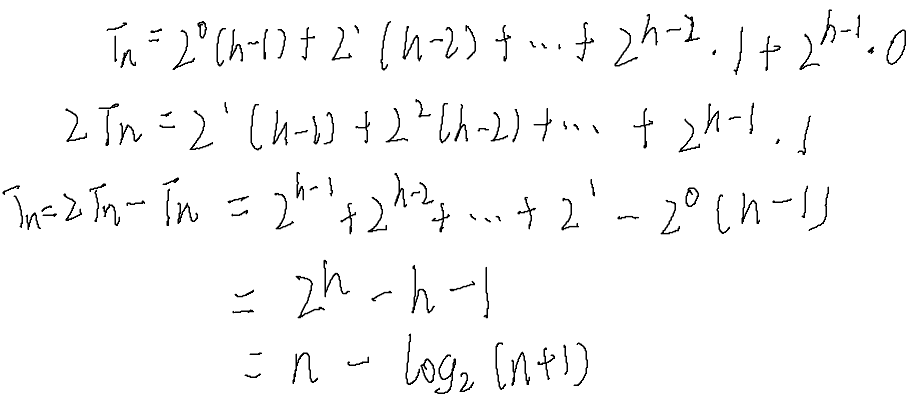
因此可以得出:构建堆的时间复杂度为O(N)









![[附源码]Nodejs计算机毕业设计基于的仓库管理系统Express(程序+LW)](https://img-blog.csdnimg.cn/feeef451e0254f3d80283edf7f586dbc.png)