💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

2.1 基于线性离散最优潮流（OPF）模型的配电网规划( DNP )

 2.2 基于线性潮流最优潮流( OPF )的配电网规划( DNP )

🌈3 Matlab代码实现

🎉4 参考文献

---

💥1 概述

最有潮流 （OPF） 问题确定一个网络工作点，该工作点可最小化特定目标，例如发电成本或功率损耗。它是非凸的。我们证明了径向电力网络在略微收缩OPF可行集后，在温和条件下求解二阶锥程序可以获得OPF的全局最优值。可以先验检查该条件，并适用于IEEE 13、34、37、123总线网络和两个实际网络。

配电系统中的电容器分配问题涉及通过电容器安装最大限度地降低能量和峰值功率损耗.

发电站产生的电力通过大型复杂的输配电网络设备，如变压器、架空线、电缆等，到达最终用户。由于电力系统中的感性负载，发电站产生的电能单位与分配给消费者的单位不匹配。网络中丢失了一定百分比的单元。这种损失的最大部分是“配电网损失”。电容放置是降低损耗的最实用方法。它还改善了功率因数和电压曲线。优化电容器安装的重要一点是找到必须放置在网络上的电容器的尺寸、位置和数量。本文提出了一种在径向网络中优化电容器组放置的方法，目的是最小化损耗和增强电压。

📚2 运行结果

2.1 基于线性离散最优潮流（OPF）模型的配电网规划( DNP )

 

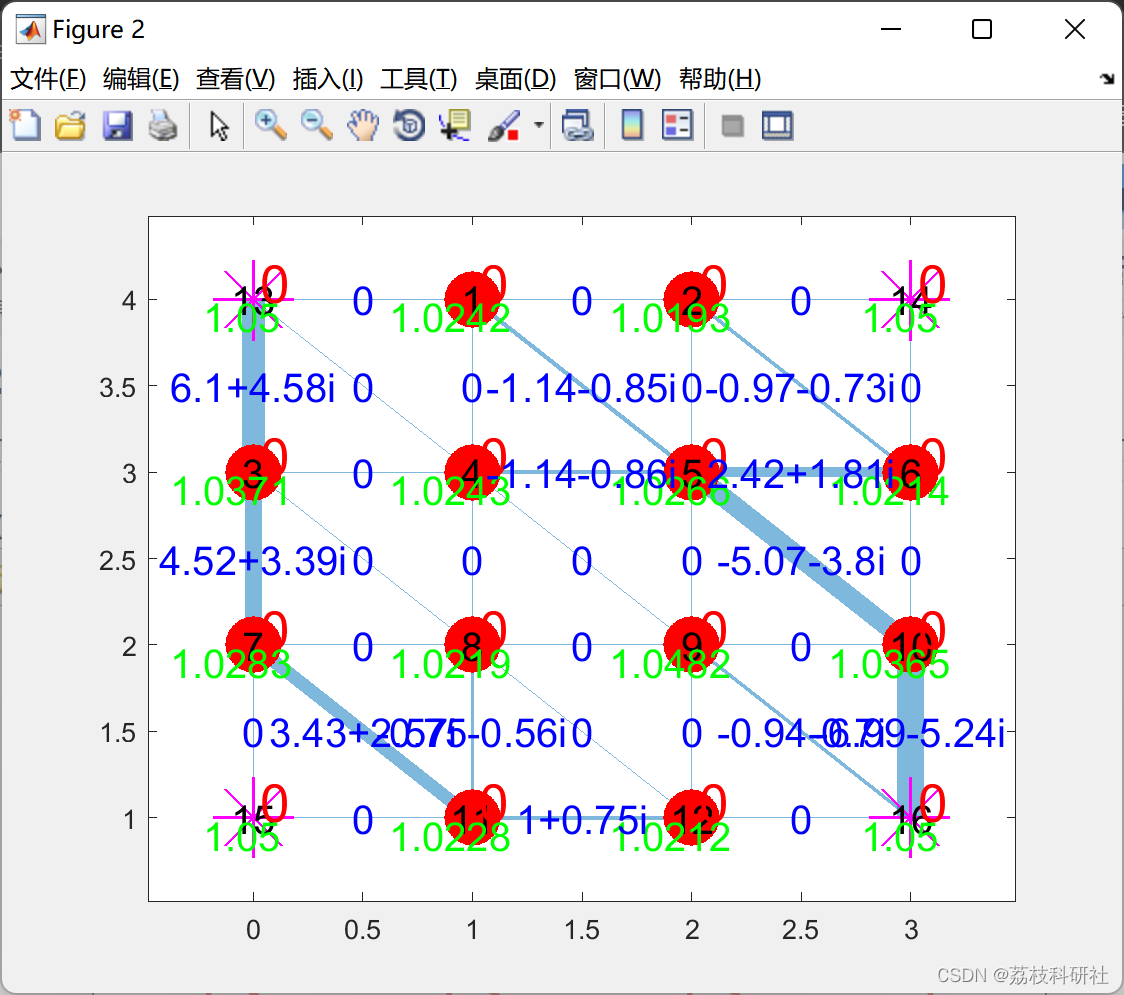
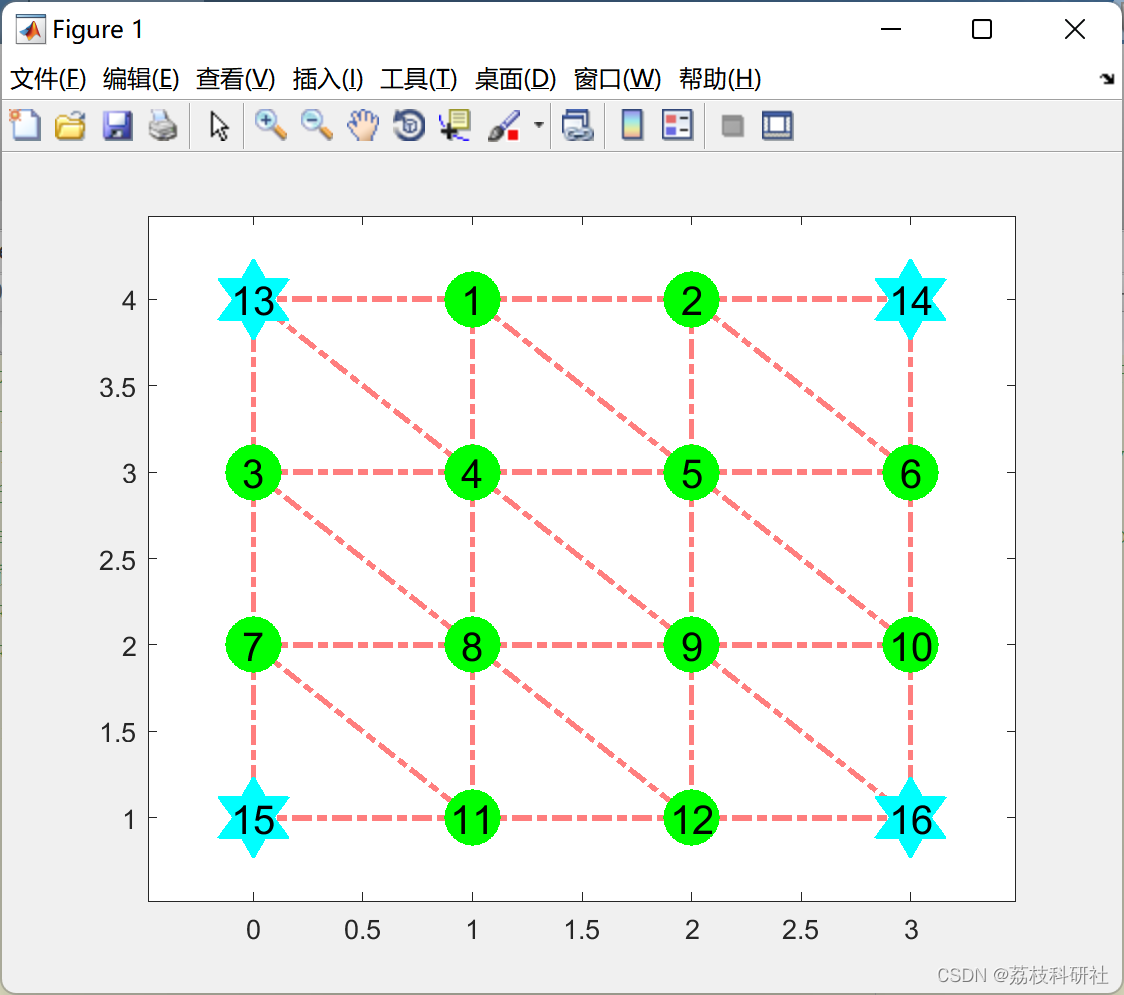
 2.2 基于线性潮流最优潮流( OPF )的配电网规划( DNP )

 

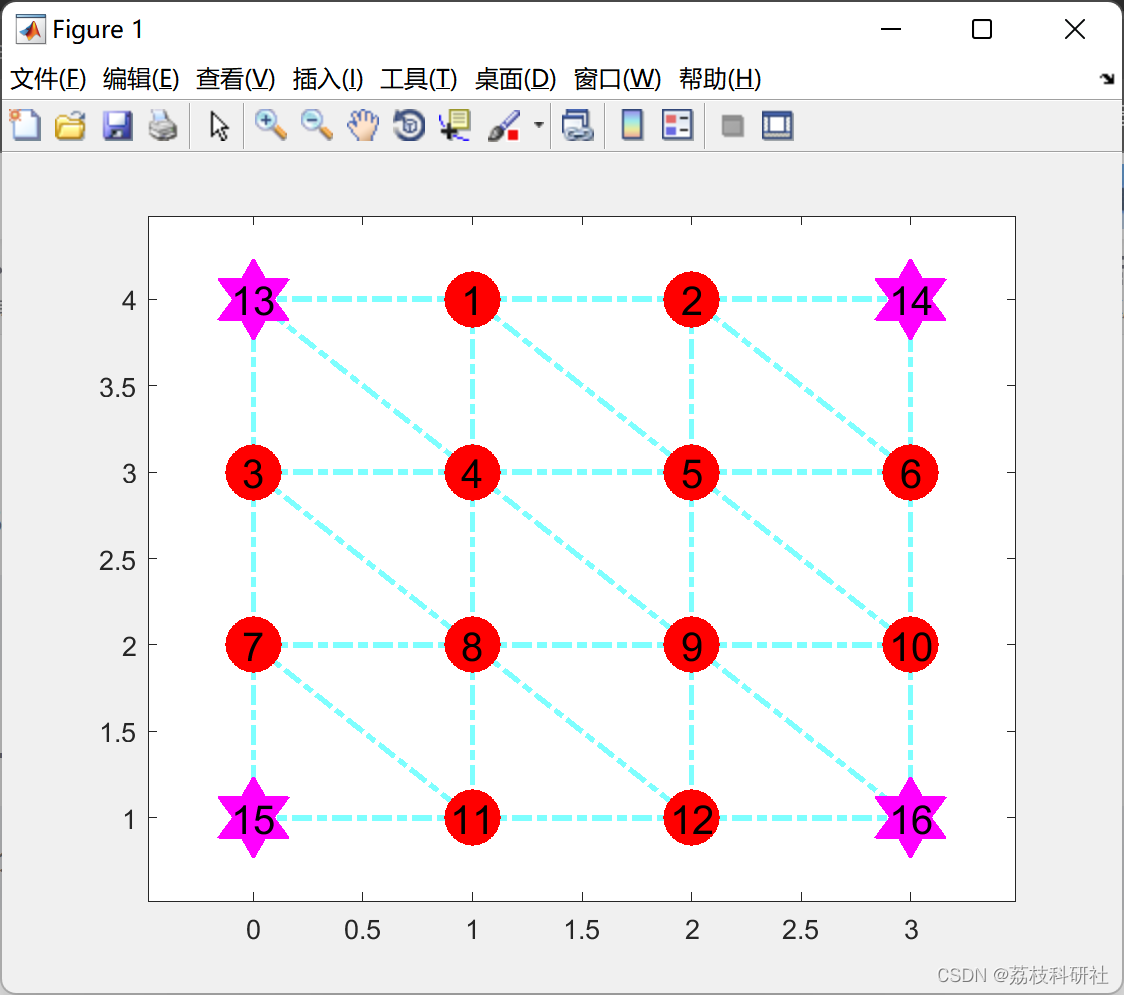
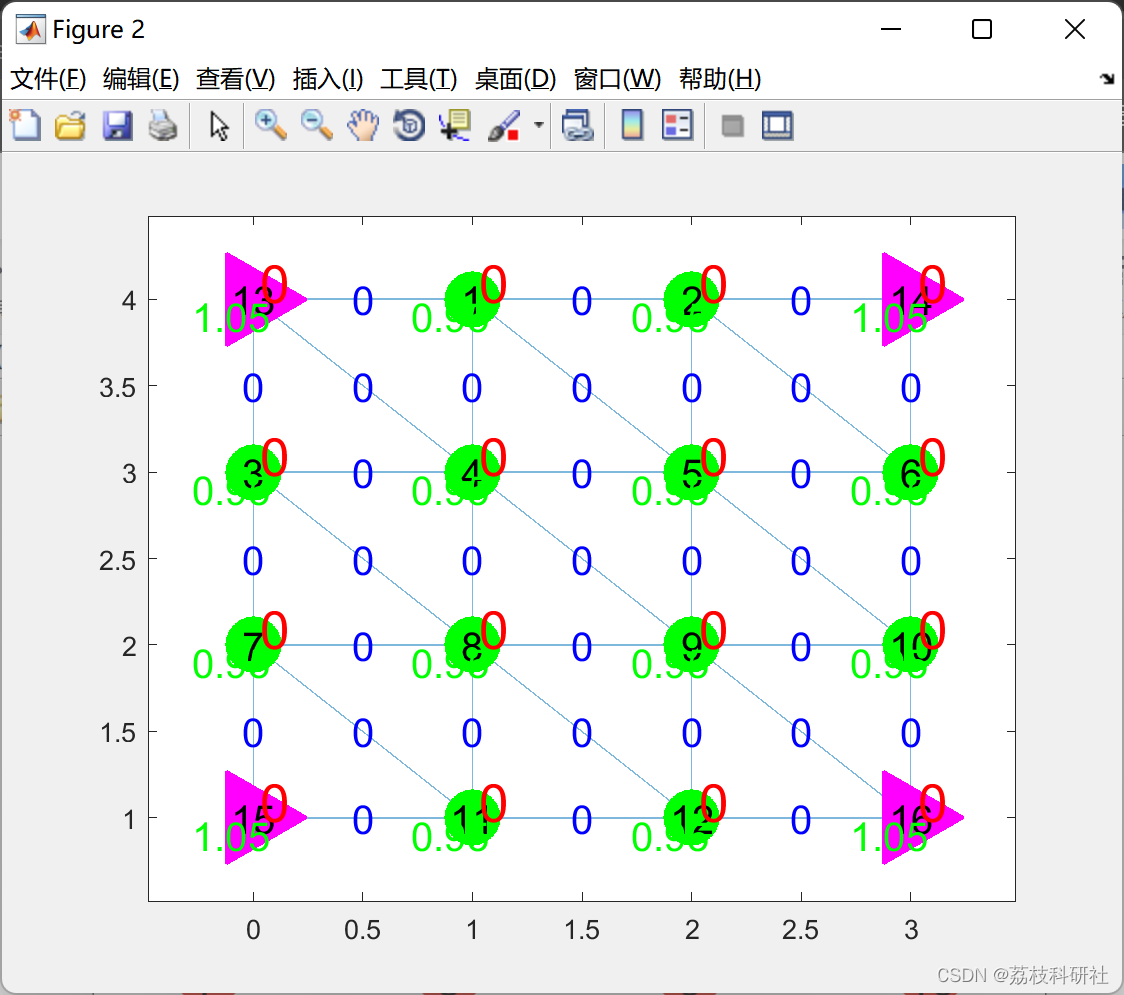
🌈3 Matlab代码实现

回复关键字

🎉4 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]M. E. Baran and F. F. Wu, “Optimal capacitor placement on radial distribution systems,” IEEE Trans. Power Delivery, vol. 4, no. 1, pp. 725–734,1989.
[2]M. E. Baran and F. F. Wu, “Optimal sizing of capacitors placed on a radial distribution system,” IEEE Trans. Power Delivery, vol. 4, no. 1, pp. 735–743, 1989
[3]L. Gan, N. Li, U. Topcu and S. H. Low, "Exact Convex Relaxation of Optimal Power Flow in Radial Networks," in IEEE Transactions on Automatic Control, vol. 60, no. 1, pp. 72-87, Jan. 2015, doi: 10.1109/TAC.2014.2332712.