🔥博客主页:小王又困了
📚系列专栏:每日一练
🌟人之为学,不日近则日退
❤️感谢大家点赞👍收藏⭐评论✍️
目录
一、选择题
📝1.第一题
📝2.第二题
📝3.第三题
二、编程题
📝1.第一题
📝2.第二题
🗒️前言:
在前面我们学习完C语言的所以知识,当然练习巩固也不能落下。俗话说:“无财之谓贫,学而不能行之谓病。”可见实践对我们学习的重要。接下来就让小王带着大家进行练习,巩固我们C语言的学习。
一、选择题
📝1.第一题
下列程序的输出结果是什么( )
int main()
{
int n = 1001;
int ans = 0;
for(int i = 1; i <= n; ++i)
{
ans ^= i % 3;
}
printf("%d",ans);
return 0;
}💡解题思路:
这道题考查了我们对异或操作符的理解,异或的计算规则是:两个数对应的二进制位相同为0,相异为1。还有特殊的规律:两个相同的数异或为0;任何数与0异或还是这个数。
使用for循环遍历从1到n的所有整数。在每次迭代中,都会计算当前整数 i 对3取余的结果,然后将这个结果与 ans 进行异或操作。对 i 取余的结果有1,2,0循环1001次,这三个数出现333次,多出1,2。偶数对异或的结果就是0,最后剩下 1^2^0^1^2 ,最后的结果为0。
📝2.第二题
下面代码的结果是()
#include <stdio.h>
int i;
int main()
{
i--;
if (i > sizeof(i))
{
printf(">\n");
}
else
{
printf("<\n");
}
return 0;
}💡解题思路:
在C语言中,0为假,非0为真。全局变量没有给初始值时,编译器会默认将其初始化为0。
i 的初始值为0,i-- 的结果为-1,i 为整型,sizeof(i)求 i 类型的大小为4,按这样的分析来看,结果应该打印 ‘<’ ,但是sizeof的返回值的类型为无符号整型,因此编译器会自动将左侧的 i 自动转化为无符号整型的数据,-1的二进制序列的补码全为1,对应的无符号整型是非常大的数,超过4或8,所以结果应该打印 ‘>’。
📝3.第三题
下面代码的结果是()
int main()
{
int a, b, c;
a = 5;
c = ++a;
b = ++c, c++, ++a, a++;
b += a++ + c;
printf("a=%d b=%d c=%d\n", a, b, c);
return 0;
}💡解题思路:
我们想要解决这道题要了解几个知识点:
- ++i 与 i++ 的区别:一个是先加在使用,一个是先使用在加
- 逗号运算符的作用:含有逗号运算符的表达式,它的值为最后一个表达式的值
- 运算符的优先级:1.++,+的优先级比+=高 2.逗号运算符的优先级比赋值运算符的优先级低 3.多个+号在一起,其优先级为后置++,+,前置++,例如:a+++c, 可拆分为(a++)+c
了解这些我们就可以开始做题啦。我们一步一步执行代码:
二、编程题
📝1.第一题

💡解题思路:
我们直接遍历范围内的整数,分别判断每个整数是否是自除数。在判断自除数时,要得到整数的每一位,每次对整数 %10 就可以得到整数的最后一位,然后除以10。重复该操作,依次得到整数每一位,当整数变成0就遍历完一个整数。如果每一位都可以将整数整除,那么这个数就是自除数。这里要注意:得到的最后一位是0时,由于0不能做除数,一定不是自除数。
bool isSelfDividing(int num) { int temp = num; while (temp > 0) { int digit = temp % 10; if (digit == 0 || num % digit != 0) { return false; } temp /= 10; } return true; } int* selfDividingNumbers(int left, int right, int* returnSize) { int* arr = (int*)malloc(sizeof(int) * (right - left + 1)); int pos = 0; for (int i = left; i <= right; i++) { if (isSelfDividing(i)) { arr[pos++] = i; } } *returnSize = pos; return arr; }
📝2.第二题

💡解题思路:
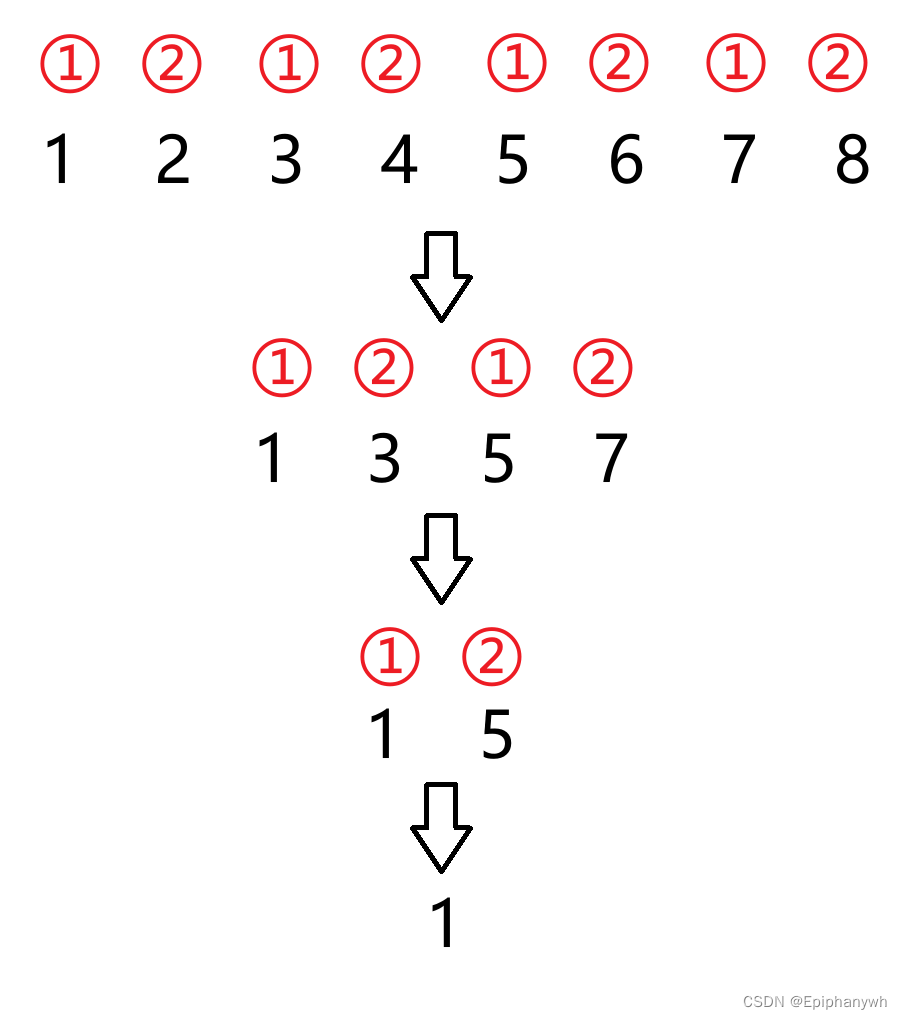
我们可以使用异或的思想,将数组中的数和 1-n 的数依次异或一遍,得到的就是重复的数和丢失的数异或的结果。因为其他数都成对出现,异或的结果就为0。我们只要在通过排序,遍历数组找到重复的数,再将重复的数与刚刚的数异或,就可以得到丢失的数。
int cmp_int(const void* p1, const void* p2) { return (*(int*)p1 - *(int*)p2); } int* findErrorNums(int* nums, int numsSize, int* returnSize) { int* newarr = (int*)malloc(sizeof(int*) * 2); int i = 0; int num = 0; for (i = 0; i < numsSize; i++) { num ^= nums[i]; } for (i = 1; i <= numsSize; i++) { num ^= i; //会得到重复的数和丢失的数异或的结果 } //排序 qsort(nums, numsSize, sizeof(int), cmp_int); for (i = 0; i < numsSize - 1; i++) { //找重复的数 if (nums[i] == nums[i + 1]) { break; } } //得到丢失的数 num ^= nums[i]; newarr[0] = nums[i]; newarr[1] = num; *returnSize = 2; return newarr; }
本次的内容到这里就结束啦。希望大家阅读完可以有所收获,同时也感谢各位读者三连支持。文章有问题可以在评论区留言,博主一定认真认真修改,以后写出更好的文章。你们的支持就是博主最大的动力。