面试题中的考查:

其实这个就是一个约瑟夫问题,下面通过讲解你会很好的解决这道题目。
故事背景:
据说在罗马帝国时期,一群犹太士兵被罗马人包围,为了不当罗马人的俘虏,犹太士兵们决定集体自杀,自杀的方式是所有人围成一个圈,第一个士兵会杀掉他左面的第二个士兵,同样,第三个士兵杀掉第四个士兵……以此类推,知道最后只剩下一个人,然后他再自杀。犹太士兵里有个人叫约瑟夫,他想投降保命但又不敢明说,那么约瑟夫应该站在那个位置才能够活下来?
其实这个问题,可以简化出两个模型:
(一)去1留2
去1留2是指:n个人进行1、2循环报数,报1的人离开,报2的人留下,那么最后留下的人是原来的几号?
-
当总人数是2的n次方形式
例如当人数为4(2的2次方)时,进行循环报数,最后留下来的人是原来的几号?
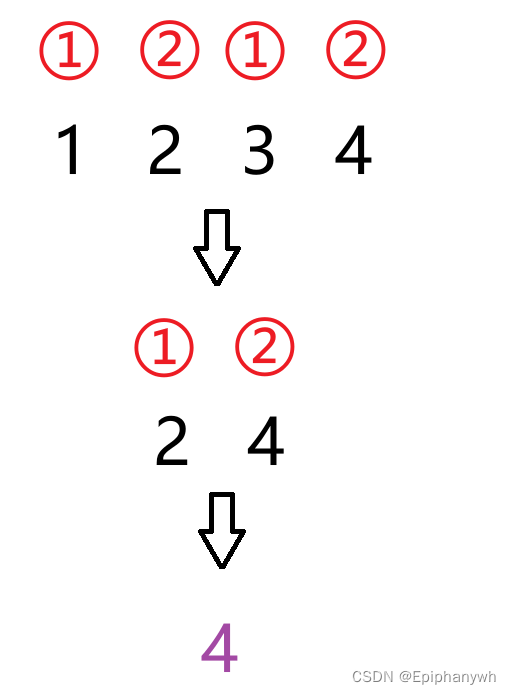
由图中可以看到,最后留下来的数字是4.
当人数为8(2的3次方)时,进行循环报数,最后留下来的人是原来的几号?
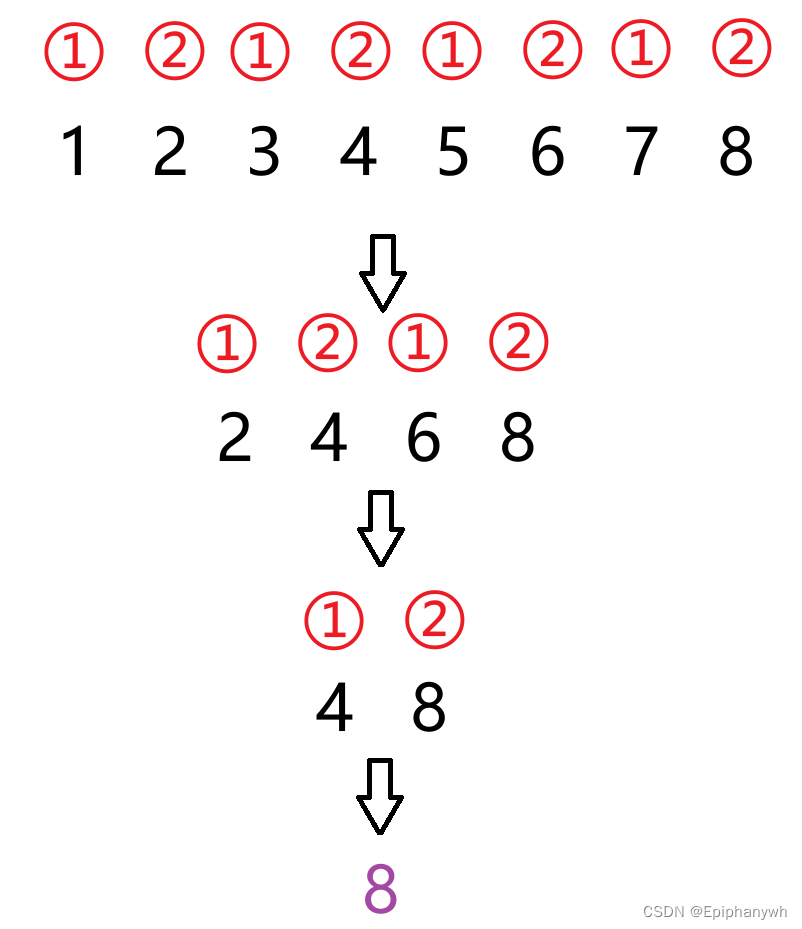
最后留下来的数字是8.
再多举几个例子,我们可以发现规律:当总人数是2的n次方形式时,最后留下来的数字是第2的n次方个,即最后一个。
-
当总人数不是2的n次方形式
这里可以利用转化思想:将人数不是2的n次方形式转化成是2的n次方形式,在利用上面的规律,便可以得到最后留下来的数字。
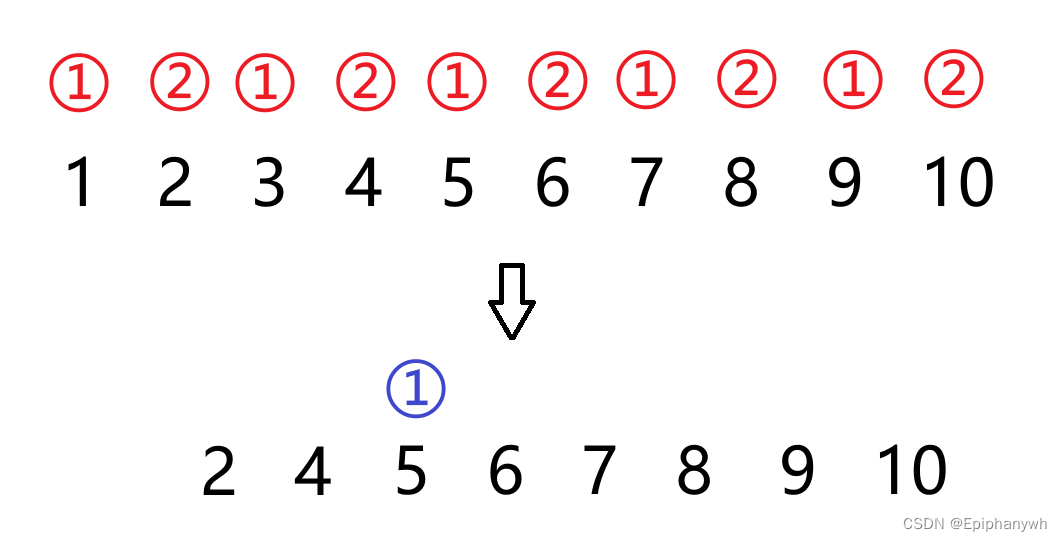
例如,当人数是6时,我们可以将6写成4+2,即 6-2=4: 如果我们先去掉两个数字1、3,剩余的数字个数(2、4、5、6)就是2的n次方个,这时留下的数字就是剩余人数的最后一个。
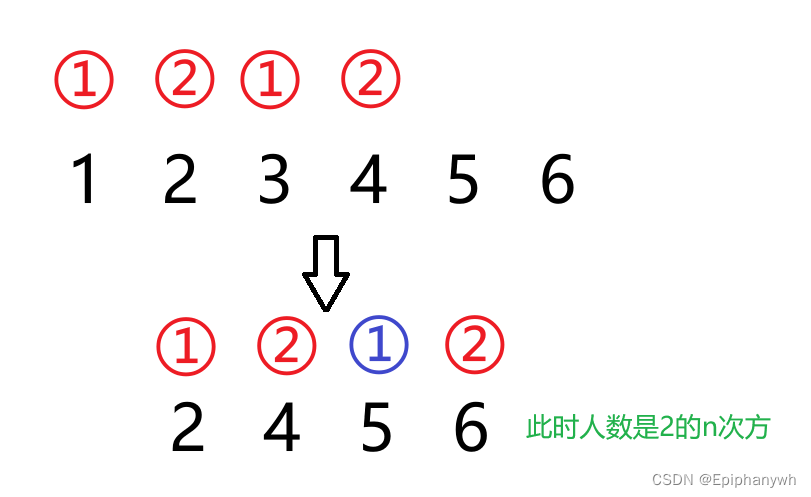
但是要注意,此时剩余的数字的开头不是2,而是5,相当于5成为新的开头,是进行第一个报数的,相对的4就是最后一个,所以最后一个数字就是4.
我们也可以发现,最后一个数字就是第一个报数5的前一个,而这个数就是起初要淘汰俩个人进行报数的最后一个(1、2、3、4),所以可以总结出一个公式:
当人数为x时,x = a+2的n次方(a大于等于0);
留下来的数字是原来的y号,y = 2*a。
我们可以来验证一下:例如当人数为10个人时,x = 2+2的3次方;y = 2*2 = 4,所以最后一个数字是原来的四号。
(二)去2留1
去1留2是指:n个人进行1、2循环报数,报2的人离开,报1的人留下,那么最后留下的人是原来的几号?
-
当总人数是2的n次方形式
例如当人数为4(2的2次方)时,进行循环报数,最后留下来的人是原来的几号?
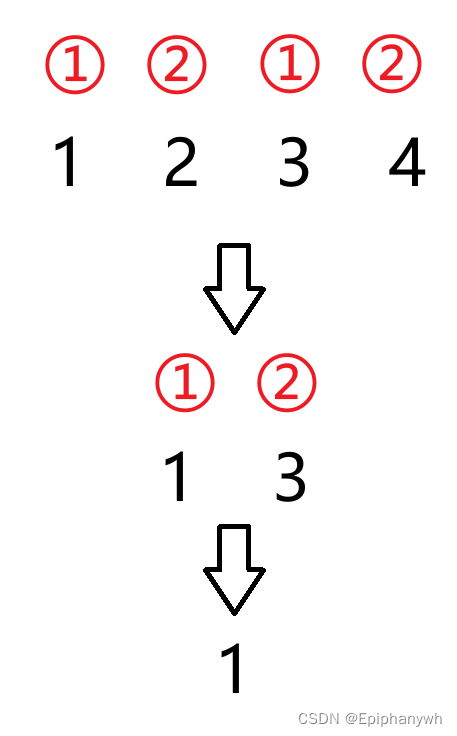
当人数为8(2的3次方)时,进行循环报数,最后留下来的人是原来的几号?
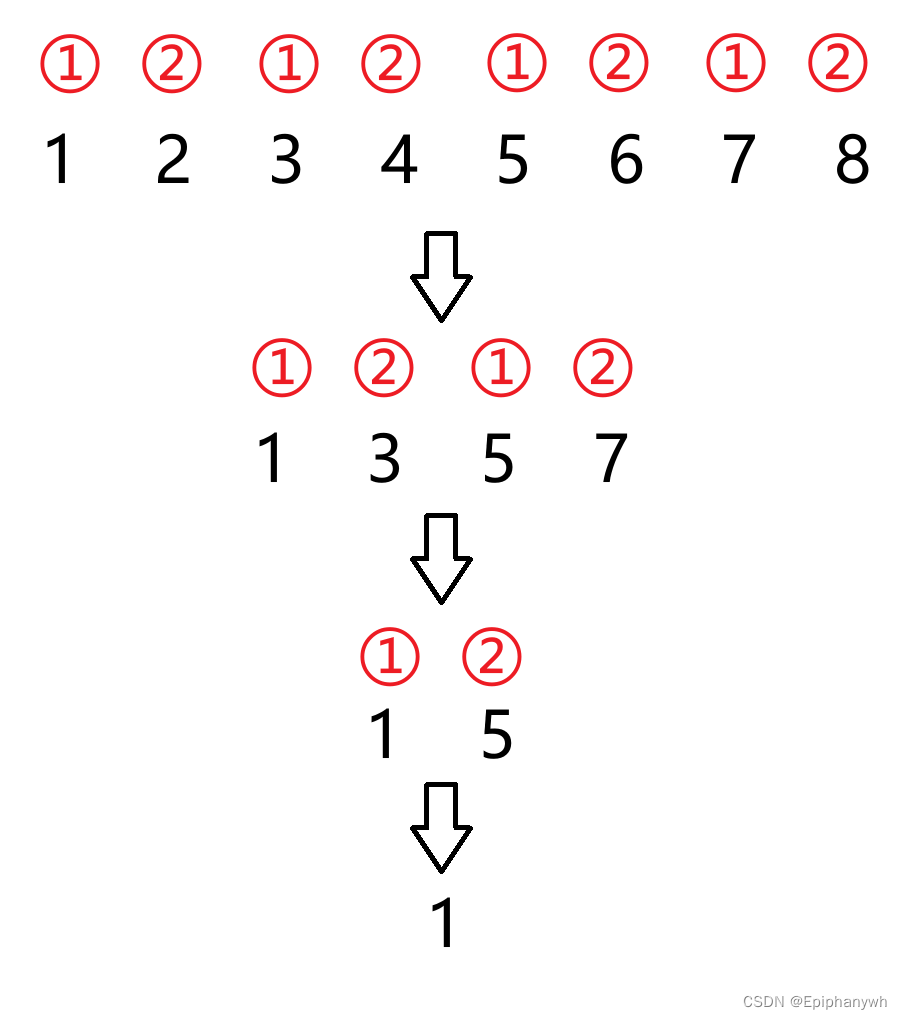
由两个例子可以看出,留下来的数字是原来第一个报数的。
再多举几个例子,我们可以发现规律:当总人数是2的n次方形式时,最后留下来的数字是第一个报数的人。
-
当总人数不是2的n次方形式
这里可以利用转化思想:将人数不是2的n次方形式转化成是2的n次方形式,在利用上面的规律,便可以得到最后留下来的数字。
利用同样的分析方法,我们可以得到结论:
当人数为x时,x = a+2的n次方(a大于等于0);
留下来的数字是原来的y号,y = 2*a+1。
再回到我们的面试题,"单数"指的是奇数,教练下令“单数运动员出列”即为要求奇数编号的运动员出列。奇数也就代表1、3、5……之类的数,也就是上述讲解的 “去1留2”模型,带入公式,我们可以得到最后一个运动员是最开始的第几号:
50 = 32 + 18;则留下来的运动员是最开始的2*18号,也就是36号。
本次内容到此结束了!如果你觉得这篇博客对你有帮助的话 ,希望你能够给我点个赞,鼓励一下我。感谢感谢……
参考资料:
【小学数学—约瑟夫站位问题】https://www.bilibili.com/video/BV1hh411J7Hx?vd_source=564abed1c36a31978eb9de7cdc6668d2
封面获取:
【你应该站在哪个位置,才能活到最后?】https://www.bilibili.com/video/BV1KM4y1V7tQ?vd_source=564abed1c36a31978eb9de7cdc6668d2