接雨水——单调栈

题目链接

---

单调递增的栈还是单调递减的栈

我们常说的**”积水成洼“**，指的就是说：当两边地势高于中间的地势时，中间的区域就成了洼地，也就可以积水了。

这一题就是如此，我们需要通过一个栈来记录数据，只要记录的数据有高——低——高这一过程，就说明形成了洼地，也就可以计算雨水容量了。

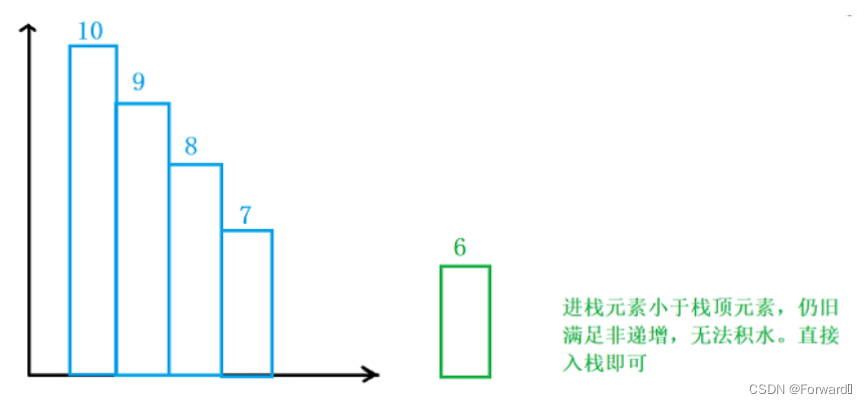
所以我们应该用一个非递增的栈来存放数据，我们保证栈中的数据是非递增的，这样当一个数据准备进栈时，如果进栈元素小于栈顶元素，那就仍旧满足非递增顺序，直接入栈即可，而如果进展元素大于栈顶元素，就说明栈顶元素的前一个元素，栈顶元素，进栈元素这三个元素达成了高——低——高这一条件，也就可以进行容量的计算了。

---

实现思路

我们已经知道要用非递增的单调栈来解决这个问题，那么接下来就要讨论如何做具体的实现了。

这里我们利用栈来储存数组元素的下标。

规定栈顶元素为stack_top，栈顶元素的前一个为left（注意：二者都是构成容器的数组元素的下标）

我们用i来遍历构成容器的数组，需要分以下几种情况讨论：

• 当栈为空或者进栈元素小于栈顶元素时，进栈元素height[i]直接入栈即可。如图：

• 否则，当栈不为空并且进栈元素大于栈顶元素时，为保证栈的非递增特性，要通过循环不断移除栈元素，同时：

  • 如果出栈顶元素后栈为空，那么直接将进栈元素height[i]入栈即可。如图：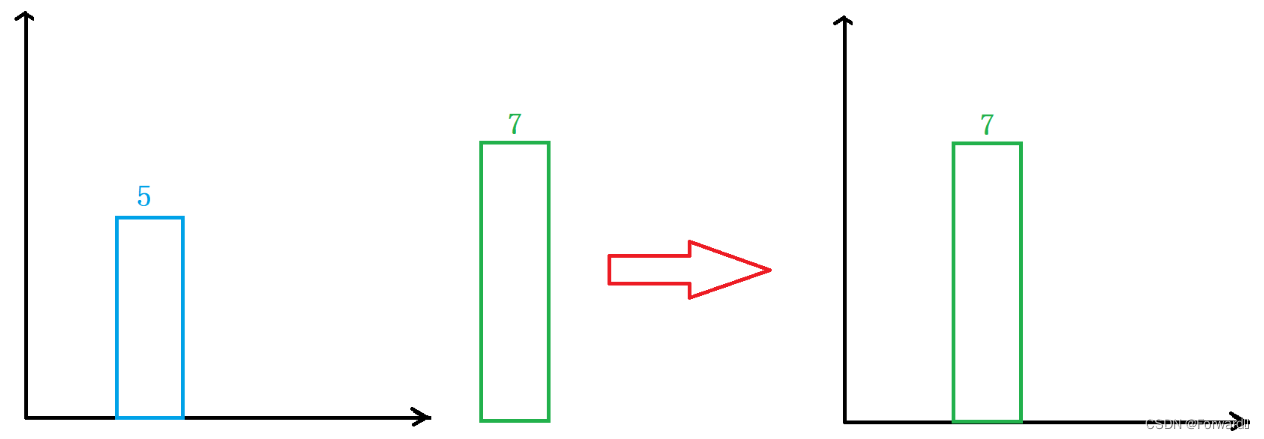

    

  • 如果出栈顶元素后栈不为空，那么栈顶元素的前一个元素height[left]、栈顶元素height[stack_top]、进栈元素height[i]就达成了高——低——高的条件，即形成了积水区域。积水区域的宽wide就是i - left - 1，高度high就是min(height[i], height[left] - height[stack_top])，最后容积也就是wide * high。如图：

    

接下来，我们以题目中的例子height = [0,1,0,2,1,0,1,3,2,1,2,1]为例，模拟整个过程。

实现代码

int trap(int* height, int heightSize){
    //申请栈空间
    int *stack = (int*)malloc(sizeof(int) * heightSize);
    int top = 0;

    int volum = 0;  //容量

    for (int i=0; i<heightSize; i++)
    {
        //如果栈不为空并且遍历元素大于栈顶元素
        //由于要保证栈的单调性，所以无论如何栈顶元素都要出栈
        while (top != 0 && height[i] > height[stack[top - 1]])
        {
            int stack_top = stack[--top];

            //如果栈顶元素出栈后仍不为空，就说明可以容纳雨水
            if (top != 0)
            {

                //计算容量
                int left = stack[top - 1];
                int wide = i - left - 1;
                int high = fmin(height[left], height[i]);

                volum += wide * (high - height[stack_top]);
            }

            //如果计算完这一次后仍满足循环条件，就说明还可能继续装水
        }
        //无论是否进入循环，遍历元素都要入栈
        stack[top++] = i;
    }

    //释放栈空间
    free(stack);
    return volum;
}