文章目录
- 前言
- 一、示例代码
- 二、示例代码解读
- 1.线性回归模型
- 2.MSE损失函数
- 3.优化过程
- 4.结果解读
- 总结
前言
在机器学习和数据科学中,线性回归是一种常见而重要的方法。本文将以一个简单的代码示例为基础,介绍线性回归的基本原理和应用。将使用Python和NumPy库来实现一个简单的线性回归模型和使用最小均方误差(MSE)损失函数来衡量模型的拟合准确性,并通过优化权重参数来提高模型的性能。
一、示例代码
import numpy as np
import matplotlib.pyplot as plt
# 准备数据
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = 0.0 # 定义并初始化权重参数
# 定义模型
def forward(x):
return x*w
# 定义损失函数
def loss(x, y):
y_pred = forward(x)
return (y_pred-y) * (y_pred-y)
# 存放权重和损失值,保留在列表里面
w_list = []
mse_list = []
# 生成0.0-4.0,步长值为0.1的序列
for w in np.arange(0.0, 4.1, 0.1):
print('w=',w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data): # 将x_data和y_data进行组合成一个新的迭代器,相当于【(x_data【0】,y_data【0】),(x_data【1】,y_data【1】)】
y_pred_val = forward(x_val) # 计算预测值
loss_val = loss(x_val, y_val) # 计算损失
l_sum += loss_val # 将这一轮中的损失值进行累加,用于计算平均损失值
print('\t', x_val, y_val, y_pred_val, loss_val)
print('MSE=', l_sum / 3)
w_list.append(w)
mse_list.append(l_sum / 3)
# 在绘图中显示
plt.plot(w_list, mse_list)
plt.ylabel('loss')
plt.xlabel('w')
plt.show()
代码结果:
w= 0.0
1.0 2.0 0.0 4.0
2.0 4.0 0.0 16.0
3.0 6.0 0.0 36.0
MSE= 18.666666666666668
w= 0.1
1.0 2.0 0.1 3.61
2.0 4.0 0.2 14.44
3.0 6.0 0.30000000000000004 32.49
MSE= 16.846666666666668
w= 0.2
1.0 2.0 0.2 3.24
2.0 4.0 0.4 12.96
3.0 6.0 0.6000000000000001 29.160000000000004
MSE= 15.120000000000003
w= 0.30000000000000004
1.0 2.0 0.30000000000000004 2.8899999999999997
2.0 4.0 0.6000000000000001 11.559999999999999
3.0 6.0 0.9000000000000001 26.009999999999998
MSE= 13.486666666666665
w= 0.4
1.0 2.0 0.4 2.5600000000000005
2.0 4.0 0.8 10.240000000000002
3.0 6.0 1.2000000000000002 23.04
MSE= 11.946666666666667
w= 0.5
1.0 2.0 0.5 2.25
2.0 4.0 1.0 9.0
3.0 6.0 1.5 20.25
MSE= 10.5
w= 0.6000000000000001
1.0 2.0 0.6000000000000001 1.9599999999999997
2.0 4.0 1.2000000000000002 7.839999999999999
3.0 6.0 1.8000000000000003 17.639999999999993
MSE= 9.146666666666663
w= 0.7000000000000001
1.0 2.0 0.7000000000000001 1.6899999999999995
2.0 4.0 1.4000000000000001 6.759999999999998
3.0 6.0 2.1 15.209999999999999
MSE= 7.886666666666666
w= 0.8
1.0 2.0 0.8 1.44
2.0 4.0 1.6 5.76
3.0 6.0 2.4000000000000004 12.959999999999997
MSE= 6.719999999999999
w= 0.9
1.0 2.0 0.9 1.2100000000000002
2.0 4.0 1.8 4.840000000000001
3.0 6.0 2.7 10.889999999999999
MSE= 5.646666666666666
w= 1.0
1.0 2.0 1.0 1.0
2.0 4.0 2.0 4.0
3.0 6.0 3.0 9.0
MSE= 4.666666666666667
w= 1.1
1.0 2.0 1.1 0.8099999999999998
2.0 4.0 2.2 3.2399999999999993
3.0 6.0 3.3000000000000003 7.289999999999998
MSE= 3.779999999999999
w= 1.2000000000000002
1.0 2.0 1.2000000000000002 0.6399999999999997
2.0 4.0 2.4000000000000004 2.5599999999999987
3.0 6.0 3.6000000000000005 5.759999999999997
MSE= 2.986666666666665
w= 1.3
1.0 2.0 1.3 0.48999999999999994
2.0 4.0 2.6 1.9599999999999997
3.0 6.0 3.9000000000000004 4.409999999999998
MSE= 2.2866666666666657
w= 1.4000000000000001
1.0 2.0 1.4000000000000001 0.3599999999999998
2.0 4.0 2.8000000000000003 1.4399999999999993
3.0 6.0 4.2 3.2399999999999993
MSE= 1.6799999999999995
w= 1.5
1.0 2.0 1.5 0.25
2.0 4.0 3.0 1.0
3.0 6.0 4.5 2.25
MSE= 1.1666666666666667
w= 1.6
1.0 2.0 1.6 0.15999999999999992
2.0 4.0 3.2 0.6399999999999997
3.0 6.0 4.800000000000001 1.4399999999999984
MSE= 0.746666666666666
w= 1.7000000000000002
1.0 2.0 1.7000000000000002 0.0899999999999999
2.0 4.0 3.4000000000000004 0.3599999999999996
3.0 6.0 5.1000000000000005 0.809999999999999
MSE= 0.4199999999999995
w= 1.8
1.0 2.0 1.8 0.03999999999999998
2.0 4.0 3.6 0.15999999999999992
3.0 6.0 5.4 0.3599999999999996
MSE= 0.1866666666666665
w= 1.9000000000000001
1.0 2.0 1.9000000000000001 0.009999999999999974
2.0 4.0 3.8000000000000003 0.0399999999999999
3.0 6.0 5.7 0.0899999999999999
MSE= 0.046666666666666586
w= 2.0
1.0 2.0 2.0 0.0
2.0 4.0 4.0 0.0
3.0 6.0 6.0 0.0
MSE= 0.0
w= 2.1
1.0 2.0 2.1 0.010000000000000018
2.0 4.0 4.2 0.04000000000000007
3.0 6.0 6.300000000000001 0.09000000000000043
MSE= 0.046666666666666835
w= 2.2
1.0 2.0 2.2 0.04000000000000007
2.0 4.0 4.4 0.16000000000000028
3.0 6.0 6.6000000000000005 0.36000000000000065
MSE= 0.18666666666666698
w= 2.3000000000000003
1.0 2.0 2.3000000000000003 0.09000000000000016
2.0 4.0 4.6000000000000005 0.36000000000000065
3.0 6.0 6.9 0.8100000000000006
MSE= 0.42000000000000054
w= 2.4000000000000004
1.0 2.0 2.4000000000000004 0.16000000000000028
2.0 4.0 4.800000000000001 0.6400000000000011
3.0 6.0 7.200000000000001 1.4400000000000026
MSE= 0.7466666666666679
w= 2.5
1.0 2.0 2.5 0.25
2.0 4.0 5.0 1.0
3.0 6.0 7.5 2.25
MSE= 1.1666666666666667
w= 2.6
1.0 2.0 2.6 0.3600000000000001
2.0 4.0 5.2 1.4400000000000004
3.0 6.0 7.800000000000001 3.2400000000000024
MSE= 1.6800000000000008
w= 2.7
1.0 2.0 2.7 0.49000000000000027
2.0 4.0 5.4 1.960000000000001
3.0 6.0 8.100000000000001 4.410000000000006
MSE= 2.2866666666666693
w= 2.8000000000000003
1.0 2.0 2.8000000000000003 0.6400000000000005
2.0 4.0 5.6000000000000005 2.560000000000002
3.0 6.0 8.4 5.760000000000002
MSE= 2.986666666666668
w= 2.9000000000000004
1.0 2.0 2.9000000000000004 0.8100000000000006
2.0 4.0 5.800000000000001 3.2400000000000024
3.0 6.0 8.700000000000001 7.290000000000005
MSE= 3.780000000000003
w= 3.0
1.0 2.0 3.0 1.0
2.0 4.0 6.0 4.0
3.0 6.0 9.0 9.0
MSE= 4.666666666666667
w= 3.1
1.0 2.0 3.1 1.2100000000000002
2.0 4.0 6.2 4.840000000000001
3.0 6.0 9.3 10.890000000000004
MSE= 5.646666666666668
w= 3.2
1.0 2.0 3.2 1.4400000000000004
2.0 4.0 6.4 5.760000000000002
3.0 6.0 9.600000000000001 12.96000000000001
MSE= 6.720000000000003
w= 3.3000000000000003
1.0 2.0 3.3000000000000003 1.6900000000000006
2.0 4.0 6.6000000000000005 6.7600000000000025
3.0 6.0 9.9 15.210000000000003
MSE= 7.886666666666668
w= 3.4000000000000004
1.0 2.0 3.4000000000000004 1.960000000000001
2.0 4.0 6.800000000000001 7.840000000000004
3.0 6.0 10.200000000000001 17.640000000000008
MSE= 9.14666666666667
w= 3.5
1.0 2.0 3.5 2.25
2.0 4.0 7.0 9.0
3.0 6.0 10.5 20.25
MSE= 10.5
w= 3.6
1.0 2.0 3.6 2.5600000000000005
2.0 4.0 7.2 10.240000000000002
3.0 6.0 10.8 23.040000000000006
MSE= 11.94666666666667
w= 3.7
1.0 2.0 3.7 2.8900000000000006
2.0 4.0 7.4 11.560000000000002
3.0 6.0 11.100000000000001 26.010000000000016
MSE= 13.486666666666673
w= 3.8000000000000003
1.0 2.0 3.8000000000000003 3.240000000000001
2.0 4.0 7.6000000000000005 12.960000000000004
3.0 6.0 11.4 29.160000000000004
MSE= 15.120000000000005
w= 3.9000000000000004
1.0 2.0 3.9000000000000004 3.610000000000001
2.0 4.0 7.800000000000001 14.440000000000005
3.0 6.0 11.700000000000001 32.49000000000001
MSE= 16.84666666666667
w= 4.0
1.0 2.0 4.0 4.0
2.0 4.0 8.0 16.0
3.0 6.0 12.0 36.0
MSE= 18.666666666666668
可以显而易见
w= 2.0
1.0 2.0 2.0 0.0
2.0 4.0 4.0 0.0
3.0 6.0 6.0 0.0
MSE= 0.0
当w=2时,mse=0,即我们需要的最优模型为y=2x
绘图显示如下:
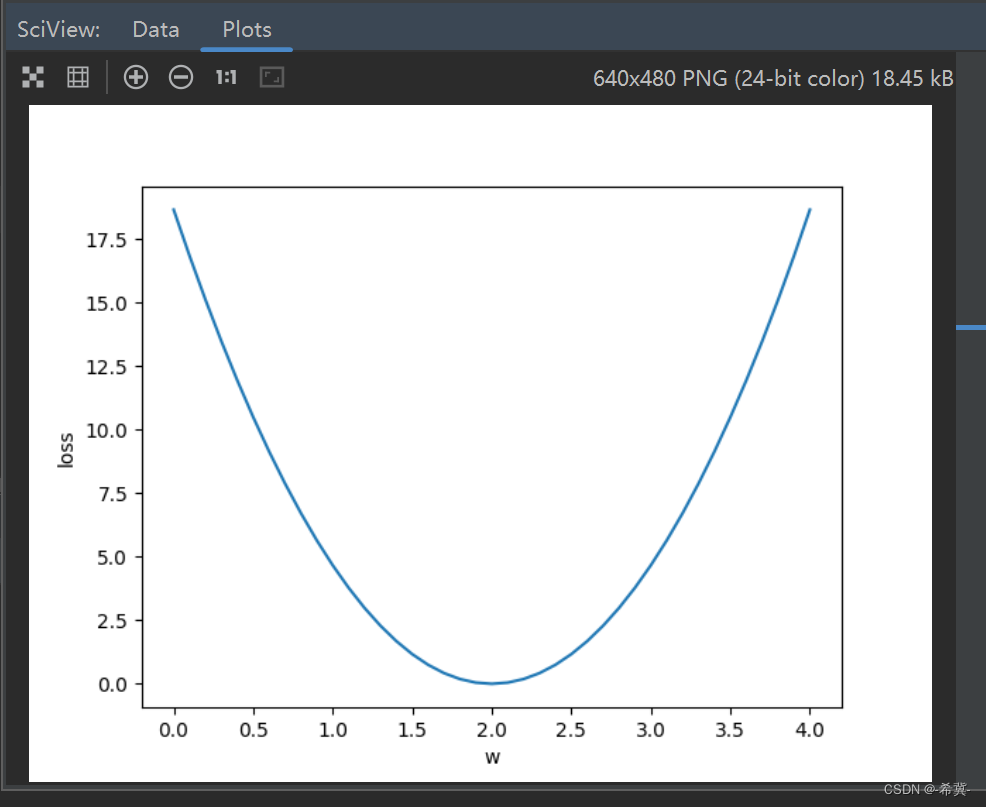
从图上也可以直观显示w=2时模型为优。
二、示例代码解读
1.线性回归模型
在这个示例代码中,定义了一个简单的线性回归模型,其中输入特征与权重参数进行线性组合,得到预测结果。这个模型的数学表示就是y=w*x,其中y是预测结果,w是权重参数,x是输入特征。
2.MSE损失函数
使用最小均方误差MSE作为损失函数来衡量模型的拟合准确性。MSE计算预测值与真实值之差的平方,并求平均值。在这段代码中,定义了一个损失函数loss(x,y),其中x和y分别表示输入特征和真实值。该函数通过调用前向传播函数forward(x)得到预测值,并在计算损失时使用了MSE公式。
3.优化过程
现在,我们探讨优化过程。在代码中,我们使用了np.arange生成0.0到4.0步长为0.1的一系列权重值作为迭代的候选权重参数,然后,通过遍历数据集中样本,计算每个权重值对应的平均损失。循环迭代过程中,存储权重和损失值的列表w_list和mse_list,最终使用matplotlib.pyplot绘制出权重与平均损失的关系图。
4.结果解读
通过绘制的图像,我们可以观察到权重与平均损失之间的关系。对于不同的权重取值,平均损失会有所变化。我们的目的是寻找使损失最小化的最优权重。通过不断调整权重参数,我们可以优化模型的拟合效果,使得预测结果与真实值更接近。
关于文章中zip()函数用法,可以参看我的这一篇文章:Python中的zip函数:合并和解压可迭代对象的利器。
总结
通过观察权重与平均损失的关系图,我们可以找到使损失最小化的最优权重。这个示例代码展示了如何利用线性回归模型和MSE损失函数来优化权重参数,以实现更好的数据拟合。线性回归是机器学习中最基础的模型之一,理解其原理和应用对于理解其他回归算法和数据拟合技术非常重要。通过学习和应用这些基本概念,我们可以更好地处理和分析实际问题,并为数据提供准确的预测和解释。