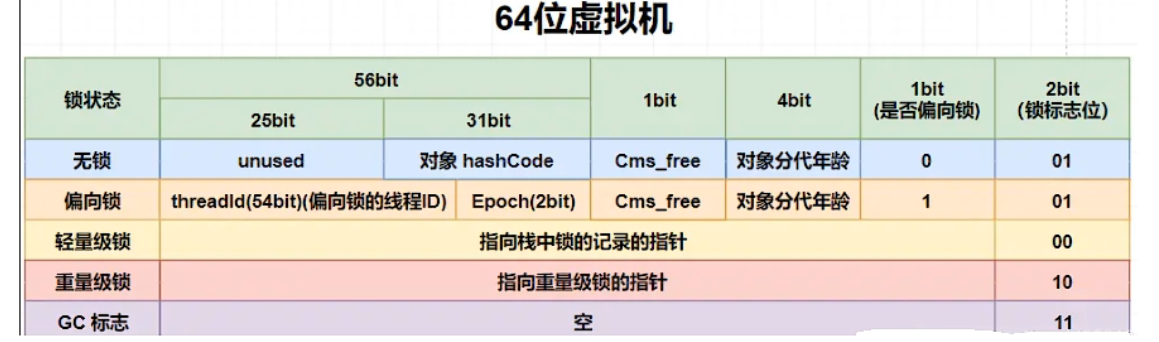
射频同轴线阻抗
射频同轴线的阻抗与线的绝缘介质的介电常数有关,与线的屏蔽层半径与内部导线半径的比值有关:
R
0
=
1
2
π
μ
′
ϵ
′
ln
(
r
2
r
1
)
\begin{align} R_0=\frac{1}{2\pi}\sqrt{\frac{\mu^{'}}{\epsilon^{'}}}\ln(\frac{r_2}{r_1}) \end{align}
R0=2π1ϵ′μ′ln(r1r2)
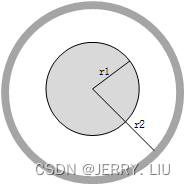
式中,
r
1
r_1
r1为同轴线内芯导线的半径,
r
2
r_2
r2为同轴线外层屏蔽层的半径,内芯导线与屏蔽层之间的绝缘介质的介电常数为
ϵ
′
\epsilon^{'}
ϵ′,磁导率为
μ
′
\mu^{'}
μ′.
由公式可知,同轴线绝缘介质的介电常数越大,单位长度的阻抗越小;外径与内径之比
r
2
r
1
\frac{r_2}{r_1}
r1r2越大,阻抗越大。
绝缘层的介电常数
μ
′
\mu^{'}
μ′与磁导率
ϵ
′
\epsilon^{'}
ϵ′与单位长度的电感
L
0
L_0
L0、单位长度的电容
C
0
C_0
C0之间有以下关系:
μ
′
ϵ
′
=
L
0
C
0
\begin{align} \mu^{'}\epsilon^{'}=L_0C_0 \end{align}
μ′ϵ′=L0C0
单位长度同轴线的电感
同轴线的电感为内自感与外自感之和,内自感为磁链与部分电流相交链形成的电感,外电感为磁链与全部电流相交链形成的电感;
根据安培环路定律可以计算同轴线单位长度的电感量. 安培环路定律:
∮
H
d
l
=
I
\begin{align} \oint H dl =I \end{align}
∮Hdl=I
同轴线单位长度的内自感
L
i
L_{i}
Li为:
L
i
=
μ
0
8
π
\begin{align} L_{i}=\frac{\mu_0}{8\pi} \end{align}
Li=8πμ0
μ
0
\mu_0
μ0为同轴线缆的内芯线的磁导率.
同轴线单位长度的外自感
L
o
L_{o}
Lo为:
L
o
=
μ
′
2
π
ln
(
r
2
r
1
)
\begin{align} L_o=\frac{\mu^{'}}{2\pi}\ln(\frac{r_2}{r_1}) \end{align}
Lo=2πμ′ln(r1r2)
同轴线单位长度的电感
L
0
L_0
L0为同轴线单位长度的内自感与同轴线单位长度的外自感之和:
L
0
=
L
i
+
L
o
=
μ
0
8
π
+
μ
′
2
π
ln
(
r
2
r
1
)
\begin{align} L_0&=L_i+L_o\\ &=\frac{\mu_0}{8\pi}+\frac{\mu^{'}}{2\pi}\ln(\frac{r_2}{r_1}) \end{align}
L0=Li+Lo=8πμ0+2πμ′ln(r1r2)
内自感的值相比外自感较小,可以忽略而只考虑外自感,即
L
0
=
μ
′
2
π
ln
(
r
2
r
1
)
\begin{align} L_0=\frac{\mu^{'}}{2\pi}\ln(\frac{r_2}{r_1}) \end{align}
L0=2πμ′ln(r1r2)
单位长度同轴线的电容
利用高斯定律,可以计算同轴线缆单位长度的电容。高斯定律的表述为:电位移矢量
D
D
D在闭合曲面
S
S
S上的通量为闭合曲面内部电荷量
q
q
q,公式为:
∮
D
d
S
=
q
\begin{align} \oint D dS = q \end{align}
∮DdS=q
绝缘介质内的电场强度
E
E
E的方向为同轴线截面内由中心发出的径向方向
ϵ
′
E
2
π
ρ
l
=
q
E
=
q
2
π
ρ
l
ϵ
′
U
=
∫
r
1
r
2
E
d
ρ
=
q
2
π
l
ϵ
′
ln
(
r
2
r
1
)
C
=
q
U
=
2
π
l
ϵ
′
ln
(
r
2
r
1
)
C
0
=
2
π
ϵ
′
ln
(
r
2
r
1
)
\begin{align} \epsilon^{'}E2\pi \rho l =q\\ E=\frac{q}{2\pi\rho l \epsilon^{'}}\\ U=\int_{r1}^{r2} Ed\rho = \frac{q}{2\pi l \epsilon^{'}}\ln(\frac{r_2}{r_1})\\ C=\frac{q}{U}=\frac{2\pi l \epsilon^{'}}{\ln(\frac{r_2}{r_1})}\\ C_0=\frac{2\pi \epsilon^{'}}{\ln(\frac{r_2}{r_1})}\\ \end{align}
ϵ′E2πρl=qE=2πρlϵ′qU=∫r1r2Edρ=2πlϵ′qln(r1r2)C=Uq=ln(r1r2)2πlϵ′C0=ln(r1r2)2πϵ′
因此同轴线单位长度的电容
C
0
C_0
C0为
C
0
=
2
π
ϵ
′
ln
(
r
2
r
1
)
\begin{align} C_0=\frac{2\pi \epsilon^{'}}{\ln(\frac{r_2}{r_1})} \end{align}
C0=ln(r1r2)2πϵ′
同轴线缆阻抗的计算
同轴线缆阻抗
R
0
R_0
R0为
R
0
=
L
0
C
0
=
1
2
π
μ
′
ϵ
′
ln
(
r
2
r
1
)
=
1
2
π
μ
r
ϵ
r
μ
0
ϵ
0
ln
(
r
2
r
1
)
\begin{align} R_0 &= \sqrt{\frac{L_0}{C_0}}\\ &=\frac{1}{2\pi}\sqrt{\frac{\mu^{'}}{\epsilon^{'}}}\ln(\frac{r_2}{r_1})\\ &=\frac{1}{2\pi}\sqrt{\frac{\mu_r}{\epsilon_r}}\sqrt{\frac{\mu_0}{\epsilon_0}}\ln(\frac{r_2}{r_1}) \end{align}
R0=C0L0=2π1ϵ′μ′ln(r1r2)=2π1ϵrμrϵ0μ0ln(r1r2)
真空磁导率
μ
0
=
4
π
∗
1
0
−
7
\mu_0=4\pi*10^{-7}
μ0=4π∗10−7 H/m, 介电常数
ϵ
0
=
1
36
π
∗
1
0
−
9
\epsilon_0=\frac{1}{36\pi}*10^{-9}
ϵ0=36π1∗10−9 F/m, 因此
μ
0
ϵ
0
=
120
π
Ω
\begin{align} \sqrt{\frac{\mu_0}{\epsilon_0}}=120\pi \Omega \end{align}
ϵ0μ0=120πΩ
真空、电介质等材料为非磁材料,其相对磁导率
μ
r
\mu_r
μr约为1, 因此,结合(19),式子(18)可写为:
R
0
=
1
2
π
μ
r
ϵ
r
μ
0
ϵ
0
ln
(
r
2
r
1
)
=
60
μ
r
ϵ
r
ln
(
r
2
r
1
)
=
60
ϵ
r
ln
(
r
2
r
1
)
\begin{align} R_0 &=\frac{1}{2\pi}\sqrt{\frac{\mu_r}{\epsilon_r}}\sqrt{\frac{\mu_0} {\epsilon_0}}\ln(\frac{r_2}{r_1})\\ &=60\sqrt{\frac{\mu_r}{\epsilon_r}}\ln(\frac{r_2}{r_1})\\ &=\frac{60}{\sqrt{\epsilon_r}}\ln(\frac{r_2}{r_1}) \end{align}
R0=2π1ϵrμrϵ0μ0ln(r1r2)=60ϵrμrln(r1r2)=ϵr60ln(r1r2)